
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основы теории оболочек вращенияСтр 1 из 7Следующая ⇒ Оболочка - тонкостенная конструкция, с постоянной толщиной.
Основным геометрически понятием теории оболочек постоянной толщины являются понятия срединной поверхности и слоя оболочки. Срединной или средней поверхностью оболочки называется поверхность, равноудалённая от её внутренней и наружной поверхностей.
Безмоментную оболочку можно рассматривать как приближённую модель реальной оболочки, если в последней не учитывать изгибающие и крутящие моменты.
Обозначим Внешние нагрузки, действующие на оболочку, отнесённые к площади элемента срединной поверхности , обозначим так: Площадь элемента Так как
Сокращая на величину
Но
следовательно, разделив уравнение (2) на величину r, получим
Второе уравнение равновесия в тангенциальной плоскости удобнее всего получить, взяв сумму моментов всех сил относительно точки 
сократив на величину
Разделив уравнение (5) на величину arи учитывая тождества (3) получим
Третье уравнение равновесия получим, составив сумму проекций всех сил на направление внутренней нормали к поверхности. Силы
Разделив это уравнение на
Уравнения (4),(6),(7)являются искомыми уравнениями равновесия элемента безмоментной оболочки вращения. Силы Для изотропной упругой оболочки с учётом температурного расширения
Здесь Е иG - соответственно модуль Юнга и модуль сдвига материала оболочки; Система уравнений будет полной, если добавить ранее полученные выражения деформаций через перемещения
Через перемещение
Отличительной чертой полученных уравнений является то, что они допускают раздельное интегрирование. Интегрируя уравнения (4),(6),(7), можно найти общие выражения для сил При расчёте оболочки по безмоментной теории принципиально важна правильная формулировка граничных условий. Анализ полной системы уравнений показывает, что в безмоментной теории оболочек на каждом торце можно задавать только два тангенциальных граничных условия, в которые могут входить либо тангенциальные силы |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 573. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
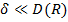
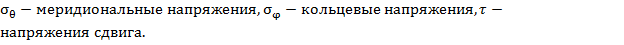 Эти напряжения равномерно распределённые по толщине h. Вместо напряжений можно рассматривать погонные силы
Эти напряжения равномерно распределённые по толщине h. Вместо напряжений можно рассматривать погонные силы 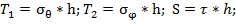 действующие в срединной поверхности.
действующие в срединной поверхности.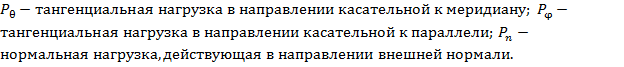
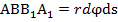 . Внешние силы
. Внешние силы 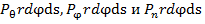 производят работу на перемещениях
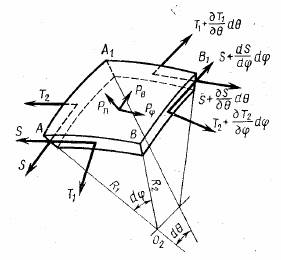
производят работу на перемещениях 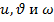 соответственно. Чтобы составить уравнения равновесия в тангенциальной плоскости, надо рассмотреть равновесие плоской трапеции
соответственно. Чтобы составить уравнения равновесия в тангенциальной плоскости, надо рассмотреть равновесие плоской трапеции 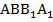 с углом
с углом 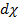 между направлениями
между направлениями 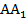 и
и 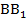 . Длины сторон АВ,
. Длины сторон АВ, 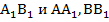 трапеции соответственно равны
трапеции соответственно равны 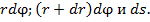
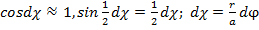 то, проектируя все силы на ось, перпендикулярную сторонам АВ и
то, проектируя все силы на ось, перпендикулярную сторонам АВ и 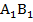 трапеции, получим
трапеции, получим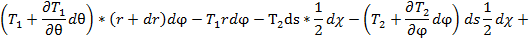
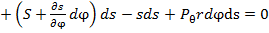 (1)
(1)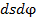 и полагая в соответствии с правилами дифференциального исчисления
и полагая в соответствии с правилами дифференциального исчисления 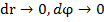 получаем
получаем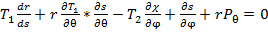 (2)
(2)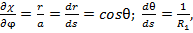 (3)
(3)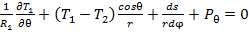 (4)
(4) пересечения сторон
пересечения сторон 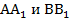 трапеции.
трапеции.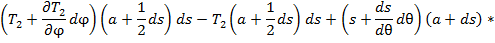
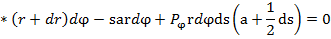
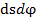 и полагая
и полагая 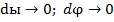 , найдём
, найдём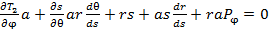 (5)
(5)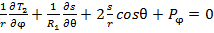 (6)
(6)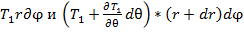 лежат в плоскости меридиана и угол между ними составляет
лежат в плоскости меридиана и угол между ними составляет 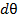 . С точностью до величины второго порядка малости силы
. С точностью до величины второго порядка малости силы 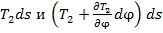 лежат в нормальной плоскости
лежат в нормальной плоскости 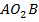 и угол между ними равен
и угол между ними равен 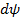 . Сумма проекций всех сил на нормаль с требуемой точностью будет определена по зависимости
. Сумма проекций всех сил на нормаль с требуемой точностью будет определена по зависимости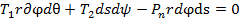
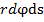 , с учётом предыдущих выражений получим
, с учётом предыдущих выражений получим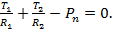 (7)
(7)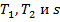 связаны законом Гука с деформациями
связаны законом Гука с деформациями  срединной поверхности.
срединной поверхности.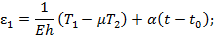
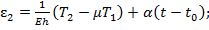 (8)
(8)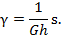
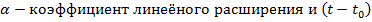 приращение температуры в срединной поверхности оболочки.
приращение температуры в срединной поверхности оболочки.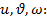
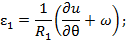
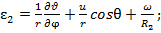 (9)
(9)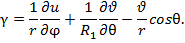
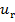 вдоль радиуса rудлинение
вдоль радиуса rудлинение 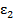 выражается формулой
выражается формулой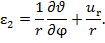
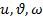 интегрируя уравнения (9).
интегрируя уравнения (9).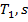 либо тангенциальные перемещения
либо тангенциальные перемещения 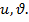 Может существовать комбинация величин
Может существовать комбинация величин 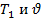 или sи u, и невозможно рассматривать условия
или sи u, и невозможно рассматривать условия 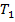 одновременно с u, так же как sc
одновременно с u, так же как sc 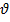 . Граничные условия по
. Граничные условия по 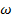 можно удовлетворить, рассматривая моментную теорию оболочек.
можно удовлетворить, рассматривая моментную теорию оболочек.