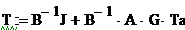Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
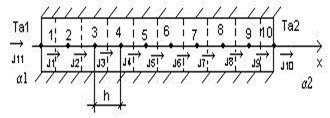
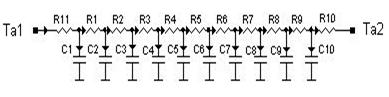
Нестационарный процесс распределения температур в однородном стержневом элементеРассмотрим одномерныйстержневой элемент, теплоизолированный с боковой поверхности. Поперечное сечение стержня мало, поэтому можно пренебречь изменением температуры по его сечению. В этом случае, температурное поле стержня является одномерным и изменяется только по оси x, направленной по длине стержня. Постановка задачи. Зададим граничные условия 3 рода, т.е. на границах стержня происходит теплообмен со средой. Для решения задачи примем следующие начальные данные: · материал стержня – сталь; · температура среды и коэффициент теплоотдачи со стороны левой границы стержня равны: Та1=100 0С и α1=4000 Вт/м2 0С, со стороны правой – Та2=200С и α2=500 Вт/м2 0С; · длина стержня L = 0,09 м; · коэффициент теплопроводности материала стержня λ = 50 Вт/м 0С; · площадь поперечного сечения A = 3,14∙10-4 м2; · плотность стали ρ = 7800 кг/м3; · теплоемкость с=460 Дж/кг0С; · расстояние h между узлами равно 0,01 м. Решение задачи. Разобьем длину стержня сечениями перпендикулярными оси x на 10 конечных объемов длиной h=0.01м. Соответствующая тепловая схема приведена на рис.3.9. В центре каждого объема поместим по одному узлу, при этом номер узла совпадает с номером объема. Пронумеруем узлы тепловой схемы так, как показано на рис.3.9 от узла 1 (на левом торце стержня) до узла 10 (на правом торце стержня). а)
б) Рисунок 8. Стержень, теплоизолированный с боковой поверхности (а) и его тепловая схема (б) Составим матрицу инциденции A, которая в рассматриваемом примере имеет размерность 10*11:
 Матрица проводимостей (36) G имеет размерность 11*11, является диагональной:
Матрица теплоемкостей C имеет размерность 10*10, является диагональной и ее диагональные элементы равны:
где A – площадь сечения стержня, м2; ρ – плотность стали, кг/м3; с – теплоемкость стали; h – расстояние между границами объема, м. Строим матрицу C:
Вектор-столбец Ta известных температур среды равен:
Матрично-топологическое уравнение тепловой схемы относительно вектора неизвестных температур в узлах схемы имеет вид: Уравнение (41) является матричным дифференциальным уравнением в обыкновенных производных и описывает нестационарные температуры в узлах тепловой схемы. Примем начальные температуры в узлах равными 00С, т.е. Рассмотрим решение нестационарного матричного уравнения
где H(t) – положительно определенная матрица для всех t ≥ 0 и равна
с начальным условием T(0)=T0, (43) Для решения нестационарного матричного уравнения (41) с начальным условием (43) используем явный метод Эйлера. Явный метод Эйлера приводит к итерационной процедуре:
где m – номер итерации; τ – шаг по времени; E – диагональная единичная матрица. Диагональная единичная матрица E, имеющая размерность 10*10 равна
В явном методе Эйлера значение вектора-столбца температуры Tm в следующий момент времени tm находится пересчетом по формуле (44) на основании известного значения температуры Tm-1 в предыдущий момент времени tm-1. Зададим дополнительные условия для решения задачи: 4) шаг по времени τ = 2; 5) максимальное время M = 100 с.; 6) условие m…M. Подставив все известные величины в уравнение (44), найдем температуры в узлах через 1с., 40с., и 100 с.:
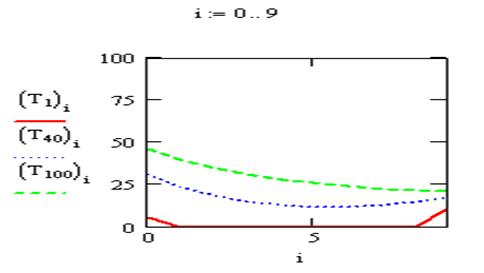
Рисунок 9. График зависимости температуры от безразмерной координаты в моменты времени через 1, 40 и 100 с.
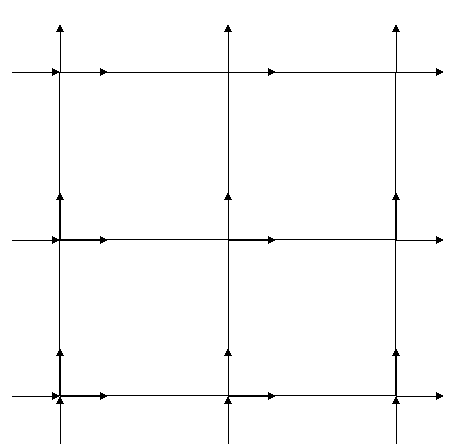
9. Двумерная пластина с теплообменом с поверхности в среду Рассмотрим двумерную пластину, пренебрегем изменением температуры по ее толщине. В этом случае, температурное поле пластины является двумерным и изменяется только по оси х и у. Зададим граничные условия 3 рода, т.е. на границах пластины происходит теплообмен со средой. Для решения задачи примем следующие начальные данные: · температуры сред и коэффициенты теплоотдачи со сторон границ пластины соответственно равны: Та1=400 0С, Та2=50 0С, Та3=500 0С, Та4=60 0С,α1=3000 Вт/м2 0С, α2=60 Вт/м2 0С, α3=100 Вт/м2 0С, α4=2000 Вт/м2 0С; · длина пластины L равна 80 мм; · теплопроводности материалов λ1 = 50 Вт/м 0С, λ2 =30 Вт/м 0С, λ3 = 390 Вт/м 0С, λ4 = 400 Вт/м 0С; · А0=0.0004 м2 ;
а) Та4 У4 У7 У10
У1 1 У2 2 У5 3 У8
R1 R2
R3 R4 R5 λ1 λ3
б)
g1 g2 g5 g8
g3 g6 g9 g12 g14 g11 g16
g18 g19 g21 g23
g20 g22 g24
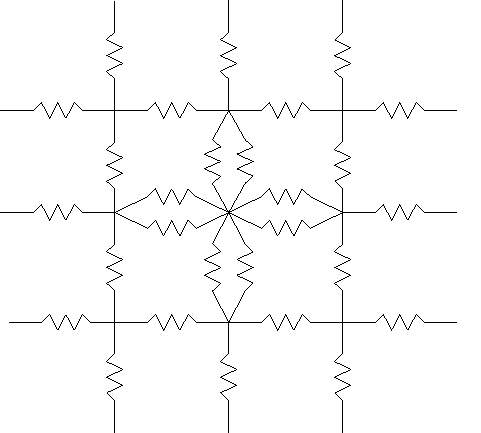
Рисунок 4. Двумерная пластина (а) и ее тепловая схема (б) Рассмотрим баланс потока теплоты в i-ом выделенном объеме, воспользовавшись интегральным уравнением теплового баланса
где Vi = A∆xi – объем i-го элемента; Si- площадь всей поверхности выделенного i -го объема. Индекс i относит рассматриваемые переменные к i-му выделенному объему. Поверхностный интеграл в левой части уравнения (3.3.1) выражает суммарный тепловой поток, пересекающий поверхность выделенного i-ro объема. Так как, рассматриваемая задача является стационарной, т.е. dT/dt =0 Уравнения теплового баланса, записанные для узлов тепловой схемы, имеют вид:
где R – тепловые сопротивления выделенных объемов между узлами и рассчитываются А на границе материалов тепловые сопротивления рассчитываются как Конвективные тепловые проводимости, которые входят в ветви Соответственно тепловые проводимости равны g1=1.2; g2=0.5; g3=0.5; g4=0.024; g5=0.3; g6=0.4; g7=0.024; g8=0.04; g9=0.3; g10=0.024; g11=1.2; g12=2.2; g13=3.9; g14=1.15; g15=2.95; g16=0.04; g17=2; g18=1.2; g19=3.9; g20=0.8; g21=2; g22=0.8; g23=0.04; g24=0.8 В стационарном случае, вектор-столбец температур Т описывается матричным уравнением, при
Введя вектор-столбец тепловых потоков ветвей J=||J1 J2 J3 J4 J5 …… J24||Т, систему уравнений можно записать в матричном виде AJ=0 (22) Матрица A называется матрицей инциденций, для рассматриваемого случая имеет размерность 9*24 и равна:
Она получается путем сложения по горизонтали отдельных матриц в программе MathCAD с помощью функции augment
АТ – транспонированная матрица А
Уравнение (22) является, по существу, дискретным уравнением баланса тепловых потоков в тепловой схеме. Вид матрицы A нетрудно понять. Строки матрицы соответствуют узлам графа, а столбцы матрицы соответствуют ветвям графа, причем номер столбца равен номеру ветви в тепловой схеме. Разности температур в ветвях графа можно представить в виде вектора- столбца ΔT:
.
Введя вектор столбец температур узлов графа
Простым перемножением легко убедится, что вектор-столбец (3.3.6) можно записать в следующем матричном виде:
где Та - вектор-столбец известных температур в ветвях. Сравнение матрицы инциденций A и матрицы в соотношении (23) показывает, что последняя матрица является транспонированной по отношению к матрице А, т.е. равна ΔТ=АТТ (26)
Полученные матрично-топологические соотношения (3.3.4) и (3.3.8) устанавливают связь между тепловыми потоками в ветвях тепловой схемы и преобразование узловых температур в разности температур в ветвях. Матрица инциденций А отображает структуру тепловой схемы. Матрица А, естественным образом, была получена из системы уравнений баланса тепловых потоков в узлах графа. Для исчерпывающего описания графа тепловой схемы необходимо располагать соотношениями, связывающими тепловые потоки и разности температур в ветвях графа, в соответствии с элементами схемы, представленными ветвями. Выше было показано, что тепловой поток Ji в i-ой ветви равен Ji=giΔTi. Тогда связь векторов-столбцов J и ΔТ может быть записана в следующем матричном виде: где G – квадратная матрица проводимостей ветвей размерностью М*М, М – количество ветвей графа. Матрица проводимостей G формируется следующим образом: если ветвь i представляет собой тепловую проводимость gi (кондуктивную или конвективную), то элемент ii матрицы G равен gi. Строим матрицу проводимостей G:
Она получается путем сложения по горизонтали отдельных матриц в программе MathCAD с помощью функции augment и сложения по вертикали с помощью функции stack. Строим новую матричную функцию:
(28)
(29) Подставляя в уравнение (29) находим искомые температуры в узлах стержневого элемента
Т1=402.2530С Т2=399.6650С Т3=379.6520С Т4=426.6760С Т5=431.8190С Т6=429.1660С Т7=435.1150С Т8=441.0480С Т9=442.650С
Рисунок 5. График распределения температур полученный в программе MathCAD |
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 293. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
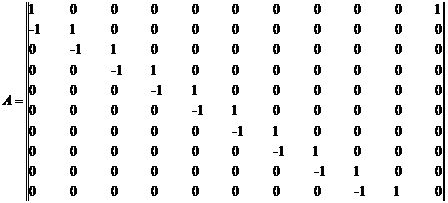 (36)
(36) 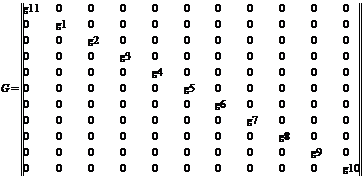 (37)
(37)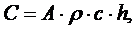 , (38)
, (38) (39)
(39) (40)
(40)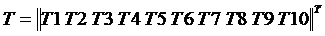
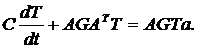 (41)
(41)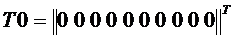
 (42)
(42) ;
;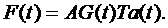
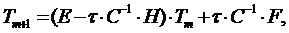 (44)
(44)
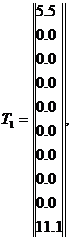

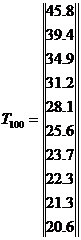 .
.
 g13 g15 g17
g13 g15 g17  (20)
(20)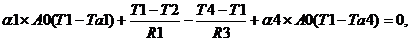

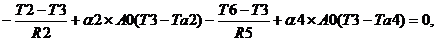






 и соответствуют кондуктивной проводимости
и соответствуют кондуктивной проводимости ,где λi и λg-коэффициенты теплопроводности граничащих материалов.
,где λi и λg-коэффициенты теплопроводности граничащих материалов. .
. , т.е.
, т.е. (21)
(21)



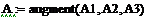

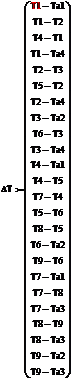
 (23)
(23)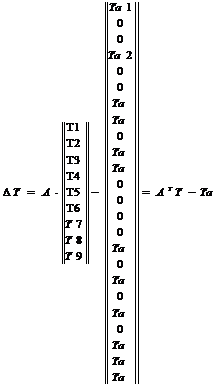 (24)
(24) (25)
(25) (27)
(27)

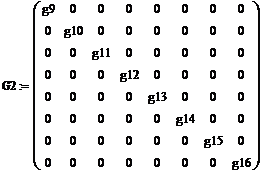









 -вектор –столбец начальных температур в момент времени равный нулю в узлах тепловой схемы.
-вектор –столбец начальных температур в момент времени равный нулю в узлах тепловой схемы.