
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формальное решение логических задач.
Билет №7 Алгебра логики. Основные законы алгебры логики. Алгебра переключательных схем.
Законы алгебры логики Для логических величин обычно используются три операции: • Конъюнкция – логическое умножение (И) – and, &, ∧. • Дизъюнкция – логическое сложение (ИЛИ) – or, |, v. • Логическое отрицание (НЕ) – not, . Логические выражения можно преобразовывать в соответствии с законами алгебры логики: 1. Законырефлексивности: a∨a = a a∧a = a 2. Законы коммутативности: a ∨ b = b ∨ a a ∧ b = b ∧ a 3. Законы ассоциативности: (a∧ b) ∧ c = a ∧ (b ∧ c) (a∨ b) ∨ c = a ∨ (b ∨ c) 4. Законы дистрибутивности: a ∧ (b ∨ c) = a ∧ b ∨ a ∧ c a ∨ b ∧ c = (a ∨ b) ∧ (a ∨ c) 5. Закон отрицания отрицания: ( a) = a 6. Законы де Моргана: (a ∧ b) = a ∨ b (a ∨ b) = a ∧ b 7. Законыпоглощения: a ∨ a ∧ b = a a ∧ (a ∨ b) = a
Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.  Переключательными принято называть схемы устройств, содержащих двухпозиционные переключатели, т. е пребывающие в одном из двух возможных состояний. В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. При разработке схем используется аппарат алгебры логики. Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает • значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; • если же переключатель разомкнут, то х равен нулю Будем считать, что два переключателя Х и ⌐Х связаны таким образом, что когда Х замкнут, то ⌐Х разомкнут, и наоборот. Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.
Билет №8. Булевы функции. Существование ограниченного числа функций от n переменных. Булевы функции двух переменных. Полные системы булевых функций. Возможность выражения любых булевых функций через полную систему.
Существует ровно Для n = 2 существует 16 различных булевых функций.
Множество Критерий Поста формулирует необходимое и достаточное условие полноты системы булевых функций: Широко известны такие полные системы булевых функций:
Билет №9.Канонические формы логических формул. Элементарная конъюнкция. Дизъюнктивная нормальная форма (ДНФ). Совершенная ДНФ (СДНФ). Теорема о существовании СДНФ.
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 1310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  ,......,
,......,  ), аргументы которой
), аргументы которой 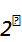 различных бинарных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, то общее количество различных булевых функций от n аргументов равно
различных бинарных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, то общее количество различных булевых функций от n аргументов равно 

 функций алгебры логики называется полной системой, если замыкание(Замкнутый класс в теории булевых функций — такое множество P функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: [P]=P. Другими словами, любая функция, которую можно выразить формулой с использованием функций множества P, снова входит в это же множество) этого множества совпадает с множеством всех функций. (В частности, для двузначной логики
функций алгебры логики называется полной системой, если замыкание(Замкнутый класс в теории булевых функций — такое множество P функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: [P]=P. Другими словами, любая функция, которую можно выразить формулой с использованием функций множества P, снова входит в это же множество) этого множества совпадает с множеством всех функций. (В частности, для двузначной логики  .) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества
.) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества  ,
, 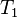 ,
,  ,
,  ,
,  .
. (конъюнкция, дизъюнкция, отрицание);
(конъюнкция, дизъюнкция, отрицание); (конъюнкция, сложение по модулю 2, константа 1);
(конъюнкция, сложение по модулю 2, константа 1); (конъюнкция, отрицание);
(конъюнкция, отрицание); (дизъюнкция, отрицание);
(дизъюнкция, отрицание); (стрелка Пирса);
(стрелка Пирса); (штрих Шеффера).
(штрих Шеффера).