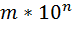Целочисленное переполнение.

Целочисленное переполнение происходит когда мы пытаемся записать в переменную значение, большее максимального значения типа этой переменной.

(Пример для понимания сути происходящего)

Обьявим две переменные A и B, типа UnsignedInteger. Далее занесем в А максимальное значение UnsignedInteger - 4294967295, а в В -1:

unsignedint A=0xFFFFFFFF;

unsignedint B=0x1;

В результате выполнения операции (А+В) полученное значение, согласно стандарту ISO, не вмещается в 32 бита. В таком случае результатом будет (А+В) mod 0x100000000. mod - остаток от деления, например (8 mod 2 =0), а (8 mod 3=2). Следовательно, наш результат будет равен выражению:

result=(A+B) % 0x100000000;

подставив наши значения получим следующее:

result=(0xffffffff + 0x1) % 0x100000000;

//result=(0x100000000) % 0x100000000;

//result=0;

Как видно результат вышел равен нулю. Не совсем то, что должно было выйти :) Этот эффект называют "wraparound", тоесть вращение вокруг нуля.

Билет №4.Особенности представления информации в компьютере. Представление вещественных чисел. Нормализованная запись числа. Формат с плавающей запятой. Мантисса и порядок. Выполнение операций над числами в формате с плавающей запятой. Потеря точности. Переполнение чисел с плавающей запятой.

Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.

Число с плавающей запятой (или число с плавающей точкой) — форма представления вещественных (действительных) чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную.

В нормализованной записи числа мантисса десятичного числа принимает значения от 1 (включительно) до 10 (не включительно), а мантисса двоичного числа принимает значения от 1 (включительно) до 2 (не включительно). В такой форме любое число (кроме 0) записывается единственным образом. Недостаток заключается в том, что в таком виде невозможно представить 0, поэтому представление чисел в информатике предусматривает специальный признак (бит) для числа 0.

Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (понятно, что такое), порядок и мантиссу.

Число, записанное в стандартной форме, имеет вид

Число m называется мантиссой числа, записанного в стандартной форме.

Число n является целым числом (положительным, отрицательным или нулем) называется порядком числа, записанного в стандартной форме.В компьютерной записи вещественных чисел с плавающей запятой количество цифр, отводимых под запись порядка, определяет, насколько большие и насколько маленькие положительные числа могут быть представлены.

Например, число 3251 в стандартной форме записывается так:

Здесь число 3,251 является мантиссой, а число 3 является порядком.

Для чисел с плавающей запятой выполняются операции сложения, вычитания, деления и умножения.

Потеря точности:

Самая опасная операция с точки зрения округления в арифметике с плавающей запятой — это вычитание. При вычитании близких чисел значимые разряды могут потеряться, что может в разы увеличить относительную погрешность.

Неассоциативность арифметических операций.

В арифметике с плавающей запятой правило (a*b)*c = a*(b*c) не выполняется для любых арифметических операций. Например,

(1020+1)-1020=0 ≠ (1020-1020)+1=1

Не все десятичные числа имеют двоичное представление с плавающей запятой. Например, число «0,2» будет представлено как «0,200000003» в одинарной точности. Соответственно, «0,2 + 0,2 ≈ 0,4». Абсолютная погрешность в отдельном

случае может и не высока, но если использовать такую константу в цикле, можем получить накопленную погрешность.

Ошибки при проверке на равенство.

Переполнение.

Для чисел с плавающей запятой определены несколько специальных значений, которые весьма непривычны для программистов, привыкших к целочисленным операциям. Так, если взять самое большое целое число и прибавить к нему единицу, произойдёт переполнение, и число станет отрицательным. Если же прибавить единицу к самому большому числу с плавающей запятой, то не произойдёт ровным счётом ничего; в результате мы получим то же самое число. Это явление объясняется ниже. Переполнения можно добиться, к примеру, умножив это число на два. Но результат будет несколько необычным — "число" Inf (от англ. infinity = бесконечность). Аналогичным образом можно получить отрицательную бесконечность — -Inf.

Билет №5.

Особенности представления информации в компьютере. Представление текстовой информации. Кодировка ASCII. Национальные однобайтовые кодировки. Особенности кодировок cp866, cp1251 и koi8-r. Кодировки Unicode. Кодировка UTF-8 как пример кодировки переменной длины.

На сегодняшнее время компьютеры способны обрабатывать числовую, текстовую, графическую, звуковую и видео информацию. Однако большинство существующих компьютеров способно хранить и обрабатывать только дискретную информацию. Следовательно, любой вид информации, подлежащий к обработке на ЭВМ необходимо закодировать в числовом виде.
Представление текстовой информации.
В случае текстовой информации, каждому символу сопоставляется
двоичное число, образуя таблицу кодировок символов. Существует различные стандарты кодировок: ASCII, UCS-2, UCS-4. Например, в таблице ASCII одним байтом кодируются 256 символов (включая управляющие символы). Согласно этой кодировке букве b соответствует код 01100010, о – 01101111, k – 01101011. И слово book записывается четырьмя байтами 01100010 01101111 01101111 01101011.
ASCII — American Standard Code for Information Interchange — американскийстандартныйкоддляобменаинформацией. ASCII представляет собой 8-битную кодировку для представления десятичных цифр, латинского и национального алфавитов, знаков препинания и управляющих символов. Нижнюю половину кодовой таблицы (0 — 127) занимают символы US-ASCII, а верхнюю (128 — 255) — разные другие нужные символы. Слово ASCII чаще употребляется в женском роде.
До развития Юникода, символы национальных алфавитов, в том числе и кириллицы, кодировались с помощью одного байта. Получалась так называемая расширенная таблица ASCII символов, где первая часть таблицы была неизменной и содержала буквы латинского алфавита и некоторые вспомогательные знаки, а во второй части (начиная с 128) располагались буквы национальных алфавитов.

Для кириллицы существовало несколько отображений символов на эту вторую часть таблицы, наиболее известными из которых были KOI-8, Windows 1251, cp866, ISO 8859-5
Что такое кодировка Unicode

Кодировка Unicode представляет собой схему кодировки символов, которая позволяет кодировать практически все алфавиты в виде одного набора символов. Кодировка Unicode позволяет компьютерам представлять текст для большинства систем письма в мире и обращаться с ним. Разработка кодировки Unicode поддерживается организацией UnicodeConsortium и кодифицируется как стандарт. Проще говоря, кодировка Unicode представляет собой систему, позволяющую каждому использовать любые другие алфавиты. Представьте себе, существует даже версия Unicodeклингонского языка. Кодировка UTF-8

Использование большой кодовой таблицы ставит перед нами очень неприятную проблему. Поскольку номера символов из таблицы UCS-4 требуют четырёх байт, текст, закодированный таким образом, становится в 4 раза длиннее. Это плата за большой выбор используемых символов. Это очень расточительно, но по-другому не получится, если кодировать каждый символ одним и тем же количеством байтов.

Есть и другая возможность, но она предполагает отказ от фиксированной длины символов (измеренной в байтах). Это кодировки с переменной длиной символа. Большое распространение получила кодировка UTF-8.

для того, чтобы дать полное и точное изложение того, что представляет собой код Unicode и как он работает; ее предназначение - объяснить, как использовать кодировку Unicode в Delphi 2009. В данной статье, первой из трех, будет объяснено, почему так важна кодировка Unicode, и как в Delphi будет реализован новый тип строки UnicodeString.

Билет №6. Алгебра логики. Понятие высказывания. Основные логические операции и их таблицы истинности. Формальное решение логических задач.