
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Інтерполяційна формула ЛагранжаНехай на відрізку [a, b] дані (n + 1) різних значень аргументу: x0, x1, ..., xn і відомі відповідні значення виразів f(x0) = y0, f(x1) = y1, . . ., f(xn) = yn. (1). Необхідно побудувати поліном Ln(x) ступеню не вище n, що має у заданих вузлах x0, x1, ..., xn ті ж значення, що і функція ƒ(х), тобто такі, де Ln(xi) = yi, де i = 0, 1, ..., n. Будемо шукати Ln(x) у вигляді: Ln(x)=l0(x)+ l1(x)+...+ ln(x), (6) де li(x) - поліном степеню n, до того ж Очевидно, що вимога (7) з урахуванням (6) забезпечує виконання умов інтерполяції. Так як шуканий поліном li(x) звертається в нуль в n точках x0,., xi - 1, xi + 1, ..., xn, то він має вигляд li(x) = Ci (x - x0) (x - x1)⋅.⋅(x - xi-1) (x - xi +1)⋅...⋅(x - xn) (8) де Сi - постійний коефіцієнт. Вважаючи у формулі (8) х = xi і враховуючи, що li(xi) = yi, отримаємо: yi = Ci (xi - x0)(xi - x1)⋅...⋅(xi - xi -1)(xi - xi +1)⋅...⋅(xi - xn).
Звідси Зауважимо, що ні один із множників не дорівнює нулю. Підставляючи Сі в (8), а також з урахуванням (6), остаточно маємо: Це і є інтерполяційна формула Лагранжа. Формулі (9) можна надати більш стислий вигляд, використовуючи позначення
Диференціюючи по х цей добуток, отримаємо:
Вважаючи х = хi (i = 0, 1, ..., n), отримаємо: П′n+1(хi)= (xi - x0)⋅.⋅(xi - xi -1) (xi - xi +1)⋅...⋅(xi - xn). (11) Підставляючи вираз (10) та (11) у формулу (9), отримаємо Приклад
Припустимо n = 1. Ясно, що ми маємо в цьому випадку дві точки і інтерполяційна формула Лагранжа дає рівняння прямої, що проходить через дві задані точки. Позначивши абсциси цих точок через a і b, отримаємо інтерполяційний поліном у вигляді 
Приймаємо n = 2. Тоді отримаємо рівняння параболи, що проходить через три точки. Якщо позначити x0 = a, x1 = b, x2 = c, то таш вираз має вигляд
Приклад Нехай задані значення: x0 = 1, x1 = 3, x2 = 7, x3 = 12 и y0 = 5,6, y1 = 6,7, y2 = 8,1, y3 = 10,3. Необхідно визначити значення невідомої функції для х = 6,5.
Для заданого випадку, коли ми маємо чотири значення функції, інтерполяційна формула Лагранжа представляється таким чином:
Після підстановки заданих значень у формулу Лагранжа отримаємо:
Визначимо значення функцій при х = 6,5:
Приклад Нехай задана інтерполяційна таблиця:
Необхідно побудувати інтерполяційний поліном Лагранжа. Рішення.
З (8) маємо:
Приклад Користуючись інтерполяційною формулою Лагранжа, скласти рівняння прямої, що проходить через точки Р0(х0, у0) и Р1(х1, у1), якщо х0=-1, у0=-3, х1=2, у1=4. Рішення. У даному випадку многочлен (поліном) Лагранжа прийме вигляд
Рівняння шуканої прямої є |
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 260. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
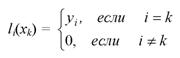 (7)
(7)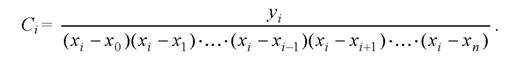 .
. 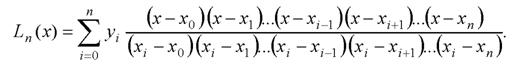 (9)
(9)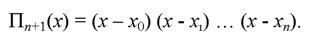 (10)
(10)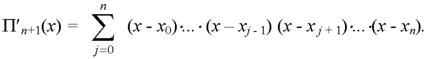
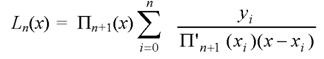
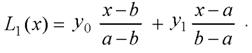
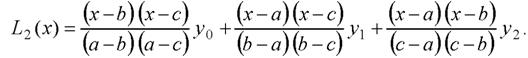
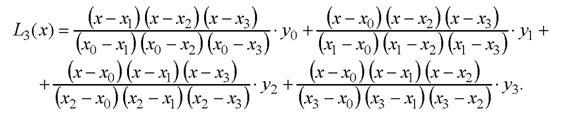
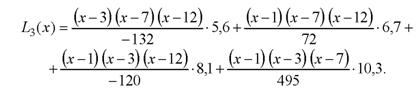
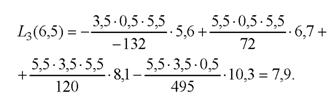
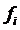
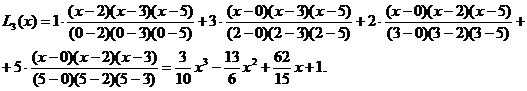
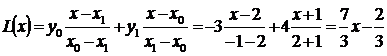 .
.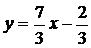 .
.