
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Принципи РІШЕННЯ СИСТЕМ НАДЛИШКОВИХ РІВНЯНЬ
Часто в ході ідентифікаційного експерименту безпосередній вимір або обчислення шуканих величин Найпростішим випадком, до якого зводяться багато інших, є такий, коли в процесі виміру одержуємо результати виду: тобто для визначення У багатьох випадках (але не завжди, що доведено в теорії ймовірностей і перевірено практикою), гіпотеза про достатню близькість значення величини (2) до точного значення вимірюваної величини вірна. Система (1), у якій число рівнянь більше числа невідомих, називається надлишкової. Вона суперечлива, несумісна. Це означає, що не можна знайти такі значення невідомих, які точно задовольняють всім рівнянням системи. Варто мати на увазі, що коефіцієнти рівнянь, і насамперед вільні члени, звичайно неточні, і тому навіть точне рішення системи (1), навіть якби воно й існувало, не давало б точних значень величин, що цікавлять нас. Можна вибрати з (1) частину рівнянь (т рівнянь), вирішити їх точно, але тоді, майже напевно, підстановка знайдених рішень у частину, що залишилася 
має найменше значення (мінімум). Принцип Лежандра називається принципом найменших квадратів, а рішення системи (1) на підставі цього принципу називається рішенням за способом найменших квадратів. Природно, виникає питання обґрунтування принципу найменших квадратів. Теоретично доведено й практично перевірено, що в більшості випадків принципу найменших квадратів можна (й потрібно) слідувати. Однак уважати його універсально придатним не можна. Питання обґрунтування принципу найменших квадратів, власне кажучи, ставиться до теорії ймовірностей. Тут розглянемо тільки геометричний зміст принципу найменших квадратів. Нехай дана система рівнянь із трьома невідомими: Крім того, припустимо, що виконано умови Як відомо, кожне лінійне рівняння (3) є рівнянням площини. В аналітичній геометрії досить просто доводиться, що числа при умовах (4) дорівнюють відстаням точки з декартовими координатами
Тепер доведемо основне твердження для
 надлишкової системи рівнянь надлишкової системи рівнянь
було найкращим у змісті принципу найменших квадратів, необхідно й достатньо, щоб
Система (6) називається нормальною системою рівнянь, що відповідає надлишковій системі (5). Треба довести, що величина приймає найменше значення при тих і тільки тих Розглянемо функцію аргументу
Ця функція, відповідно до рівності (7), повинна мати мінімум при
тобто це квадратний тричлен відносно
а це перше з рівнянь (6). Друге із цих рівнянь одержимо, розглянувши
Аналогічно знаходимо й третє з рівнянь (6). Довівши теорему, помітимо, що нормальну систему (6) можна скласти по надлишковій системі (5) у такий спосіб: множачи рівняння (5) відповідно на коефіцієнти при х і складаючи, одержуємо перше рівняння нормальної системи (6); множачи на коефіцієнти при y і складаючи, одержуємо друге рівняння системи (6) і т.д. Приклад Вирішити систему рівнянь задану нижче. Це надлишкова система (невідомих – 2, рівнянь 3), тобто типова система, яка отримується за результатами експериментів.
Множачи рівняння, відповідно, один раз на 2, 1, 3, а другий - на 1, -2, 2 і складаючи результати, одержуємо нормальну систему
рішенням якої є Приклад Вирішити систему рівнянь
Це нормальна система
має рішення Виходить, дана система сумісна, а це означає, що одне з рівнянь є наслідком інших (якщо помножити перше рівняння на Приклад Вирішити систему
Тут третє рівняння явно суперечить другому, але цілком може бути, що, вимірюючи величину
має рішення
2,5 це середнє арифметичне чисел 2 й 3.
У загальному виді, якщо перейти від системи рівнянь
до нормальної системи, одержимо
Рішення цієї системи
є точним рішенням системи рівнянь
Приклад Розглянемо приклад рішення надлишкової системи рівнянь
Множачи рівняння, відповідно, один раз на 2, 1, 3, а другий – на 1, -2, 2 і складаючи результати, одержуємо нормальну систему
Таким чином, одержуємо нормальну систему із двох рівнянь, з якої визначаємо w та І:
Отримані результати можна узагальнити для будь-яких експериментальних даних. Вирази для рішення систем надлишкових рівнянь використаються для рішення практичних завдань обробки експериментальних даних та ідентифікації параметрів, наприклад, при побудові статичних характеристик малообертових дизелів, статичних характеристик електроприводів тощо - на основі експериментальних досліджень. Слід зазначити, що існує великий клас об'єктів експериментального дослідження і ідентифікації параметрів, для яких необхідний опис змінними не першого, а більше високого ступеня. Методи рішення надлишкових систем рівнянь не першого ступеня, розглянуті, наприклад, у книзі Дринфельд Г. И., «Интерполирование и способ наименьших квадратов». -К.: ВШ, 1984.
До завдання 2
|
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 241. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
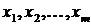 важкий, або навіть неможливий, а безпосередньо для виміру виявляються тільки деякі вирази (функції), що містять ці величини
важкий, або навіть неможливий, а безпосередньо для виміру виявляються тільки деякі вирази (функції), що містять ці величини 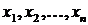 .
.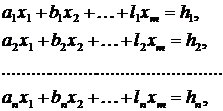 (1)
(1) 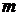 невідомих
невідомих 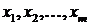 маємо систему з
маємо систему з 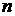 лінійних рівнянь. Число рівнянь може бути більше числа невідомих, тому що експериментатор, навіть вимірюючи одну величину, не зможе обмежитися лише одним виміром. Причина в тім, що окремі виміри неминуче містять випадкові помилки й, лише на підставі деякої сукупності вимірів, експериментатор зможе зробити більш-менш обґрунтовані висновки. Наприклад, якщо вимірюючи деяку величину п разів, експериментатор одержить у результаті величини
лінійних рівнянь. Число рівнянь може бути більше числа невідомих, тому що експериментатор, навіть вимірюючи одну величину, не зможе обмежитися лише одним виміром. Причина в тім, що окремі виміри неминуче містять випадкові помилки й, лише на підставі деякої сукупності вимірів, експериментатор зможе зробити більш-менш обґрунтовані висновки. Наприклад, якщо вимірюючи деяку величину п разів, експериментатор одержить у результаті величини 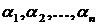 то покладається, що досить близьким до точного значення величини є середнє арифметичне:
то покладається, що досить близьким до точного значення величини є середнє арифметичне: 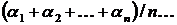 (2)
(2)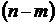 рівнянь приведе до зовсім безглуздого результату. Які наближені значення
рівнянь приведе до зовсім безглуздого результату. Які наближені значення 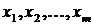 варто вважати найкращими? Очевидно такі, щоб одночасно, рівноцінної більш-менш точно, задовольнялися всі рівняння системи (1). Ще на початку XIX в. Лежандр запропонував наступний принцип: “З усіх можливих значень невідомих
варто вважати найкращими? Очевидно такі, щоб одночасно, рівноцінної більш-менш точно, задовольнялися всі рівняння системи (1). Ще на початку XIX в. Лежандр запропонував наступний принцип: “З усіх можливих значень невідомих 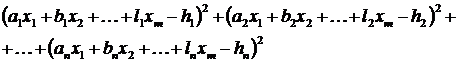

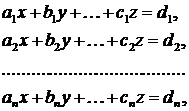 (3)
(3)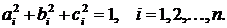 (4)
(4) 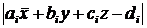
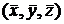 від площин (3). Отже, відшукати значення із системи (1) при умовах (4) за способом найменших квадратів означає знайти точку, для якої мінімальна середня квадратична відстань її від заданих площин (3).
від площин (3). Отже, відшукати значення із системи (1) при умовах (4) за способом найменших квадратів означає знайти точку, для якої мінімальна середня квадратична відстань її від заданих площин (3).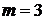 (для
(для 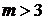 міркування аналогічні).
міркування аналогічні).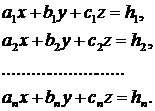
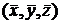 було рішенням системи трьох рівнянь
було рішенням системи трьох рівнянь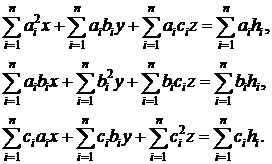 (6)
(6)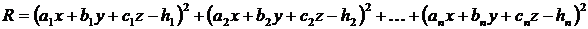
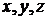 , які утворюють рішення нормальної системи (6). Легко зрозуміти, що найбільшого значення
, які утворюють рішення нормальної системи (6). Легко зрозуміти, що найбільшого значення 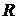 мати не може, тому що ця величина нескінченно зростає, наприклад, при
мати не може, тому що ця величина нескінченно зростає, наприклад, при 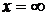 . Існування мінімуму
. Існування мінімуму 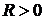 . Потрібно тільки знайти ті значення
. Потрібно тільки знайти ті значення 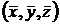 аргументів, при яких
аргументів, при яких 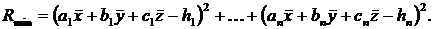 (7)
(7)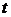 :
: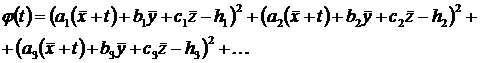
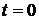 . Однак легко підрахувати, що
. Однак легко підрахувати, що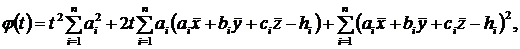
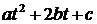 при
при 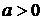 , має мінімум при
, має мінімум при 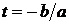 . У цьому випадку квадратний тричлен має мінімум при t = 0. Значить,
. У цьому випадку квадратний тричлен має мінімум при t = 0. Значить,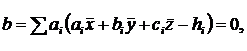
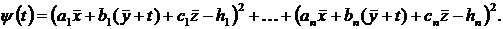
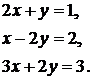
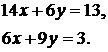
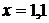 ;
; 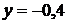 .
.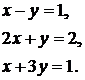
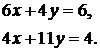
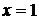 ,
, 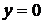 , що є точним рішенням вихідної системи.
, що є точним рішенням вихідної системи.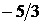 , друге на
, друге на 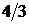 і скласти результати, то вийде третє рівняння).
і скласти результати, то вийде третє рівняння).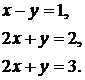
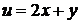 , отримано два різко відмінних результати, але немає підстав зволіти один результат іншому. Нормальна система
, отримано два різко відмінних результати, але немає підстав зволіти один результат іншому. Нормальна система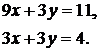
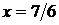 ,
, 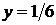 . Підстановка в задану систему показує, що рішення є точним для системи рівнянь
. Підстановка в задану систему показує, що рішення є точним для системи рівнянь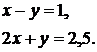
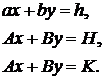
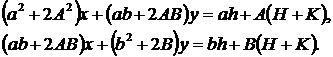
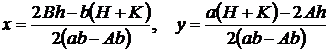
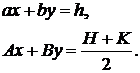
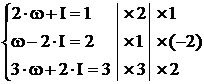
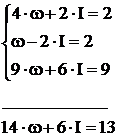 ,
, 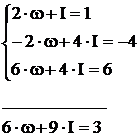 .
.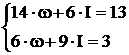 ,
,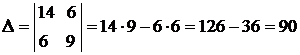 ,
,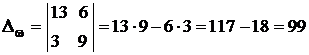 ,
,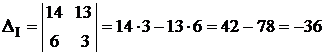 .
.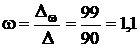 рад/с;
рад/с; 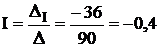 А.
А.