Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Загальна дисперсія ,міжгрупова та внутрішнлогрупова дисперсіяВідповідно до моделі однофакторного дисперсійного аналізу необхідно визначити дві дисперсії, а саме: міжгрупову (дисперсію групових середніх), зумовлену впливом досліджуваного фактора на ознаку Х, і внутрішньогрупову, зумовлену впливом інших випадкових факторів. Загальна дисперсія розглядається як сума квадратів відхилень:
оді поділ загальної дисперсії на компоненти здійснюється так:
оскільки
Таким чином, дістаємо:
Для того щоб мати виправлені дисперсії, необхідно кожну зі здобутих сум поділити на число ступенів свободи. Так, для загальної дисперсії Виправлена дисперсія де
Виправлена дисперсія
де  62) Загальний метод перевірки впливу фактора на ознаку способом порівняння дисперсій. Завдання виявлення впливу фактора на наслідки експерименту полягає в порівнянні виправлених дисперсій Порівняння двох дисперсій ґрунтується на перевірці правильності нульової гіпотези: За статистичний критерій вибирається випадкова величина що має розподіл Фішера—Снедекора з За значеннями a, Спостережуване значення критерію обчислюється за формулою Якщо Результати спостережень та обчислення статистичних оцінок зручно подати в упорядкованому вигляді за допомогою табл. 2. 63) Двофакторний дисперсійний аналіз. Нехай необхідно визначити вплив двох факторів А і В на певну ознаку Х. Для цього необхідно, щоб дослід здійснювався при фіксованих рівнях факторів А і В, а також їх одночасній дії на ознаку. При цьому дослід здійснюватимемо n раз для кожного з рівнів факторів А і В. Позначимо через Результат експерименту зручно подати у вигляді таблиці, яка поділена на блоки, в кожному з яких ураховується на певних рівнях факторів А і В їх вплив на конкретні значення ознаки |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 505. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
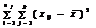 .
.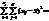
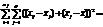
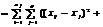
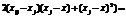
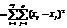
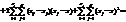
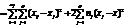
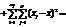
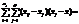
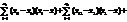
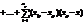
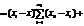
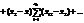
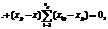
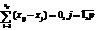
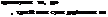
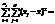
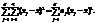
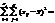
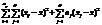
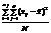 виправлена дисперсія дорівнюватиме
виправлена дисперсія дорівнюватиме 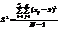 .
. 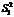 , що характеризує розсіювання всередині групи, зумовлене впливом випадкових факторів, обчислюється за формулою:
, що характеризує розсіювання всередині групи, зумовлене впливом випадкових факторів, обчислюється за формулою: 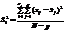 ,
, 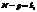 є числом ступенів свободи для
є числом ступенів свободи для 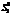 , оскільки при цьому використовується р співвідношень при обчисленні групових середніх
, оскільки при цьому використовується р співвідношень при обчисленні групових середніх 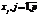 .ї
.ї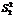 , що характеризує розсіювання групових середніх
, що характеризує розсіювання групових середніх 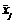 відносно загальної середньої
відносно загальної середньої 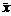 , яке викликане впливом фактора на результат експерименту ознаки Х, обчислюється за формулою:
, яке викликане впливом фактора на результат експерименту ознаки Х, обчислюється за формулою: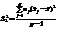 ,
, 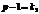 — це число ступенів свободи для
— це число ступенів свободи для 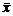 .
.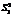 ,
, 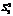 . І справді, якщо досліджуваний фактор не впливає на значення ознаки Х, то в цьому разі
. І справді, якщо досліджуваний фактор не впливає на значення ознаки Х, то в цьому разі 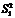 i
i 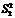 істотне, то в цьому разі вибірки слід вважати здійсненими з різних сукупностей, тобто з сукупностей з різним рівнем впливу фактора.
істотне, то в цьому разі вибірки слід вважати здійсненими з різних сукупностей, тобто з сукупностей з різним рівнем впливу фактора.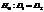 — про рівність дисперсій двох вибірок.
— про рівність дисперсій двох вибірок.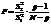 ,
, 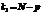 ,
, 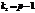 ступенями свободи.
ступенями свободи.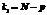 ,
, 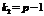 , знаходимо критичну точку (додаток 7).
, знаходимо критичну точку (додаток 7).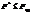 , то нульова гіпотеза про вплив фактора на результати досліджень відхиляється, а коли
, то нульова гіпотеза про вплив фактора на результати досліджень відхиляється, а коли 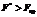 , то цим самим підтверджується вплив фактора на ознаку Х.
, то цим самим підтверджується вплив фактора на ознаку Х.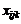 конкретне значення ознаки Х, якого вона набуває при i-му експерименті, j-му рівні фактора A і k-му рівні фактора В.
конкретне значення ознаки Х, якого вона набуває при i-му експерименті, j-му рівні фактора A і k-му рівні фактора В.