Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Моментом силы относительно оси называется проекция на ось вектора момента силы, вычисленного относительно любой точки этой оси.⇐ ПредыдущаяСтр 12 из 12
Получим удобный для практических целей способ вычисления момента силы относительно оси. Рассмотрим силу
Умножая слева векторно на вектор
Записывая последнее равенство в проекции на ось
так как вектор Таким образом,
Модуль момента силы относительно оси равен произведению модуля проекции силы на плоскость, перпендикулярную оси, на кратчайшее расстояние от оси до этой проекции. Момент силы относительно оси больше нуля, если с положительного конца оси поворот тела вокруг оси под действием силы виден против хода часовой стрелки и отрицателен в противоположном случае.
Заметим, что момент силы относительно оси равен нулю, если линия действия силы параллельна оси или пересекает ось. Другими словами, момент силы относительно оси равен нулю, если ось и линия действия силы лежат в одной плоскости (компланарны).
Пример 4.1.
На горизонтальном валу 
Рассмотрим равновесие вала
Первые три из уравнений равновесия принимают вид:
При составлении уравнений моментов удобно использовать вспомогательные чертежи. Например, составляя уравнение моментов относительно оси
Составим уравнение моментов относительно оси
Уравнение моментов относительно оси
Полученная система уравнений позволяет определить все искомые силы по заданным размерам конструкции.
Заметим, что составлять вспомогательные чертежи не обязательно, но удобно, особенно при отсутствии соответствующих навыков. Другой приём, полезный при вычислении момента силы относительно оси, состоит в том, что сила раскладывается на составляющие, моменты которых достаточно просто вычисляются.
Пример 4.2
Однородная прямоугольная пластина весом
Рассмотрим равновесие пластины. Силовая расчётная схема представлена на Рис. 4.7. Сила реакции троса
Заметим, что линия действия силы
Угол
Условия равновесия имеют вид:
Полученная система уравнений позволяет определить все неизвестные величины.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 8.13; 8.14; 8.15; 8.16; 8.18; 8.19; 8.21; 8.22; 8.23; 8.24; 8.25; 8.26.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-4
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ:
ЛИТЕРАТУРА:
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 708. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
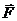 , произвольным образом расположенную по отношению к оси
, произвольным образом расположенную по отношению к оси 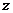 . Проведём через точку приложения силы плоскость, перпендикулярную оси (Рис. 4.1). Пусть
. Проведём через точку приложения силы плоскость, перпендикулярную оси (Рис. 4.1). Пусть 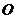 – точка пересечения этой плоскости с осью. Разложим силу
– точка пересечения этой плоскости с осью. Разложим силу  перпендикулярна оси, а вторая
перпендикулярна оси, а вторая  параллельна оси:
параллельна оси: .
.
 , получаем:
, получаем: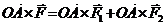 .
. ,
, перпендикулярен оси и не даёт на неё проекции.
перпендикулярен оси и не даёт на неё проекции. жёстко закреплены два шкива, плоскости которых перпендикулярны валу. В точках
жёстко закреплены два шкива, плоскости которых перпендикулярны валу. В точках  и
и  установлены цилиндрические шарниры. Намотанные на шкивы тросы переброшены через блоки
установлены цилиндрические шарниры. Намотанные на шкивы тросы переброшены через блоки  и
и  и растягиваются грузами
и растягиваются грузами  и
и  (Рис. 4.2). Определить вес
(Рис. 4.2). Определить вес  груза
груза  . Определить также реакции шарниров. Трением пренебречь.
. Определить также реакции шарниров. Трением пренебречь.
 ;
;  .
.



 , изобразим вид с положительного конца оси
, изобразим вид с положительного конца оси  (Рис. 4.4). В этом случае уравнение моментов относительно оси
(Рис. 4.4). В этом случае уравнение моментов относительно оси 

 (Рис. 4.5а). Заметим, что на таком чертеже сила
(Рис. 4.5а). Заметим, что на таком чертеже сила  не видна, а сила
не видна, а сила  видна частично – только её составляющая по оси
видна частично – только её составляющая по оси  ).
).


 и троса
и троса  (Рис. 4.6). На пластину действуют сила
(Рис. 4.6). На пластину действуют сила  и пара сил с моментом
и пара сил с моментом 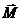 . Даны размеры пластины и угол
. Даны размеры пластины и угол  . Определить реакции опор.
. Определить реакции опор. разложена на две составляющие:
разложена на две составляющие:  ; (
; (  ), линия действия которой проходит через начало координат, и
), линия действия которой проходит через начало координат, и  ; (
; (  ), линия действия которой параллельна оси
), линия действия которой параллельна оси 


 (точнее значения тригонометрических функций этого угла) легко вычислить через заданные длины сторон пластины (Рис. 4.8):
(точнее значения тригонометрических функций этого угла) легко вычислить через заданные длины сторон пластины (Рис. 4.8):