Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приведение системы сил к одному центру
Одной из основных задач статики является приведение системы сил к простейшему виду, т.е. преобразование заданной системы сил в другую, ей эквивалентную, но содержащую минимальное число сил. Одним из способов решения такой задачи является приведение системы сил к одному центру (метод Пуансо).
Теорема. Произвольная система сил эквивалентна системе, состоящей из одной силы, равной геометрической сумме всех сил системы, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен сумме моментов всех сил системы относительно этой точки.
Доказательство. Пусть задана система сил Проделывая такую операцию с каждой силой системы, заменяем заданную систему сил эквивалентной, которая состоит из приложенных в точке В соответствии с аксиомой 1 система сил
В соответствии с теоремой о сложении пар система пар сил 
Таким образом, установлены две важнейшие характеристики системы сил:
главным вектором системы сил называется геометрическая сумма всех сил системы:
главным моментом системы сил относительно некоторого центра O называется геометрическая сумма моментов всех сил системы относительно точки O:
Вектор главного момента изображают приложенным в той точке Заметим, что главный вектор и главный момент системы сил представляют собой чисто геометрические величины и не могут рассматриваться как некоторая сила или момент некоторой силы. Доказанную выше теорему о приведении системы сил к одному центру теперь можно сформулировать в виде:
Произвольная система сил эквивалентна системе, состоящей из одной силы, равной главному вектору системы сил, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен главному моменту системы сил относительно этой точки.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
ЛЕКЦИЯ 3 |
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 878. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 , произвольным образом расположенных в пространстве (Рис. 2.1). Выберем любую точку
, произвольным образом расположенных в пространстве (Рис. 2.1). Выберем любую точку 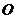 в качестве центра приведения. Рассмотрим любую силу системы
в качестве центра приведения. Рассмотрим любую силу системы  . На основании аксиомы 2 приложим к точке
. На основании аксиомы 2 приложим к точке  , причём,
, причём,  . Таким образом, сила
. Таким образом, сила  , приложенной в точке
, приложенной в точке  , момент которой равен моменту силы
, момент которой равен моменту силы 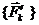 и пар сил
и пар сил  , плоскости действия которых имеют общую точку
, плоскости действия которых имеют общую точку  , приложенной в точке
, приложенной в точке 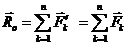 .
. .
.