Парой сил называется система двух сил, равных по модулю и            действующих по параллельным прямым в противоположные стороны.

Плоскость, в которой расположены силы пары, называется плоскостью действия пары сил. Кратчайшее расстояние между линиями действия сил пары называется плечом пары сил.

Рис. 1.7		Рис. 1.8

Очевидно, такую силовую систему нельзя заменить одной силой, поскольку геометрическая сумма сил, образующих пару, равна нулю. В тоже время опыт показывает, что под действием пары сил тело не может оставаться в покое. Возникает вопрос о характеристике такой силовой системы.

Сейчас мы остановимся только на некоторых свойствах пары сил. В дальнейшем, после изучения основных теорем статики, мы вернёмся к рассмотрению этой силовой системы.

Вычислим сумму моментов сил, образующих пару, относительно произвольно выбранной точки  (Рис. 1.7):

  Учитывая, что   и   получаем:

Как видно, сумма моментов сил, образующих пару сил, не зависит от точки, относительно которой эта сумма вычисляется, и может быть принята за характеристику пары сил.

Моментом пары сил называется сумма моментов сил, образующих пару,

              вычисленная относительно произвольно  выбранной точки.

Момент пары сил можно вычислить как момент одной из сил пары относительно точки приложения другой силы той же пары, поскольку эта вторая сила не создаёт момент относительно своей точки приложения:

Момент пары сил – вектор свободный; он располагается перпендикулярно плоскости действия пары сил, причём направлен в ту сторону, откуда возможный поворот тела под действием пары виден против хода часовой стрелки (Рис. 1.8). Модуль момента пары равен произведению модуля одной из сил пары на её плечо:

Сложение пар сил, расположенных в пересекающихся плоскостях

Теорема

Две пары сил, плоскости действия которых имеют хотя бы одну               общую точку, эквивалентны одной паре сил, момент которой               равен сумме моментов слагаемых пар.

Доказательство.  Если две плоскости имеют общую точку O, то они или пересекаются, или совпадают. Рассмотрим более общий случай пересекающихся плоскостей. Пусть   –  плоскость действия пары сил ;   – плоскость действия пары сил ;   –  точки приложения сил. Выберем на линии пересечения плоскостей любую точку C (если плоскости действия пар сил совпадают, то C любая точка плоскости). Разложим каждую из четырёх заданных сил на составляющие  и , линии действия которых проходят через точки O и C соответственно. Перенося составляющие вдоль их линий действия в точки O и C соответственно, заменим приложенные в точках O и C силы  и  равнодействующими   и  (Рис. 1.9).

Силы  и  образуют пару сил, поскольку

      так как    

Рис. 1.9

Момент пары сил  равен сумме моментов слагаемых пар:

так как

       Подводя итог, заметим, что на основании результатов, полученных в этой главе, можно

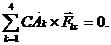
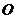1. любую систему сходящихся в некоторой точке  сил заменить равнодействующей , приложенной в точке  и равной геометрической сумме всех сил системы;

1. систему пар сил, плоскости действия которых имеют хотя бы одну общую точку, можно заменить одной парой сил, момент которой равен сумме моментов всех пар системы.

ОСНОВНЫЕ ТЕОРЕМЫ СТАТИКИ