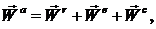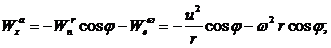Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление абсолютной скорости и абсолютного ускорения точки⇐ ПредыдущаяСтр 13 из 13 Напомним теорему сложения скоростей при сложном движении точки:
абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей: Теорема сложения ускорений при сложном движении точки имеет вид: где вектор называется ускорением Кориолиса. Таким образом,
абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений. Пример 3.3 Круглая трубка радиуса
Относительное движение шарика представляет собой движение по окружности радиуса
Вычислим относительную скорость и относительное ускорение шарика:
Трубка сообщает шарику переносную скорость  и переносное ускорение Угол между осью вращения трубки, вдоль которой направлен вектор ее угловой скорости, и вектором относительной скорости шарика равен
Для определения направления ускорения Кориолиса удобнее всего воспользоваться правилом Жуковского. Абсолютная траектория шарика в данном случае очевидна – это все та же окружность с центром
Используя теорему Кориолиса (3.12), получаем:
Направления векторов указаны на Рис. 3.5. Ускорение Кориолиса и относительная скорость представлены на рисунке для случая
Пример 3.4 Лопатка
Точка
Направление ускорения Кориолиса определяем по правилу Жуковского. Модуль ускорения Кориолиса равен
Используя теорему Кориолиса, найдем проекции абсолютного ускорения частицы
Остается определить Отсюда Таким образом, Окончательно получаем:
Пример 3.5 Диск радиуса
Рассмотрим переносное движение – его совершает диск. Точка
направлена по касательной к этой окружности в сторону вращения диска, т.е. перпендикулярно плоскости диска в отрицательном направлении координатной оси
Вектор ускорения Кориолиса точки
При перемещении точки Таким образом,
Используя теорему сложения скоростей
находим проекции вектора абсолютной скорости на оси подвижной системы координат:
Используя теорему Кориолиса
находим проекции абсолютного ускорения точки на оси подвижной системы координат:
Примечание. Последняя задача позволяет проиллюстрировать некоторые явления, связанные с вращением Земли, в частности, размыв берегов рек. Как видно, вращение Земли приводит к возникновению у частиц воды кориолисова ускорения, направленного перпендикулярно линии берегов. Наличие такого ускорения приводит к тому, что в северном полушарии дополнительно подмывается правый берег, который на прямолинейных участках рек заметно выше левого берега. В южном полушарии более высокий левый берег. Это явление в географии отражено в законе Бэра. ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ: Из сборника задач И.В.Мещерского: 22.10; 22.14; 22.17; 22.26; 23.1; 23.9; 23.13; 23.18; 23.19; 23.27; 23.29; 23.34; 23.47; 23.48; 23.49; 23.56.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-23; СР-24; СР-25. КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ:
ЛИТЕРАТУРА:
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 270. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||

 ,
, 
 вращается вокруг горизонтальной оси
вращается вокруг горизонтальной оси  по часовой стрелке с постоянной угловой скоростью
по часовой стрелке с постоянной угловой скоростью  . Внутри трубки около ее точки
. Внутри трубки около ее точки  колеблется шарик
колеблется шарик  , причем так, что
, причем так, что  (Рис. 3.5). Определить скорость, касательное и нормальное ускорения в абсолютном движении шарика в любой момент времени.
(Рис. 3.5). Определить скорость, касательное и нормальное ускорения в абсолютном движении шарика в любой момент времени.
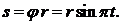


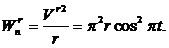


 , так что
, так что




 рабочего колеса турбины, вращающегося против хода часовой стрелки замедленно с угловым ускорением
рабочего колеса турбины, вращающегося против хода часовой стрелки замедленно с угловым ускорением 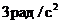 , имеет радиус кривизны 0.2 м и центр кривизны в точке
, имеет радиус кривизны 0.2 м и центр кривизны в точке  , причем
, причем  м. Частица воды
м. Частица воды  по отношению к лопатке. Определить абсолютное ускорение частицы
по отношению к лопатке. Определить абсолютное ускорение частицы 
 . Определим переносное ускорение точки:
. Определим переносное ускорение точки:


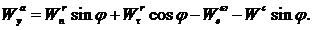


 и
и  . Для этого используем теорему косинусов (Рис. 3.7):
. Для этого используем теорему косинусов (Рис. 3.7):

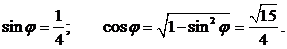

 с постоянной угловой скоростью
с постоянной угловой скоростью  . Определить абсолютную скорость и абсолютное ускорение точки
. Определить абсолютную скорость и абсолютное ускорение точки 
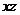 . Переносная скорость
. Переносная скорость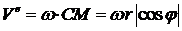
 . Поскольку вращение диска по условию равномерное, отличным от нуля оказывается только осестремительное ускорение:
. Поскольку вращение диска по условию равномерное, отличным от нуля оказывается только осестремительное ускорение:
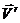 и
и  , причем, в ту сторону, откуда кратчайшее совмещение направления вектора
, причем, в ту сторону, откуда кратчайшее совмещение направления вектора  .
.
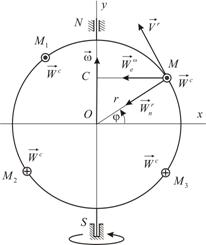
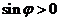 , т.е. пока
, т.е. пока  (точка
(точка  ). При пересечении точкой
). При пересечении точкой  ускорение Кориолиса обращается в нуль. При движении точки в нижней части диска, т.е. при
ускорение Кориолиса обращается в нуль. При движении точки в нижней части диска, т.е. при  , проекция ускорения Кориолиса на направление оси
, проекция ускорения Кориолиса на направление оси  направлен от нас (точки
направлен от нас (точки  и
и  ).
).