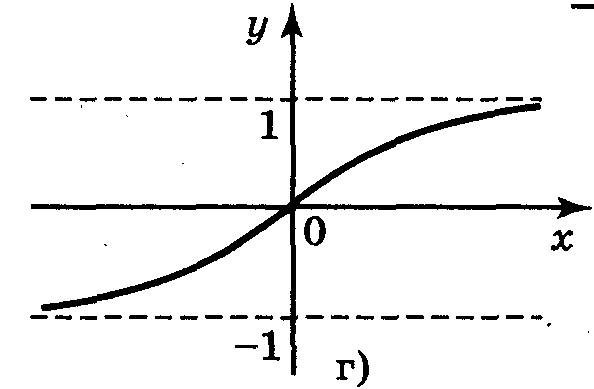Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Самостійне вивчення з розробкою конспекту та розв’язуванням задач.План. 1. Історія виникнення поняття функції. 2. Поняття функціональної залежності. 3. Числова функція. Область визначення функції. 4. Способи задання функції Форми поточного та підсумкового контролю самостійної роботи: 1. Поточний: · перевірка конспектів · усне опитування · розв’язування задач. 2. Підсумковий: · тематична контрольна робота · державна підсумкова атестація
Історія виникнення поняття функції.
Поняття функції виникло в математиці порівняно недавно. Для того щоб збагнути доцільність його введення й одержати перші доволі чіткі означення, знадобилися зусилля видатних математиків багатьох поколінь. Революційні зміни в математиці, що відбулися в ХVІІ столітті, готували своїми працями вчені різних країн і народів. Але передусім варто назвати імена П. Ферма (1601—1665), Р. Декарта (1596—1650), І. Ньютона (1643—1727), Г. В. Лейбніца (1646—1716). Необхідні передумови для формування поняття функції було створено в 30-х роках ХVII століття, коли виникла аналітична геометрія, яка на відміну від класичної геометрії Стародавньої Греції активно залучала алгебру до розв’язування геометричних задач. Практично одночасно (і незалежно один від одного) французькі математики П. Ферма і Р. Декарт помітили, що завдяки введенню системи координат на площині і заданню фігур їхніми рівняннями можна розв’язання багато задач геометрії звести до дослідження рівнянь геометричних фігур. На честь Декарта, який дав розгорнутий виклад нового методу в книгах «Геометрія» і «Міркування про метод», прямокутну систему координат пізніше було названо декартовою. Зауважимо, що одночасно формувалася й алгебра, створювалося саме те «буквене числення», за допомогою якого нині перетворюють алгебраїчні вирази, розв’язують рівняння, текстові задачі і т. ін.  Великий англійський математик і фізик І. Ньютон, досліджуючи залежності координат точки, що рухається, від часу, фактично вже досліджував функції. Хоча не Ньютон увів це поняття, він чітко усвідомлював його значення. Так, у 1676 році вчений зазначав: «Я не міг би, вочевидь, здобути ці загальні результати, аби не відвернувся від розгляду фігур і не звів усе просто до дослідження ординат» (тобто фактично функцій від часу). Сам термін «функція» вперше вжив великий німецький математик і філософ Г. В. Лейбніц — спочатку в рукопису (1673), а потім і в друкованому вигляді (1692). Латинське слово function перекладається як «здійснення», «виконання» (дієслово fungor означає «виражати»). Лейбніц увів поняття функції, щоб схарактеризувати різні параметри, позв’язані з положенням точки на площині. Згодом Лейбніц і його учень Й. Бернуллі (1667—1748) прийшли до розуміння функції як аналітичного виразу й у 1718 році подали таке означення: «Функцією змінної величини називається кількість, складена в який завгодно спосіб з цієї змінної та сталих». Л. Ейлер у своїй книзі «Вступ до аналізу» (1748) сформулював означення функції так: «Функція змінної кількості — це аналітичний вираз, складений у деякий спосіб із цієї змінної кількості та чисел або сталих кількостей». Ейлер упровадив і застосовувані нині позначення для Сучасне означення числової функції, в якому це поняття вже не пов’язувалося способом задання, дали незалежно один від одного російський математик М. І. Лобачевський (1834) і німецький математик Л. Діріхле (1837). Основна ідея такого означення полягала ось у чому: не істотно, в який спосіб (це може бути будь-яке правило, не лише аналітичний вираз) кожному х поставлено у відповідність певне значення у, важливо тільки, що цю відповідність установлено. Сучасне поняття функції з довільними областями визначення і значень сформувалося, власне кажучи, зовсім недавно, на початку ХХ століття, у працях творця теорії множин Г. Кантора (1845—1918). Складний і дуже тривалий шлях розвитку поняття функції доволі типовий. Для того щоб усвідомити необхідність уведення нового абстрактного поняття, потрібно виокремити його в процесі розв’язування багатьох конкретних задач і дати означення, що якнайчастіше відбиває його зміст. До поняття функції математики йшли, відштовхуючись від конкретних задач математики та її застосування. Це відбувалося в процесі створення нового могутнього апарата досліджень — інтегрального і диференціального числення. Відкриття інтегрального і диференціального числення, центральним поняттям якого Ейлер назвав функцію («Увесь аналіз нескінченного обертається навколо змінних кількостей і їхніх функцій»), розширило можливості математики. 2. Поняття функціональної залежності. Процеси реального світу тісно пов'язані між. собою. Серед різноманіття явищ вчені виділили такі, у яких взаємозв'язок величин настільки тісний, що, знаючи значення однієї з них, можна визначити значення другої величини. Наприклад, знаючи сторону квадрата, можна знайти його площу або периметр. Залежність змінної у від змінної х, при якій кожному значенню χ відповідає єдине значення у, називається функцією. З поняттям функції ви познайомилися в курсі алгебри неповної школи. Поняття функції є важливим поняттям курсу алгебри і початків аналізу, отже, ми повинні згадати і узагальнити відомості про функції. Крім того, досліджуючи властивості функцій, ми маємо можливості ґрунтовніше пізнати реальний світ. Числова функція. Область визначення функції. У курсі алгебри і початків аналізу ми будемо користуватися таким означенням числової функції. Числовою функцією з областю визначення D називається залежність, при якій кожному числу x із множини D ставиться у відповідність єдине число y. Функції позначають латинськими (інколи грецькими) буквами. Розглянемо довільну функцію f. Число y, яке відповідає числу x (на рисунку 1 це показано стрілкою), називають значенням функції f у точці x і позначають f (x). Область визначення функції f — це множина тих значень, яких може набувати аргумент x. Вона позначається D (f). Область значень функції f — це множина, яка складається із всіх чисел f (x), де x належить області визначення. Її позначають E (f). Способи задання функції Функцію можна задати за допомогою таблиці, графіка, формули. Найчастіше функцію задають за допомогою формули. При цьому якщо не дано додаткових обмежень, то областю визначення функції, заданої формулою, вважають множину всіх значень змінної, при яких ця формула має сенс. Наприклад, якщо кожному значенню х із множини дійсних чисел поставити у відповідність квадрат цього числа, то-функцію можна записати у вигляді формули: у = х2 або f(x)= x2. Функцію також можна задати за допомогою таблиці. Розглянемо приклад. Результати вимірювання температури тіла хворого в залежності від часу подано в таблиці:
Залежність у·= f(x) є функцією, х — незалежна змінна, у — залежна змінна. f(9) = 39, f(12) = 38.5,..., f(24) = 37. D(f) = {9;12;15; 18; 21; 24}. E(f) = {39; 38,5; 38,3; 37,3; 37,1; 37}. Наприклад, якщо кожному значенню х із множини дійсних чисел поставити у відповідність квадрат цього числа, то-функцію можна записати у вигляді формули: у = х2 або f(x)= x2. Областю визначення функції у = f(x), яка задана формулою, називається множина тих значень, які може приймати х, тобто формула має зміст (усі дії, вказані формулою, можна виконати). Наприклад, формула Отже, для функції При знаходженні області визначення слід пам'ятати: 2) Якщо функція є многочленом у = аn хn + αn-1 xn-1 +... + α1x + a0, то D(y) = (- 2) Якщо функція має вигляд у = 3) Якщо функція має вигляд у = Приклад. Знайдемо область визначення дробово-раціональної функції
Розв’язування. Корені многочлена
Графіком функції f називають множину всіх точок (x; y) координатної площини, де y = f(x), а x пробігає всю область визначення функції f. Підмножина координатної площини є графіком будь-якої функції, якщо вона має не більш як одну спільну точку з будь-якої прямої, паралельної осі Oy. Наприклад, множина, зображена на рис. 1, не є графіком функції, оскільки вона містить дві точки з однією і тією самою абсцисою a, але різними ординатами b1 і b2. Якби ми розглядали цю множину як графік функції, то довелося б вважати, що ця функція має при x = a відразу два значення b1 і b2, що суперечить означенню функції. Часто функцію задають графічно. При цьому для будь-якого x0
№1. Знайдіть значення функції: a) f(x) =
Відповідь: а) f(1) = 2, f(-1) = 0; f(5) = 1,2; б) f(3) = 0; f(12) = 3; f(52) = 7
а)таблиці; б)графіка. Відповідь:
б) рис. 1
№3. Знайдіть область визначення функції: а) у = х2 + х3; б) Відповідь: a) D(y) = R; б) D(y) = (- г) D(y) = (- є) D(y) = [-6; + №4. Знайдіть область значень функції: а) у = Відповідь: а) Е(у) = [2; +
№5. Для функцій, графіки яких зображено на рис.2 , вкажіть D(y) і Е(у).
Рис. 2 Відповідь: а) D(у) = [-1;1]; Е(у) = [0;1]; б) D(y) = [-1;1]; E(y) = [-2;2]; в) D(y) = (-1;1); E(у) = R; г) D(y) = R; Е(у) = (-1;1). 6. Які із ліній, зображених на рисунку 3, є графіком функції? Чому?
Відповідь: а); в). |
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 228. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Лекційний матеріал до теми.
Лекційний матеріал до теми. має сенс при всіх
має сенс при всіх  , тому областю визначення функції
, тому областю визначення функції  вважають множину всіх дійсних чисел, що не дорівнюють нулю. Область її значень збігається з областю визначення і є об’єднанням інтервалів (–∞; 0) і (0; ∞).
вважають множину всіх дійсних чисел, що не дорівнюють нулю. Область її значень збігається з областю визначення і є об’єднанням інтервалів (–∞; 0) і (0; ∞).
 ; +
; +  , де f(x) і g(x) — многочлени, то слід вважати g(x)
, де f(x) і g(x) — многочлени, то слід вважати g(x)  0 (знаменник дробу не дорівнює 0).
0 (знаменник дробу не дорівнює 0). , то слід вважати f(x) > 0 (арифметичний квадратний корінь існує тільки з невід'ємних чисел).
, то слід вважати f(x) > 0 (арифметичний квадратний корінь існує тільки з невід'ємних чисел).
 — числа 0, 1 і 2. Тому
— числа 0, 1 і 2. Тому  (0; 1)
(0; 1) 

 у точках 1; -1; 5; б) f(x) =
у точках 1; -1; 5; б) f(x) =  у точках 3; 12; 52.
у точках 3; 12; 52. №2. Функцію задано формулою у = x2 на області визначення D = {-3; -2; -1; 0; 1; 2; 3}. Задайте її за допомогою:
№2. Функцію задано формулою у = x2 на області визначення D = {-3; -2; -1; 0; 1; 2; 3}. Задайте її за допомогою: ; в)
; в) 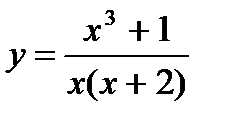 ; д)
; д)  ; є)
; є)  .
. (3; +
(3; + 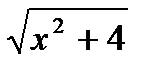 ; б) у =
; б) у =