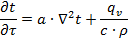Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальное уравнение теплопроводности и методы его решения.При выводе дифференциального уравнения теплопроводности считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры λ, с(теплоемкость), и ρ (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения, например, в тепловыделяющих элементах атомных реакторов, или при прохождении тока в электрических проводниках. Внутренние источники теплоты характеризуются величиной qv — количеством теплоты, которое выделяется в единице объема в единицу времени. В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQвн и внесенная извне в элементарный объем путем теплопроводности dQm за время dτ, идет на изменение внутренней энергии вещества, содержащегося в этом объеме: .
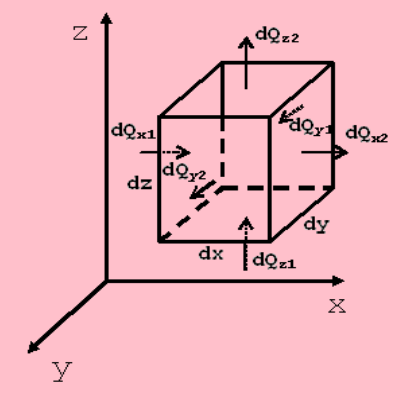
Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz. Количество теплоты, которое проходит путем теплопроводности внутрь выделенного объема в направлении оси ОX через элементарную площадку dy·dz за время dτ:
На противоположной грани параллелепипеда температура получит приращение Количество тепла, отведенного через эту грань: .
Разница количества теплоты, подведенного к элементарному параллелепипеду и отведенного от него, представляет собой теплоту, внесенную путем теплопроводности в направлении оси ОX:
Аналогично: .
Полное количество теплоты внесено в элементарный параллелепипед путем теплопроводности
 Здесь произведение dx·dy·dz представляет собой объем элементарного параллелепипеда dv. Количество теплоты, которое выделилось в элементарном объеме за счет внутренних источников: .
Приращение внутренней энергии можно выразить через массу параллелепипеда ρ·dv, теплоемкость с и приращение температуры
Подставляя выражения для dQm, dQвн и dU в уравнение (9.10), после соответствующих сокращений получаем: .
Сумма вторых частных производных любой функции в математическом анализе носит название оператора Лапласа и обозначается следующим образом: .
Величину
Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Коэффициент температуропроводности a является физическим параметром вещества. Из уравнения (9.12) следует, что изменение температуры во времени для любой точки тела пропорционально величине a. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 408. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
.
 и будет составлять
и будет составлять  .
.


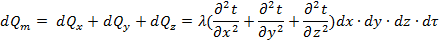

 :
:


 называют коэффициентом температуропроводности и обозначают буквой a. В указанных обозначениях уравнение (9.11) примет вид: .
называют коэффициентом температуропроводности и обозначают буквой a. В указанных обозначениях уравнение (9.11) примет вид: .