
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теплопроводность стенок различной конфигурации при стационарном режиме.Стр 1 из 36Следующая ⇒ Виды процессов тепло- и массообмена. Поля температур. Внешний и внутренний теплообмен. Температурный градиент. Виды теплообмена: Теплопроводность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела. Конвекция - процесс теплообмена между поверхностью тела и окружающей средой происходит в жидкостях или газах от поверхности твердого тела или его поверхности одновременно конвекцией и теплопроводностью. Тепловое изучение -перенос теплоты осуществляется электромагнитными волнами. Температурный градиент - величина изменения температуры на единицу длины в направлении распространения теплоты, т. е. по направлению нормали к изотермической поверхности. Выражают в Кельвинах на метр (К/м) или в градусах Цельсия на метр (°С/м). Теплообмен: Внешний– передача теплоты от окружающей среды к поверхности материала путём излучения или конвекции. Внутренний –это распространение теплоты в самом металле.
Закон Фурье. Коэффициент теплопроводности. Теплопроводность

a=λ/(PС_р ) [м^2/c] Теплопроводность стенок различной конфигурации при стационарном режиме. В случае стационарной теплопроводности t-ра в любой точке тела неизменна во времени, поэтому процессы теплопереноса описывают диф. уравнением стационарной теплопроводности. При решении задач стационарной теплопроводности должны задаваться граничные условия, т.к. начальные условия не имеют смысла. Рассмотрим теплопроводность через тонкую стенку, т.е. для пластины неограниченно простирающейся вдоль осей Y и Z, но имеющей конечную толщину S в направлении оси X. Площадь через которую проходит тепловой поток постоянна. Коэф. теплопроводности стенки Проинтегрировав это уравнение один раз получим: (9) Из полученного выражения следует, что плотность теплового потока – величина постоянная по толщине пластины, т.к. из закона Фурье: Этот результат вытекает также из з-на сохранения энергии. Т.к. для сохранения стационарного режима необходимо, чтобы кол-во теплоты, проходящее через поверхности парал. плоскостей, были равны. Поскольку в противном случае T пластины должна изменяться во времени.
Из выражения (11) следует, что распределений t-р по сечению пластины явл. линейным. Это выражение только при условии постоянства коэф-та теплопроводности Граничные условия 1ого рода В этом случае задаём Т1 и Т2 на поверхностях пластины, т.е. t(0)=t1 и t(S)=t2. Используя эти граничные условия можно записать C1=t1 Второе граничное условие даёт С1=(t2-t1)/S=-( t1- t2) /S. Т.о. распределение t-р по толщине пластины имеет вид t(x)= t1-( t1- t2)x. Плотность теплового потока с учётом з-на Фурье Граничные условия 2ого рода При этом задано значение плотности теплового потока q на поверхностях пластины, т.е. q=const. Но в этом случае единственное решение задачи теплопроводности не существует, т.к. С1= Граничные условия 3ого рода
qср 1-1= поскольку процесс стационарный все эти три потока равны между собой: q1=q2=q3=q откуда имеем K – коэф. теплопередачи
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 478. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

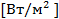 :– передача теплоты от одних частей тела к другим, обусловленная разностью температур, без заметного перемещения макрочастиц. Для газов - это передача кинетической энергии от одних молекул к другим; в металлах – электропроводность, в диалектриках – передача связанных колебаний атомов и молекул. Процесс передачи теплоты теплопроводности происходит тем интенсивнее, чем выше
:– передача теплоты от одних частей тела к другим, обусловленная разностью температур, без заметного перемещения макрочастиц. Для газов - это передача кинетической энергии от одних молекул к другим; в металлах – электропроводность, в диалектриках – передача связанных колебаний атомов и молекул. Процесс передачи теплоты теплопроводности происходит тем интенсивнее, чем выше  Это обусловлено основным законом теплопроводности – Закон Фурье.
Это обусловлено основным законом теплопроводности – Закон Фурье. 
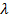 – коэфф. теплопроводности
– коэфф. теплопроводности 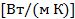
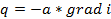
 - коэфф. температуропроводности
- коэфф. температуропроводности

 C1 – произвольная константа интегрирования
C1 – произвольная константа интегрирования
 Вторично проинтегрировав ур-е (9) получим: (11) t(x)=C1x+C2, С2 – вторая производная.
Вторично проинтегрировав ур-е (9) получим: (11) t(x)=C1x+C2, С2 – вторая производная.
 – полный тепловой поток
– полный тепловой поток . Для решения задачи в приграничных условиях 2ого рода необходимо задать дополнительное уравнение. Например: t-ру на одной из поверхностей, или t-ру среды и коэф. теплоотдачи.
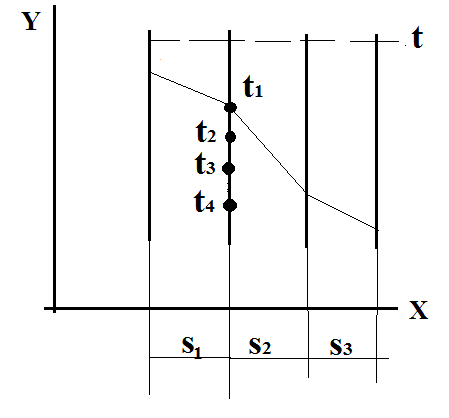
. Для решения задачи в приграничных условиях 2ого рода необходимо задать дополнительное уравнение. Например: t-ру на одной из поверхностей, или t-ру среды и коэф. теплоотдачи.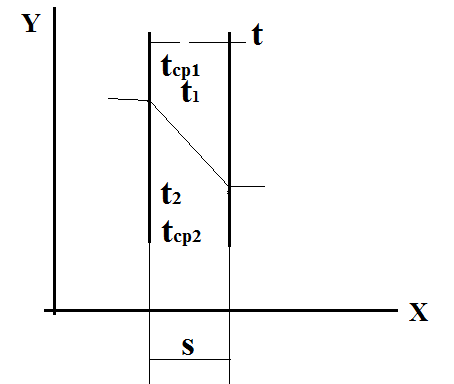 В этом случае задаётся t-ра среды и коэф. теплоотдачи слева и справа пластины(рассматривается конвективный теплообмен ). Распределение t-р по толщине пластины имеет линейный характер. В среде по обе стороны от пластины имеет место плавное изменение t-ры. Рассматриваемый процесс представляет собой процесс теплопередачи, т.е. включает коллективную теплоотдачу от среды к поверхности пластины, теплопроводностьв пластине и конвективную теплоотдачу от поверхности пластины к среде. Тепловые потоки для каждого из указанных процессов:
В этом случае задаётся t-ра среды и коэф. теплоотдачи слева и справа пластины(рассматривается конвективный теплообмен ). Распределение t-р по толщине пластины имеет линейный характер. В среде по обе стороны от пластины имеет место плавное изменение t-ры. Рассматриваемый процесс представляет собой процесс теплопередачи, т.е. включает коллективную теплоотдачу от среды к поверхности пластины, теплопроводностьв пластине и конвективную теплоотдачу от поверхности пластины к среде. Тепловые потоки для каждого из указанных процессов:

 Тогда q=K
Тогда q=K  Суммарное тепловое сопротивление
Суммарное тепловое сопротивление 
 – внутреннее сопротивление стенки,
– внутреннее сопротивление стенки,  – внешнее сопротивление.
– внешнее сопротивление.