
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Краевые задачи при определении потенциалаСтр 1 из 6Следующая ⇒ ГЛАВА 2. ТЕОРИЯ ПОЛЯ СИЛЫ ТЯЖЕСТИ Общие сведения Поле силы тяжести для любого небесного тела состоит из силы притяжения, обусловленной законом всемирного притяжения Ньютона, и центробежной силой, обусловленной вращением планеты. Имеются и некоторые другие силы, влияющие на силу тяжести, но о них пойдет речь несколько позже. Заметим, что центробежная сила легко и довольно точно определяется по известной угловой скорости и расстоянию от оси вращения тела для любой точки небесного тела. Поэтому основное внимание обычно уделяют потенциалу силы притяжения или гравитационному потенциалу. Под теорией потенциала понимают методы определения скалярной функции Основное свойство потенциала заключается в том, что производные от этой функции пропорциональны проекциям силы, а последняя, согласно второму закону Ньютона пропорциональна ускорению т.е. Следовательно, производные от потенциала пропорциональны ускорениям, а не скоростям как у обычной функции. Под теорией потенциала понимают теорию отыскания потенциала U и его градиента, то есть ÑU. Исходными уравнениями для отыскания этих функций являются однородные линейные дифференциальные уравнения второго порядка в частных производных, которые получают как дивергенцию от градиента потенциала U ,то есть оператор Лапласа. Лапласом было получено уравнение потенциала объемных масс во внешнем пространстве, а именно, им доказано что Таким образом, лапласиан во внешнем пространстве равен нулю.  В самом деле, если предположить, что потенциал создан точечной массой (или идеальным шаром) с массой М, то Возьмем градиент от выражения (2.3): От выражения (2.4) перейдём к дивергенции: Лапласиан во внешнем пространстве равен нулю. Функцию, для которой лапласиан равен нулю, называют гармонической. Равенство (2.5) говорит нам, что потенциал U во внешнем пространстве является гармонической функцией координат притягиваемой точки. Однако для масс находящихся внутри притягиваемого шара, за которую принимают Землю, Лапласиан не равен нулю. Пуассоном было доказано, что для точек, находящихся внутри, справедливо уравнение вида Уравнение Пуассона устанавливает связь между вторыми производными потенциала объемных масс для точки находящейся внутри этих масс и плотностью в этой точке. Таким образом, теория поля заключается в теории и методах решения линейных дифференциальных уравнений второго порядка (2.2) и (2.6), то есть уравнений Лапласа и Пуассона. Нам необходимо найти функцию U из решения (2.2) или (2.6). Заметим, что первые интегралы будут давать нам ÑU, то есть векторную функцию. Такая постановка задачи только с первого взгляда, кажется простой. На самом деле она таит в себе ряд проблем, которые не имеют однозначного решения. Заметим, что уже само решение дифференциальных уравнений сопряжено со значительными трудностями, т.к. решение дифференциальных уравнений с частными производными сводится к решению характеристических уравнений. При этом приходиться решать комбинации характеристических уравнений по переменным x, y, z. И таких комбинаций уравнений три: ((x, y), (x, z), (y, z)). Но если мы имеем дело с уравнениями второго порядка, то нетрудно сообразить, что каждое уравнение будет давать 9 комбинаций уравнений. Поэтому задачу напрямую “в лоб”, как правило, не решают, а находят всевозможные условия, вытекающие из физической сущности с тем, чтобы упростить ее решение. Это первая проблема, но не главная. Главная проблема заключается в следующем: сколько необходимо иметь точек внутри притягивающего тела и вне его с тем, чтобы однозначно и с заданной точностью определить функцию Третья немаловажная проблема: какого характера информация должна быть известна в этих точках, то есть, какого рода измерения необходимо выполнить в этих точках, чтобы надежно найти U и ÑU. А для измерений любого вида, как видим, сразу же возникают трудности в решении задачи Пуассона: физической возможности располагать измерениями внутри тела, мы не имеем даже для Земли, не говоря уже о других телах солнечной системы. Помимо самих измерений в уравнении Пуассона в правой части стоит еще и плотность d, которая должна быть известна в каждой точке внутри Земли. Что тоже проблематично. Поэтому уравнение (2.2), (2.6) решают не по начальным условиям (задача Коши), а по граничным или как принято говорить в теории фигуры Земли по «краевым условиям». То есть, решая уравнения Пуассона, располагают измерением на границе притягивающего тела, т.е. на его поверхности. Уравнения Лапласа решают под условием регулярности функции U и ÑU, т.е., что бы
Краевые задачи при определении потенциала В XIX веке английским ученым Стоксом было доказано, что U и ÑU однозначно определяются, если известны: 1. масса притягивающего тела m, 2. угловая скорость w притягивающего тела, 3. уровенная поверхность силы тяжести, внутри которой заключены все притягивающие массы тела m. Поэтому в дальнейшем решение задачи по определению U и ÑU получило название проблемы Стокса. Как следует из третьего условия, должна быть известна уровенная поверхность силы тяжести. Проблема Стокса строгого решения принципиально иметь не может и решена она только для простейших фигур (сферы, эллипсоида вращения, трехосного эллипсоида). Дальнейшее развитие проблемы Стокса привело к трем типам краевых задач: Первая краевая задача – задача Дирихле. Если в произвольных точках Pi замкнутой поверхности s функция U(Pi) принимает значения То есть, ставиться задача: по заданным значениям - внутренняя, когда U(r) существует в конечной области R ограниченной поверхности s, то есть - внешняя, когда U(r) существует во внешней области по отношению к s, то есть для Вторая краевая задача – задача Неймана. Если на поверхности s заданы значения нормальной производной Задача Неймана подразделяется тоже на две: внешняя и внутренняя в зависимости от того, где ищут решение внутри или вне поверхности s. Третья краевая задача – смешанная задача. В этой задаче на поверхности s должны быть заданы комбинации значений Задача также может быть внешней и внутренней. При определении функций U(r) и ÑU(r) всеми тремя краевыми задачами мы будем касаться только внешних задач, при этом ставиться обязательное условие, чтобы искомая гармоническая функция U(r) и ÑU(r) обращались на бесконечности в 0 (были регулярными). Внешние задачи рассматриваются еще и потому, что потенциал притяжения U(r) – функция гармоническая только во внешнем пространстве и, следовательно, при использовании для решения задачи уравнение Лапласа, мы можем использовать краевое условие только для внешней задачи. Внешние краевые задачи. Дифференциальное уравнение Лапласа (2.2) дает решение для всех вышеперечисленных задач в следующем виде. Первая задача Дирихле: где Вторая задача Неймана дает решение в виде где Третья смешанная задача имеет решение в виде где В заключение зададимся следующим вопросом: какие величины необходимо измерять, чтобы получить значение потенциала силы тяжести W. С этой целью возьмём производную в произвольной точке Р по произвольному направлению s. где Отметим, что элемент нормали dh к поверхности геоида в точке Р направлен в противоположном направлении к вектору Получив из (2.13) ds и подставив его в (2.12),имеем следующее выражение Интегрируя (2.14) от точки Р до произвольной точки Q, имеем Кроме того, для подынтегрального выражения имеем Из полученных выражений следует, что разность потенциалов WP – WQ между двумя точками Р и Q, находящимися на конечном расстоянии друг от друга есть интегральная сумма измеренных ускорений силы тяжести умноженное на превышения в каждой точке маршрута PQ и эта формула отвечает на вопрос: какие величины надо измерять, чтобы определить потенциал силы тяжести? Перечислим те методы, которые основаны на измерениях модуля ускорения силы тяжести и превышений в каждой измеряемой точке на земной поверхности: 1. Классический метод определения потенциала непосредственно следует из формулы (2.15)–необходимо по всему земному шару выполнить точечные измерения значений модуля ускорения силы тяжести 2. Методы, основанные на осреднении вышеперечисленных измерений по площадям (трапециям). Это метод Гаусса–Неймана и его современные модификации используют методы численного интегрирования. 3. Метод спутникового нивелирования (спутниковая альтиметрия) состоит в том, что положение спутника (из теории) и его высота над водной поверхностью (из измерений) должны быть известны с одинаковой точностью. А так как водная поверхность Земли (составляет около 80%) в спокойном состоянии представляет собой геоид, то за один оборот спутника получают глобальную (для всей Земли) трассу превышений геоида, а за 2–3 месяца плотно покрывают трассами всю акваторию мирового океана. Обработка этих измерений и дает нам поверхность геоида, то есть потенциал на поверхности Земли. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 657. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , которую именуют потенциалом, а также методы определения векторной функции
, которую именуют потенциалом, а также методы определения векторной функции  по заданным краевым условиям.
по заданным краевым условиям.

 (2.3)
(2.3)

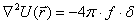 (2.6)
(2.6)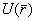 и ее градиент
и ее градиент  . Как следует из сущности задачи таких точек необходимо иметь, как можно больше, и они должны быть равномерно расположены, как внутри тела, так и вне его. Так можно вкратце сформулировать вторую главную проблему.
. Как следует из сущности задачи таких точек необходимо иметь, как можно больше, и они должны быть равномерно расположены, как внутри тела, так и вне его. Так можно вкратце сформулировать вторую главную проблему.
 , то гармоническая функция
, то гармоническая функция  существует и она единственна.
существует и она единственна. , принимаемым на поверхности s, требуется найти гармоническую функцию (удовлетворяющую уравнению Лапласа) –
, принимаемым на поверхности s, требуется найти гармоническую функцию (удовлетворяющую уравнению Лапласа) –  ;
; т.е. задан модуль силы тяжести и требуется найти значения функции U(r) в области ограниченной поверхностью s при этом функция U(r) должна быть гармоническая и регулярная на бесконечности.
т.е. задан модуль силы тяжести и требуется найти значения функции U(r) в области ограниченной поверхностью s при этом функция U(r) должна быть гармоническая и регулярная на бесконечности.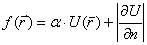 . По этим значениям требуется отыскать гармоническую функцию U(r).
. По этим значениям требуется отыскать гармоническую функцию U(r).
 , а функция G, получившая название функции Грина, обращается в нуль на поверхности s, т.е.
, а функция G, получившая название функции Грина, обращается в нуль на поверхности s, т.е.  . Произвольная функция Х(r) является гармонической и регулярной на бесконечности.
. Произвольная функция Х(r) является гармонической и регулярной на бесконечности.
 но, в отличие от функции Грина G, функция
но, в отличие от функции Грина G, функция  должна подчинятся условию
должна подчинятся условию 

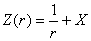 является произвольной функцией гармоничной и регулярной на бесконечности, которая находится из условия
является произвольной функцией гармоничной и регулярной на бесконечности, которая находится из условия 

 – единичный радиус–вектор. Будем полагать, что он совпадает с ускорением силы тяжести
– единичный радиус–вектор. Будем полагать, что он совпадает с ускорением силы тяжести  , поэтому
, поэтому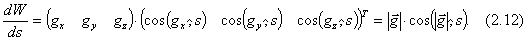
 . (2.13)
. (2.13) . (2.14)
. (2.14)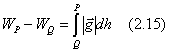

 и превышений dh. Эти работы выполняются гравиметрическими и нивелирными измерениями.
и превышений dh. Эти работы выполняются гравиметрическими и нивелирными измерениями.