
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формула включений и исключений⇐ ПредыдущаяСтр 20 из 20 Пусть имеется N предметов, каждый из которых может обладать свойствами а Обозначим через N(а Число предметов, не обладающих ни одним из указанных свойств, Обозначают по этому правилу через N(
Здесь алгебраическая сумма распространена на все комбинации свойств а Например, Примеры решения некоторых комбинаторных задач Задача. Из 28 студентов группы 14 человек занимаются плаванием, 18 человек – баскетболом, 12 студентов – легкой атлетикой, 8 – плаванием и баскетболом, 7 – легкой атлетикой и баскетболом, 6 – плаванием и легкой атлетикой, 3 студентов занимаются и плаванием, и баскетболом, и легкой атлетикой. Сколько в группе студентов, которые не занимаются ни одним из данных видов спорта?  Решение.Обозначим через p − увлечение плаванием, через b − увлечение баскетболом, через a − увлечение легкой атлетикой. Подсчитаем, сколько студентов в данной группе не занимаются ни одним из данных видов спорта, то есть найдем чему равно N( По условию задачи имеем N(p)=14, N(b)=18, N(a)=12, N(pb)=8, N(ba)=7, N(pa)=6, N(pba)=3. Значит, по формуле включений и исключений получаем, что N( Ответ: 2 студента не занимаются ни одним из данных видов спорта. Решите задачи, предложенные на странице 28, с помощью формулы включений и исключений. Задача. Сколькими способами можно отправить 8 различных фотографий, использовав при этом 5 различных конвертов? Решение.Решим задачу, используя формулу включений и исключений. Найдем сначала, при скольких способах распределения данные k конвертов оказываются пустыми (а остальные могут быть как пустыми, так и содержать фотографии). В этом случае фотографии кладутся без ограничений в (5−k) конвертов, число таких распределений равно Отсюда, применяя формулу включений и исключений, выводим, что число распределений, при которых ни один конверт не оказывается пустым, равно
Ответ: 126000 способами. Общая задача: сколькими способами можно положить п различных предметов в т различных ящиков так, чтобы в каждом ящике лежал хотя бы один предмет, решается точно такими же рассуждениями. Число способов распределения выражается формулой:
Пусть имеются Число способов распределения выражается формулой:
Задача. Необходимо разделить 8 яблок, 10 груш и 7 апельсинов между 4 ребятами, при этом каждый должен получить хотя бы один фрукт. Сколькими способами можно это сделать? Решение.Число способов распределения фруктов между детьми выражается формулой:
Ответ: 5239688 способами. До сих пор, раскладывая предметы по ящикам, мы не учитывали порядок, в котором могут быть расположены предметы в каждом ящике. Но, например, если речь идет о развешивании сигнальных флагов на мачтах, то имеет значение и порядок вывешиваемых флагов. Решим следующую задачу. Задача. Имеется n различных сигнальных флагов и m мачт, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке развешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми? Решение.Каждый способ развешивания флагов является комбинацией двух этапов. Первый − определение конфигурации, то есть мест, на которых будут висеть n флагов на m мачтах. На этом этапе не учитывается ни форма, ни окраска флага, все флаги считаются одинаковыми. Тогда, как мы уже знаем, п флагов можно развесить на m различных мачтах Второй этап − заполнение всех этих n мест конкретными флагами. Это можно сделать n! способами, потому что можно заполнить эти n мест флагами произвольным образом, а потом переставлять флаги друг с другом всевозможными способами, не меняя конфигурации. Число таких перестановок равно n!. Значит, для каждой конфигурации размещения флагов получается n! конкретных способов развешивания флагов. Общее же число способов развешивания флагов равно:
Вообще, если имеется n различных предметов, то число способов распределения этих предметов по m различным ящикам с учетом порядка их расположения в ящиках равно 28. Сколькими способами можно расставить 20 разных книг в книжном шкафу с 5 полками, если каждая полка может вместить все 20 книг? 29. Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?
Большой класс комбинаторных задач, важных в прикладной математике, сводится к подсчету числа тех или иных расстановок ладей на шахматной доске. Ладья является самой распространенной фигурой в комбинаторных задачах на шахматной доске и часто упоминается даже в серьезной математической литературе. Задачи о расположении фигур на шахматной доске можно рассматривать как задачи о раскладках. Здесь элементы (фигуры) могут быть различными или одинаковыми, все «ящики» (поля доски) различны, но есть причудливые ограничения в виде связи различных полей. Цикл комбинаторных задач на шахматной доске связан с подсчетом числа расположений шахматных фигур, при которых они могут бить друг друга или, наоборот, не могут бить друг друга. Приведем один известный пример из области комбинаторики. Задача. Пусть требуется назначить n рабочих на n различных работ, причем каждая работа должна выполняться только одним рабочим. Сколькими способами можно осуществить такое назначение? Решение.Поставим в соответствие рабочим − горизонтали шахматной доски n×n, а работам − ее вертикали. Если i-й рабочий назначается на j-ю работу, то поле, соответствующее пересечению i-й горизонтали и j-й вертикали, займем ладьей. Так как каждая работа выполняется одним рабочим и каждый рабочий назначается на одну работу, то в результате расстановки n ладей все вертикали и горизонтали доски будут содержать по одной ладье, то есть ладьи не могут бить друг друга. Итак, задаче о назначении можно придать шахматную формулировку. Задача. Сколькими способами можно расставить n ладей, которые не могли бы бить друг друга, на доске размера n×n? Решение.Заметим, что при любом расположении более n ладей найдется хотя бы одна вертикаль и хотя бы одна горизонталь с двумя или более ладьями, то есть n − это наибольшее число мирных ладей на доске n×n. Одна из расстановок восьми мирных ладей на обычной доске приведена на рисунке 8. Выясним например, сколько всего существует искомых расстановок n ладей на доске n×n. На первую вертикаль можно произвольно поставить одну из n ладей затем на вторую вертикаль − одну из (n-1) оставшихся ладей, причем горизонталь, занятая первой ладьей исключается (ладьи не должны угрожать друг другу) на третью вертикаль − одну из (n-2) оставшихся (горизонтали, занятые первыми двумя ладьями, исключаются) и т.д., вплоть до (n-1)-й вертикали, на которой для ладьи остается выбор из двух горизонталей, и последней, n-й вертикали, с единственным полем для ладьи. Комбинируя n различных расположений ладьи на первой вертикали с (n-1) расположением на второй, (n-2) − на третьей и т.д., получаем n(n-1)∙…∙2·1=n! различных расположений ладей. Это число и является искомым. В частности, на обычной доске восемь ладей, не угрожающих друг другу, можно расположить 8!=40320 способами. Если ладьи занумерованы числами от 1 до n, то существует уже (n!)2 расположений ладей, не угрожающих друг другу. Это следует из того, что n подходящих полей можно выбрать n! способами; столько же способов имеется для расположения на этих полях n занумерованных ладей. Итак, n рабочих можно назначить на n работ n! различными способами. Пусть выбрано назначение, соответствующее рисунку 7, то есть i-го рабочего назначили на i-ую работу, и требуется сделать новое назначение с учетом того, что каждый рабочий хочет поменять свою предыдущую работу. Сколько существует таких назначений? Эта задача имеет иную ладейную формулировку. Задача. Сколькими способами можно расставить n не угрожающих друг другу ладей на доске n×n так, чтобы ни одна из них не стояла на главной диагонали? Решение.Дополнительное условие значительно затрудняет решение задачи. Даже Эйлеру не удалось найти общую формулу для числа указанных расстановок. Позднее была найдена формула, которая имеет следующий вид: Для n=8 получаем 4833, то есть при дополнительном условии число расстановок восьми ладей, не угрожающих друг другу, уменьшается почти втрое. Задача. Сколькими способами можно расставить k ладей на m×n доске так, чтобы, они не могли бить друг друга. Решение.Ясно, что для разрешимости задачи нужно, чтобы выполнялись условия k<m и k<n − иначе какие-то две ладьи попадут на одну и ту же горизонталь или вертикаль. Пусть эти условия выполнены. Тогда расстановку ладей можно осуществить в два этапа. Сначала выберем горизонтали, на которых будут стоять ладьи. Так как общее число горизонталей равно m, а надо выбрать k горизонталей, то выбор можно сделать Однако, k горизонталей и k вертикалей пересекаются по k Задача. Сколькими способами можно расставить три ладьи на обычной шахматной доске? Решение.Три ладьи на обычной шахматной доске можно расставить При к=т=п формула дает ответ n!. Еcли снять ограничение, что ладьи не могут бить друг друга, то ответ будет иной. Именно, нам надо было бы выбрать из m×n клеток любые kклеток. А это можно сделать Усложним теперь задачу о ладьях и потребуем, чтобы они не только не били друг друга, но еще симметрично стояли на доске. При этом получается много задач в зависимости от того, какое налагается условие симметрии. Самым простым является случай, когда требуется, чтобы ладьи стояли симметрично относительно центра доски (Рис.9) Обозначим через В самом деле, будем ставить 2n ладей на доску размера 2n×2n. Ладья, стоящая на первой вертикали, может занять на ней любое из 2n полей. По условию этим определяется положение ладьи, стоящей на последней вертикали − она должна расположиться симметрично с первой ладьей относительно центра доски. Вычеркнем первую и последнюю вертикали, а также занятые стоящими на них ладьями горизонтали (так как число горизонталей четно, выбрасываемые ладьи не могут стоять на одной и той же горизонтали) и, если горизонтали не крайние, то «сомкнем ряды» на доске. Получается ( А теперь рассмотрим случай, когда доска состоит из ( В рассмотренных задачах о ладьях, как и в аналогичных задачах для других фигур, обычно предполагается, что все они одного цвета. Если расставлять и белые, и черные фигуры, то число расстановок увеличивается. Задача. Сколькими способами можно расставить n мирных ладей на доске n×n, если k из них − белые и (n−k) − черные? Решение.Всякая расстановка, удовлетворяющая условиям задачи, определяется выбором n полей для всех n мирных ладей и затем указанием k полей из этих n, на которых будут расположены белые ладьи, остальные (n−k) полей займут черные ладьи. Таким образом, искомое число расстановок равно Рассмотрим снова расстановку на рисунке. Мы видим, что восемь ладей способны взять под обстрел все поля шахматной доски. Соответственно, для охраны всей доски n×n достаточно иметь n ладей. Если ладей меньше, чем n, то по крайней мере одна ее вертикаль и одна горизонталь окажутся пустыми и, значит, поле, стоящее на их пересечении, не будет атаковано. Сколькими способами можно расставить n ладей на доске n×n так, чтобы они держали под обстрелом все поля доски? Если n ладей охраняют доску, то либо на каждой вертикали, либо на каждой горизонтали стоит хотя бы одна из них (если существуют вертикаль и горизонталь, свободные от ладей, то поле, находящееся на их пересечении, не атаковано). Число расстановок i ладей − по одной на каждой вертикали равно nn (первую ладью можно поставить на одно из n полей первой вертикали; вторую, независимо от первой, на одно из n полей второй вертикали и т.д.). Столько же имеется расстановок и по одной на каждой горизонтали. На первый взгляд кажется, что общее число расположений ладей равно nn+nn=2nn. Однако при таком подсчете дважды учитываются расстановки, в которых на каждой вертикали и на каждой горизонтали стоит по одной ладье. Так как каждая из них характеризуется тем, что никакая пара ладей не угрожает друг другу, то решением задачи является число 2·nn−n!. Число расстановок восьми ладей, обстреливающих обычную доску, равно 2·88−8!=33514312. Комбинаторные задачи о расстановке атакующих фигур не менее популярны, чем задачи о расстановке мирных фигур. Наиболее просто они решаются для ладьи. 30. Сколькими способами можно расставить 4 мирных ладьи на доске 8×8, если 2 из них − белые и 2 − черные? 31. Сколькими способами можно расставить 8 ладей, которые не могли бы бить друг друга, на доске размера 8×8? 32. Сколькими способами можно расставить 4 ладьи на обычной шахматной доске? 33. Сколькими способами можно поставить 20 белых шашек на шахматной доске так, чтобы это расположение не менялось при повороте доски на 90°? Задачи для самостоятельного решения по курсу «Комбинаторика» 1. Сколько трехэлементных упорядоченных подмножеств можно составить из элементов шестиэлементного множества? 2. Сколько пятиэлементных подмножеств можно составить из элементов пятиэлементного множества? 3. Сколько кортежей длины 4 можно составить из элементов пятиэлементного множества? 4. Сколько подмножеств можно составить из элементов трехэлементного множества? 5. Имеется три аудитории на первом этаже, 4 – на втором этаже, 5 – на третьем этаже. Сколькими способами можно выбрать: а) три аудитории; б) одну аудиторию; в) три аудитории на разных этажах; г) три аудитории для занятий математикой, информатикой и музыкой; д) три аудитории на одном этаже; е) три аудитории так, чтобы хотя бы одна из них была на втором этаже? 6. Имеется 4 мяча, 5 кукол и 5 машинок. Сколькими способами можно выбрать: а) 3 разных игрушки; б) 3 игрушки; в) 1 игрушку; г) 3 игрушки для Коли, Сони, Тани; д) 3 одинаковых игрушки; е) 3 игрушки так, чтобы среди них было хотя бы 2 куклы? 7. Сколько 4-элементных упорядоченных подмножеств можно составить из элементов шестиэлементного множества? 8. Сколько пятиэлементных подмножеств можно составить из элементов четырехэлементного множества? 9. Сколько кортежей длины 3 можно составить из элементов трехэлементного множества? 10. Сколько подмножеств можно составить из элементов пятиэлементного множества? 11. В магазине, из произведений И. С. Тургенева имеется 6 экземпляров романа «Рудин», 3 экземпляра романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме этого, есть 5 томов, содержащих романы «Рудин» и «Дворянское гнездо», и 7 томов, содержащих романы «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному из этих романов? 12. Сколькими способами можно обить 6 различных стульев, если имеются 12 сортов обивочного материала? 13. Из 100 человек английский язык изучают 28, немецкий – 30, французский – 42, английский и немецкий –8, английский и французский – 10, немецкий и французский – 5. Все три языка изучают три студента. Сколько студентов изучает только один язык? Сколько студентов не изучает ни одного языка? Сколько студентов изучают только немецкий язык? 14. В школе 70 учеников. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора и 8 спортсменов. В хоре 6 спортсменов. 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не ходят в драмкружок? 15. Даны 40 чисел. Из них 10 чисел кратны трем, 15 чисел кратны двум, 20 чисел не кратны ни трем, ни двум. Сколько среди данных 40 чисел, кратных шести? 16. На уроке литературы учитель спросил, кто из 40 учеников класса читал книги А, В и С. Оказалось, что книгу А читали 25 учащихся, книгу В – 22, книгу С – также 22 учащихся. Книгу А или В читали 33 ученика, А или С – 32, В или С – 31. Все три книги прочли 10 учащихся. Сколько учеников прочли только одну книгу? Сколько учащихся не читали ни одной из этих трех книг? 17. Сколькими способами можно рассадить восемь гостей на восьми различных стульях? 18. В отделении 12 солдат. Сколькими способами можно составить наряд из трех человек? 19. Во взводе 5 сержантов и 50 солдат. Сколькими способами можно составить наряд из 1 сержанта и 3 солдат? Сколькими способами можно составить наряд из 2 сержантов и 5 солдат? 20. В классе 42 свободных места. Сколькими способами можно посадить на них 8 учеников? 26 учеников? 21. В комнате имеется 6 лампочек. Сколькими различными способами можно осветить комнату? 22. Имеется 5 видов конвертов без марок и 4 вида марок одного и того же достоинства. Сколькими способами можно выбрать конверт и марку для письма? 23. Сколькими способами можно выбрать на шахматной доске два квадрата – белый и черный? два белых квадрата? 24. Из 12 слов мужского рода, 9 женского и 10 среднего, надо выбрать по одному слову каждого рода. Сколькими способами может быть сделан этот выбор? 25. Из состава участников конференции, на которой присутствуют 18 человек, надо избрать делегацию, состоящую из 4 человек. Сколькими способами это можно сделать? 26. Имеется 6 книг А.С. Пушкина, 5 книг М.Ю.Лермонтова и 7 книг Л.Н.Толстого. Сколькими способами можно выбрать: а) 3 книги для Николая, Петра и Павла; б) 3 книги разных авторов; в) одну книгу; г) 3 книги; д) три книги одного автора; е) 3 книги так, чтобы среди них была по крайней мере одна книга А.С.Пушкина; е) по 3 книги каждого автора? 27. Сколько двухэлементных упорядоченных подмножеств можно составить из элементов шестиэлементного множества? 28. Сколько п-элементных подмножеств можно составить из элементов т-элементного множества? 29. Сколько подмножеств можно составить из элементов к-элементного множества? 30. Сколько п-элементных упорядоченных подмножеств можно составить из элементов т-элементного множества? 31. Сколько кортежей длины т можно составить из элементов п-элементного множества? 32. Сколько кортежей длины т можно составить из элементов т-элементного множества? 33. Сколько п-элементных упорядоченных подмножеств можно составить из элементов п-элементного множества? 34. В доме отдыха каждый день давали на десерт либо яблоко, либо апельсин, либо мандарин. В течение 24 дней было выдано 9 яблок, 7 мандаринов и 8 апельсинов. Сколько различных вариантов могло быть? 35. Сколькими способами можно составить трехцветный флаг (три горизонтальные полосы одинаковой ширины), если имеется материал 6 различных цветов? 36. Восемь авторов должны написать книгу из шестнадцати глав. Сколькими способами возможно распределение материала между авторами, если два человека напишут по три главы, четыре – по две и два – по одной главе книги? 37. Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов? 38. Садовник должен в течение трех дней посадить десять деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день? 39. Двенадцати ученикам выданы два варианта контрольно работы. Сколькими способами их можно посадить в два ряда, чтобы рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант? 40. Каждый из десяти радистов пункта А старается установить связь с каждым из двадцати радистов пункта Б. Сколько возможно различных исходов такой связи? 41. Шесть ящиков различных материалов доставляются на восемь этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на восьмой этаж будет доставлен какой-либо один материал? 42. Пятерых студентов следует распределить по трем группам. Сколькими способами это можно сделать? 43. Сколько трехзначных чисел, делящихся на 3, можно составить из цифр 0, 1,2, 3, 4, 5, если каждое число не должно содержать одинаковых цифр? 44. Собрание из 80 человек избирает председателя, секретаря и трех членов редакционной комиссии. Сколькими способами это можно сделать? 45. Четверо студентов сдают экзамен. Сколькими способами им могут быть поставлены отметки, если известно, что ни один из студентов не получит неудовлетворительной оценки? 46. Сколько чисел, меньших, чем миллион, можно записать с помощью цифр 9, 8, 7? 47. Сколько разных комбинаций ответов можно дать на 8 вопросов, если на каждый вопрос отвечают «да» или «нет»? 48. Из двух спортивных обществ, насчитывающих по 120 фехтовальщиков каждое, нужно выделить по одному фехтовальщику для участия в состязании. Сколькими способами может быть сделан этот выбор? 49. На вершину горы ведут 10 дорог. Сколькими способами турист может подняться на гору и спуститься с нее? Сколькими способами турист может подняться на гору и спуститься с нее, но при условии, что спуск и подъем происходят по разным путям. Решите задачу разными способами. 50. В классе четыре человека хорошо поют, двое других играют на гитаре, а еще двое умеют показывать фокусы. Сколькими способами можно составить концертную бригаду из гитариста и фокусника? Сколькими способами можно составить концертную бригаду из певца, гитариста и фокусника? Сколькими способами можно составить концертную бригаду из двух певцов и фокусника? Сколькими способами можно составить концертную бригаду из трех человек? Сколькими способами можно составить концертную бригаду из трех человек так, чтобы в нее входил хотя бы один певец? 51. Сколько чисел, больших 100, можно записать с помощью цифр 1, 2, 3, 4, если в одном числе каждая цифра используется не более одного раза? 52. Сколько чисел можно записать с помощью цифр 1, 2, 3, 4, если в одном числе каждая цифра используется не более одного раза? 53. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно. 54. Сколько четных чисел, меньших 500, можно составить с помощью цифр 2, 3, 4, 5, 6 так, чтобы ни в одном числе не было повторяющихся цифр? 55. Сколькими способами можно 6 девочек разбить на две команды по три девочки в каждой команде? 56. Сколькими способами можно заполнить карточку «Спортлото», зачеркнуть 6 номеров из 49? 57. Сколькими способами можно образовать из группы в 12 мужчин и 8 женщин комиссию, так чтобы она состояла из 3 мужчин и 4 женщин? 58. В фортепьянном кружке занимаются 10 человек, кружке художественного слова – 15, в вокальном кружке – 12 и в фотокружке – 20 человек. Сколькими способами можно составить бригаду из четырех чтецов, трех пианистов, пяти певцов и одного фотографа? Решите задачу разными способами. 59. Десять групп занимаются в десяти, расположенных подряд, аудиториях. Сколько существует вариантов расписания, при которых группы № 23 и № 22 находились бы в соседних аудиториях? Сколько существует вариантов расписания, при которых группы № 23 и № 22 не находились бы в соседних аудиториях? 60. Шесть ящиков различных материалов доставляются на пять этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на пятый этаж будет доставлено не менее двух материалов? 61. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу? 62. Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать? 63. Сколько различных слов можно получить, переставляя буквы в слове «кукушка»? 64. Сколькими способами можно расставить белые фигуры (2 коня, 2 слона, 2 ладьи, ферзь и король) на первой линии шахматной доски? 65. Две ладьи различного цвета расположены на шахматной доске так, что каждая может взять другую. Сколько существует таких расположений? (Одна ладья может взять другую, если она находится с ней на одной горизонтали или на одной вертикали шахматной доски.) 66. Сколькими способами можно расставить 12 белых и 12 черных шашек на 32 черных полях? 67. Сколькими способами можно расставить восемь книг в книжном шкафу с пятью полками, если каждая полка может вместить все восемь книг? 68. Сколькими способами можно расставить а книг в книжном шкафу с пятью полками, если каждая полка может вместить все а книг? 69. Сколько слов, состоящих из к букв, можно образовать из 32 букв алфавита? 70. Сколькими способами можно переставить буквы слова «перешеек» так, чтобы 4 буквы «е» шли подряд? 71. Двое ребят собрали 10 ромашек, 15 васильков и 14 незабудок. Сколькими способами они могут разделить между собой эти цветы? 72. Сколькими способами можно разделить 15 яблок между тремя мальчиками? 73. Сколькими способами можно разделить 15 яблок и 20 апельсинов между тремя мальчиками? 74. Шифр состоит из 4 цифр и 4 букв, причем буквы в записи шифра не повторяются. Буквы – я, ч, с, м, и, т. Сколькими способами можно составить этот шифр? 75. Имеется 5 юношей и 5 девушек. Сколькими способами можно разделить их на 2 команды по 5 человек так, чтобы в команде была хотя бы одна девушка? 76. Шифр состоит из 3 цифр или 5 букв. Буквы – а, п, р, о, л. Сколькими способами можно составить этот шифр? 77. Шифр состоит из 3 цифр и 5 букв. Сколькими способами можно составить этот шифр? 78. Шифр состоит из 3 цифр или 5 букв. Сколькими способами можно составить этот шифр? 79. Шифр состоит из 3 цифр или 5 букв, причем буквы в записи шифра не повторяются. Сколькими способами можно составить этот шифр? 80. Имеется 10 юношей и 12 девушек. Сколькими способами можно выбрать из них 5 пар для танца? 81. Из трех математиков и десяти экономистов надо составить комиссию в составе восьми человек. Сколькими способами может быть составлена комиссия, если в нее должен входить хотя бы один математик? 82. В купе железнодорожного вагона один против другого стоят два дивана, на каждом из которых по четыре места. Из восьми пассажиров трое желают сидеть лицом в направлении движения поезда, а два – спиной. Сколькими способами могут разместиться пассажиры, с учетом их пожеланий? 83. Для генетического эксперимента необходимо взять 4 белых, 7 красных и 5 розовых цветков гороха из имеющихся 10 белых, 10 красных и 10 розовых цветков гороха. Сколькими способами можно это сделать? 84. На книжной полке стоит собрание сочинений в 8 томов. Сколькими различными способами их можно переставить так, чтобы: а) тома 1 и 2 стояли рядом; б) тома 4 и 5 рядом не стояли? 85. Комплексная бригада состоит из 2 маляров, 3 штукатуров и 2 столяров. Сколько различных бригад можно создать из коллектива, в котором 15 маляров, 10 штукатуров и 5 столяров? 86. «Вороне где-то Бог послал кусочек сыра», брынзы, колбасы, сухарика и шоколада. «На ель Ворона взгромоздясь, позавтракать совсем уж было собралась, да призадумалась»: а) если съедать кусочки по очереди, то из скольких вариантов придется выбирать; б) сколько получится «бутербродов» из двух кусочков; в) если съесть сразу 3 кусочка, а остальные спрятать, то из скольких вариантов придется выбирать; г) сколько получится вариантов, если какой-то кусочек все-таки бросить Лисе, а потом ответить на вопрос пункта а)? 87. Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». Сколькими способами они могут: а) по одному сесть за выбранные четыре инструмента; б) выбрать 5 инструментов из 12 данных; в) по одному сесть за какие-то 4 из выбранных 5 инструментов из 12 данных; г) выгнать одного, не имеющего слуха, и потом сыграть на каких-то трех из выбранных 5 инструментов из 12 данных? 88. Из колоды в 36 карт вынимают 6 карт. Найдите: а) число всех возможных вариантов выбора; б) число вариантов, при которых среди полученных карт есть 4 туза; в) число вариантов, при которых все полученные карты – пики; г) число вариантов, при которых все полученные карты – одной масти. Решите данную задачу для колоды 54 карт. 89. По списку в группе 26 студентов, из них18 девушек. нужно выбрать двух дежурных по аудитории. Сколькими способами это можно сделать: а) при условии, что пару обязательно должны составить две девушки; б) при условии, что пару обязательно должны составить девушка и парень; в) без указанных условий; г) при условии, что в пару обязательно должна входить хотя бы одна девушка? 90. По списку в группе 26 студентов, из них18 девушек. Нужно выделить группу из трех человек для участия в конкурсе. Сколькими способами это можно сделать, если: а) все члены этой группы должны быть девушками; б) все члены этой группы должны быть парнями; в) в группе должны быть 1 девушка и 2 парня; г) в группе должен быть хотя бы 1 парень; д) в группе должны быть хотя бы 2 девушки? 91. В оперном театре 12 певцов и 10 певиц, а в опере по замыслу композитора 5 мужских и 3 женских партии. Сколько существует различных певческих составов для спектакля, если известно, что: а) певцы А и Б ни за что не будут петь вместе; б) певец А будет петь тогда и только тогда, когда будет петь певица В; в) все певцы и певицы прекрасно ладят между собой? 92. В чемпионате России по футболу в высшей лиге участвуют 16 команд. Перед началом чемпионата газета «Спорт» провела Интернет-опрос читателей, задав им два вопроса: 1) какая команда получит золотые, какая – серебряные и какая – бронзовые медали? 2) какие две команды окажутся среди неудачников, то есть займут два последних места? Читатели в своих ответах указали все возможные варианты и при ответе на первый, и при ответе на второй вопросы. Сколько вариантов состава неудачников указали участники опроса? Сколько из них тех, в которые входит команда «Динамо»? Сколько вариантов тройки призеров указали участники опроса? Сколько из них тех, в которые входят «Спартак» и «Зенит»? 93. Имеется 25 рабочих, 5 маляров, 4 плотника и 3 штукатура. Сколькими способами можно укомплектовать бригаду из 5 человек так, чтобы в нее вошли ровно по одному маляру, плотнику и штукатуру? Сколькими способами можно укомплектовать бригаду из 5 человек так, чтобы в нее вошло не менее двух маляров? 94. Среди 25 рабочих – 5 маляров, 4 плотника и 3 штукатура. Сколькими способами можно укомплектовать бригаду из 5 человек так, чтобы в нее вошли ровно по одному маляру, плотнику и штукатуру? Сколькими способами можно укомплектовать бригаду из 5 человек так, чтобы в нее вошло не менее двух маляров? 95. Из 10 роз и 8 георгинов нужно составить букет. Сколько можно составить различных букетов, содержащих 2 розы и 3 георгина? Сколько можно составить различных букетов, содержащих не менее 2 роз? 96. Из 6 чайных чашек, 6 блюдец и 6 чайных ложек хотят сервировать стол на 3 персоны, положив каждой из них 1 чашку, 1 блюдце и 1 ложку. Сколькими способами можно это сделать? 97. В корзине находится 10 белых и 7 черных шаров. Сколькими способами можно выбрать из корзины 5 шаров, из которых белыми будут 3 штуки? 98. Обобщите решение задачи 95 на случай наличия т белых шаров и п черных шаров. Из корзины выбирается г шаров, из которых k штук белых. 99. В корзине находится 10 белых и 7 черных шаров. Сколькими способами можно выбрать из корзины 5 шаров, так, чтобы все они были черными? Сколькими способами можно выбрать из корзины 5 шаров, из которых 3 должны быть одного цвета? Сколькими способами можно выбрать из корзины 5 шаров, так, чтобы все они были одного цвета? Сколькими способами можно выбрать из корзины 5 шаров, из которых хотя бы 3 должны быть белыми? Сколькими способами можно выбрать из корзины 5 шаров так, чтобы черными были не более трех шаров? 100. Из 5 различных чайных чашек, 5 блюдец и 5 чайных ложек хотят сервировать стол на три персоны, положив каждой из них одну чашку, одно блюдце и одну ложку. Сколькими способами можно это сделать? 101. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и той же горизонтали и вертикали? 102. Имеется 5 юношей и 5 девушек. Сколькими способами можно разделить их на 2 команды по 5 человек так, чтобы в команде была хотя бы одна девушка? 103. На собрании должны выступить 5 человек: А, Б, В, Г, Д. а) Сколькими способами можно расположить их в списке выступающих? б) Сколько существует вариантов порядка выступлений, при которых Б выступает после А? в) Сколько существует вариантов порядка выступлений, при которых Б выступает непосредственно после А? 104. Выберите самостоятельно число членов некоторого комитета. Минимальный кворум для принятия решения этим комитетом должен быть не менееего состава. Определите, сколькими способами можно достичь минимального кворума. 105. В лабораторной клетке находятся 8 белых и 6 коричневых кроликов. Найдите число способов выбора шести кроликов из клетки, если: а) они могут быть любого цвета; б) 3 из них должны быть белыми, а 3 коричневыми; в) все 6 кроликов должны быть белыми; г) все 6 кроликов должны быть одного цвета; д) хотя бы 1 из них должен быть белым; е) не более двух должны быть белыми? 106. В первые 3 вагона поезда садятся 9 пассажиров по 3 человека в каждый вагон. Сколькими способами можно это сделать? 107. Сколько можно составить семизначных телефонных номеров из цифр пятеричной системы счисления так, чтобы в каждом отдельно взятом номере все цифры были различны? 108. За стол рассаживают п гостей. Сколько существует способов это сделать при условии, что два гостя – А и Б – не должны сидеть рядом? 109. В школьной лотерее на 50 билетов разыгрывается 8 выигрышей. Первый подошедший к урне ученик выбирает из урны 5 билетов. Сколькими способами он может их вынуть, чтобы: а) среди них оказалось 2 выигрышных; б) по крайней мере, 2 из них оказались выигрышными? 110. На некоторой плоскости п параллельных прямых пересекаются т параллельными прямыми. Сколько параллелограммов можно выделить в образовавшейся сетке? 111. Задача Леонарда Эйлера. Трое господ при входе в ресторан отдали швейцару свои шляпы, а при выходе получили их обратно. Сколько существует вариантов, при которых каждый из них получит чужую шляпу? 112. Имеется ткань двух цветов: голубого и зеленого, и требуется обить диван, кресло и 2 стула. Сколько существует различных вариантов обивки этой мебели? 113. Из 42 вопросов к экзамену студент Кирилл Савельев 23 вопроса выучил, 8 совсем не смотрел, а в остальных что-то знает, а что-то нет. На экзамене в билете будет три вопроса. а) Сколько существует вариантов билетов? б) Сколько из них тех, в которых Савельев знает все вопросы? в) Сколько из них тех, в которых есть вопросы всех 3 типов? г) Сколько из них тех, в которых Савельев выучил большинство вопросов? [1] Тонких А.В. Математика. −М. Университет. Книжный дом, 2002, с.151. [2] Энциклопедия для детей. Том11.Математика. «Авнта+», 2000, с.249. [3] Пуанкаре А., О науке. −М. Наука, 1983, с.294. [4] Виленкин Н.Я. Популярная комбинаторика. −М., Наука, 1975. [5]В 213 г. до н. э. император Цин-Ши-Хуан приказал сжечь все книги, поэтому до нас дошли копии рукописей, которые были сделаны уже намного позже. [6]Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. −М.:ФИМА МЦНМО,2006, с.305. [7]Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. −М.:ФИМА МЦНМО,2006, с.311. [8]Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. −М.:ФИМА МЦНМО,2006, с.311. [9] Паскаль Блез (1623-1662) − выдающийся математик, физик, философ и писатель, один из самых знаменитых людей в истории человечества. Его именем названа единица давления (паскаль) и популярный язык программирования. Одной из наиболее популярных математических работ Б.Паскаля является «Трактат об арифметическом треугольнике, образованном биноминальными коэффициентами» (треугольник Паскаля). [10] Ферма Пьер (1601-1665) − французский математик, создатель теории чисел и один из основателей математического анализа. С именем Ферма связаны две знаменитые теоремы из области теории чисел: малая теорема Ферма и «великая» теорема Ферма, о которой на полях трудов Диофанта он написал: «Я нашел этому поистине чудесное доказательство, но эти поля слишком малы для него». [11] Лейбниц Готфрид Вильгельм (1646-1716) – немецкий философ, математик, физик, один из создателей дифференциального исчисления. [12] Эйлер Леонард (1707-1783) – математик, механик, физик и астроном, по происхождению швейцарец. Работал в России и в Германии. Автор более 800 работ по математическому анализу, теории чисел, дифференциальной геометрии и др. [13] Тонких А.В. Математика. −М., Университет. Книжный дом, 2002, с.161. [14] Энциклопедия для детей. Т.11.Математика.−М.«Аванта +», 2000, с.249. [15] Виленкин Н.Я. Алгебра. М., Просвещение, 1996. [16] Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. −М.:ФИМА МЦНМО, 2006, с.62-119. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1595. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,а
,а  ,...,а
,...,а 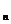 . При этом каждый предмет может обладать одним или несколькими свойствами, а может не обладать ни одним из этих свойств.
. При этом каждый предмет может обладать одним или несколькими свойствами, а может не обладать ни одним из этих свойств. а
а  …а
…а 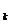 ) количество предметов, обладающих свойствами а
) количество предметов, обладающих свойствами а 

 ) обозначено количество предметов, обладающих свойствами
) обозначено количество предметов, обладающих свойствами  (вопрос об остальных свойствах остается открытым).
(вопрос об остальных свойствах остается открытым).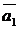
 …
…  ). Общий закон состоит в том, что
). Общий закон состоит в том, что
 входит со знаком «+», а
входит со знаком «+», а 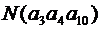 − со знаком «−». Формулу (*) называют формулой включений и исключений − сначала исключаются все предметы, обладающие хотя бы одним из свойств а
− со знаком «−». Формулу (*) называют формулой включений и исключений − сначала исключаются все предметы, обладающие хотя бы одним из свойств а  ).
).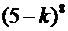 . Но kконвертов можно выбрать из пяти
. Но kконвертов можно выбрать из пяти 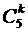 способами.
способами.
 Рассмотрим общее утверждение.
Рассмотрим общее утверждение. , предметов первого вида,
, предметов первого вида,  предметов второго вида, …,
предметов второго вида, …,  предметов k-го вида. Сколькими способами можно раздать их т лицам так, чтобы каждый получил хотя бы один предмет?
предметов k-го вида. Сколькими способами можно раздать их т лицам так, чтобы каждый получил хотя бы один предмет?

 способами.
способами.
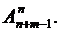
 Рис.8
Рис.8 .
. способами. Точно так же вертикали, на которых будут стоять ладьи, можно выбрать
способами. Точно так же вертикали, на которых будут стоять ладьи, можно выбрать  способами. Поскольку выбор вертикалей не зависит от выбора горизонталей, то поправилу произведения получаем
способами. Поскольку выбор вертикалей не зависит от выбора горизонталей, то поправилу произведения получаем 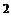 клеткам. Сдвигая, если понадобится, эти горизонтали и вертикали, мы получим новую доску из k горизонталей и k вертикалей. На такой доске расставить k ладей так, чтобы они не могли бить друг друга, можно k! способами. Поэтому общее число требуемых расположений ладей равно
клеткам. Сдвигая, если понадобится, эти горизонтали и вертикали, мы получим новую доску из k горизонталей и k вертикалей. На такой доске расставить k ладей так, чтобы они не могли бить друг друга, можно k! способами. Поэтому общее число требуемых расположений ладей равно 
 способами.
способами. способами. А если бы kладей различались друг от друга, то полученные ответы надо было бы еще умножить на k!.
способами. А если бы kладей различались друг от друга, то полученные ответы надо было бы еще умножить на k!. Рис.9
Рис.9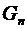 число решений задачи, когда n ладей стоят на доске из n горизонталей и n вертикалей. Тогда имеет место рекуррентное соотношение
число решений задачи, когда n ладей стоят на доске из n горизонталей и n вертикалей. Тогда имеет место рекуррентное соотношение  .
. ) горизонталей и (
) горизонталей и (  ) горизонталей и вертикалей. В этом случае одна ладья обязана стоять в центре доски. Поле, которое она занимает, само себе симметрично. Вычеркивая центральные горизонталь и вертикаль, получаем доску размера 2n×2n, на которую предстоит поставить 2n ладей, что можно сделать
) горизонталей и вертикалей. В этом случае одна ладья обязана стоять в центре доски. Поле, которое она занимает, само себе симметрично. Вычеркивая центральные горизонталь и вертикаль, получаем доску размера 2n×2n, на которую предстоит поставить 2n ладей, что можно сделать 
 способами. Значит,
способами. Значит, 
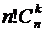 .
.