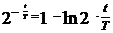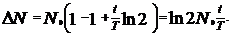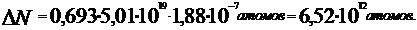Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Квантовая физика. Радиоактивность.Основные формулы: Энергия фотона: где Масса фотона:
Импульс фотона:
Уравнение Эйнштейна для внешнего фотоэффекта:
Где m - масса электрона; Закон Стефана- Больцмана:
Где
Закон Смещения Вина:
Где Основной закон радиоактивного распада:
Где Зависимость периода полураспада от постоянной радиоактивного распада:
Среднее время жизни радиоактивного ядра, т.е. промежуток времени, за который число не распавшихся ядер уменьшается в
Активность радиоактивного изотопа:
Где ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПРИМЕР №1.Определить кинетическую энергию Решение. Кинетическую энергию фотоэлектронов определим из формулы Эйнштейна для фотоэффекта:
Где  Из формулы (1) следует:
Частоту света определим по формуле:
Где Если поверхность металла освещать лучами частотой
Где Подставим во (2) выражение для
Выпишем числовые значения величин в СИ:
Проверим единицы измерения правой и левой частей формулы (5):
Произведем вычисления:
Из формулы Определяем скорость фотоэлектронов:
Выпишем числовые значения и произведем вычисления:
ПРИМЕР №2 Максимум энергии излучения абсолютного черного тела при некоторой температуре приходится на длину волны Решение. Энергетическая светимость абсолютно черного тела определяется по формуле: Где Абсолютную температуру определим из закона смещения Вина:
откуда где Подставим выражение для Выпишем числовые значения в СИ:
Проверим единицы измерения правой и левой частей формулы (3):
Произведем вычисления:
Энергию, излучаемую с площади
Выпишем числовые значения в СИ:
Проверим единицы измерения правой и левой частей формулы(4):
Произведем вычисления:
Массу
Где Выпишем числовые значения величин и вычислим массу:
ПРИМЕР №3 Какую мощность нужно подводить к свинцовому шарику радиусом 4 см, чтобы поддерживать его температуру при Дано: Найти: Решение. По закону Стефана – Больцмана для абсолютно черного тела энергетическая светимость равна
Где Энергию, излучаемую с площади поверхности шара
Но так как излучение происходит в среду с температурой Подставляя численные значения, вычисляем
Проверяем единицу измерения ПРИМЕР №4 Сколько атомов радиоактивного натрия РЕШЕНИЕ Число
где N - число атомов, не распавшихся к моменту времени t Но число атомов, не распавшихся к моменту времени t, выражается законом радиоактивного распада, т. е.
Где С учетом этого равенство (1) примет следующий вид:
Преобразуем в этой формуле выражение
так как После такого преобразования формула (3) примет вид:
Вычислим входящее в эту формулу число N0. Число атомов N0, содержащихся в некоторой массе m вещества, равно произведению числа Авогадро на количество вещества m/µ, т. е. N0=N ·m/µ В данном случае m = 2мг = 2·10-6кг и µ=24·10-3кг, поэтому N0=6,022·1023·2·10-6/24·10-3=5,01·1019атомов. Теперь можно определить число атомов, распадающихся за указанные в условии задачи промежутки времени. Для вычисления числа атомов, распадающихся за время, равное 10ч, можно применить непосредственно формулу (4). Подставив в нее числовые значения величин N0= 5,01·1019атомов и Т=14,8ч = 5,33·104с, получим:
Пользоваться формулу (4) для определения числа атомов, распадающихся за время, равное 0,01с, не следует, так как в этом случае вычисление выражения
весьма затруднительно. Поэтому вместо формулы (4) получим приближенную формулу. Для этого разложим в ряд выражение Из математики известно, что
Следовательно,
Но ввиду малости Тогда И выражение (4) примет вид:
Подставив сюда числовые значения величин, получим:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 669. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
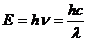 ,
,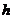 - постоянная Планка;
- постоянная Планка;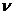 - частота света;
- частота света;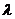 - длина волны;
- длина волны;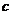 - скорость света в вакууме.
- скорость света в вакууме.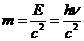 .
.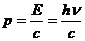 .
.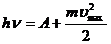 ,
,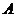 - работа выхода электрона из металла;
- работа выхода электрона из металла;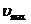 - максимальная скорость электрона.
- максимальная скорость электрона.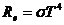 ,
,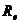 - энергетическая светимость абсолютно чёрного тела;
- энергетическая светимость абсолютно чёрного тела;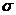 - постоянная Стефана – Больцмана
- постоянная Стефана – Больцмана - термодинамическая температура.
- термодинамическая температура.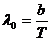 ,
,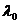 - длина волны, на которую приходится максимум энергии излучения;
- длина волны, на которую приходится максимум энергии излучения;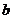 - постоянная Вина.
- постоянная Вина.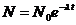 ,
,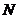 - число ядер, не распавшихся к моменту времени
- число ядер, не распавшихся к моменту времени 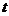 ;
;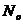 - число ядер в начальный момент времени
- число ядер в начальный момент времени 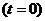 ;
;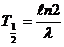
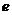 раз:
раз: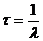
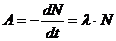 , или
, или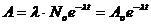 ,
,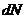 - число ядер, распадающихся за интервал времени
- число ядер, распадающихся за интервал времени 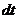 ;
;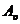 - активность изотопа в начальный момент времени.
- активность изотопа в начальный момент времени.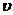 фотоэлектронов при облучении натрия лучами длиной волны
фотоэлектронов при облучении натрия лучами длиной волны 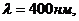 если красная граница (порог) фотоэффекта для натрия
если красная граница (порог) фотоэффекта для натрия 
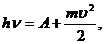 (1)
(1)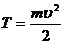 - кинетическая энергия фотоэлектронов,
- кинетическая энергия фотоэлектронов,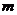 - масса электрона,
- масса электрона,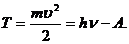 (2)
(2)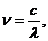 (3)
(3)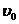 , соответствующей красной границе фотоэффекта, то кинетическая энергия фотоэлектронов равна нулю, и формула (1) примет вид:
, соответствующей красной границе фотоэффекта, то кинетическая энергия фотоэлектронов равна нулю, и формула (1) примет вид: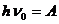 , (4)
, (4)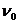 -красная граница фотоэффекта, т.е. максимальная длина волны, при которой ещё возможен фотоэффект.
-красная граница фотоэффекта, т.е. максимальная длина волны, при которой ещё возможен фотоэффект.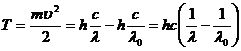 .
.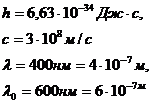
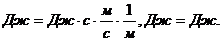
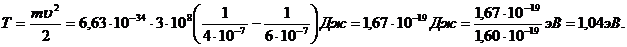
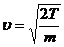 . (6)
. (6)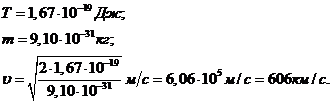
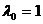 мкм. Вычислить энергетическую светимость
мкм. Вычислить энергетическую светимость 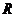 тела при этой температуре и энергию
тела при этой температуре и энергию 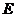 , излучаемую с площади
, излучаемую с площади 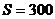 см
см 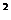 поверхности тела за время
поверхности тела за время 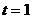 мин. Определить также массу, соответствующую этой энергии.
мин. Определить также массу, соответствующую этой энергии.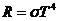 (1)
(1)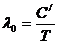 ,
,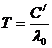 , (2)
, (2)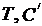 - постоянная Вина.
- постоянная Вина.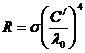 . (3)
. (3)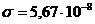 Вт/ (
Вт/ ( 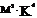 ),
),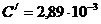 м·К,
м·К,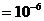 м.
м.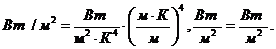
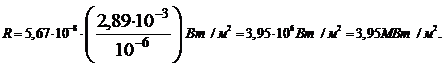
 поверхности тела за 1 мин, определим по формуле:
поверхности тела за 1 мин, определим по формуле: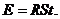 (4)
(4)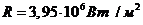 ,
,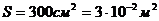 ,
,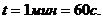
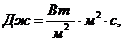
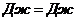
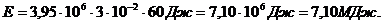
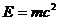 , (5)
, (5)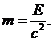 (6)
(6)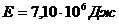 ,
,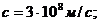
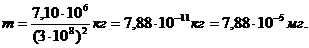
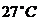 ,если температура окружающей среды
,если температура окружающей среды 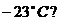 Считать, что тепло теряется только вследствие излучения. Поглощательная способность свинца равна 0,6.
Считать, что тепло теряется только вследствие излучения. Поглощательная способность свинца равна 0,6. (
( 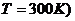 ;
; 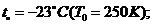
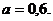
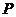
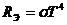 ,
,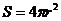 в единицу времени, равную тепловому потоку, выразим
в единицу времени, равную тепловому потоку, выразим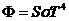 .
.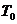 , то шар одновременно и поглощает тепло. Результирующий поток излучения будет равен:
, то шар одновременно и поглощает тепло. Результирующий поток излучения будет равен: 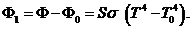
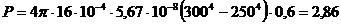 (Вт).
(Вт).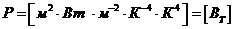
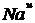 массой 2мг распадается за 10ч и за 0,01с?
массой 2мг распадается за 10ч и за 0,01с?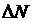 атомов, распавшихся за некоторый промежуток времени
атомов, распавшихся за некоторый промежуток времени 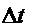 , можно выразить равенством
, можно выразить равенством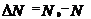
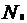 - начальное число атомов (при t = 0);
- начальное число атомов (при t = 0);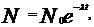
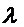 - постоянная радиоактивного распада.
- постоянная радиоактивного распада.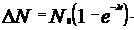
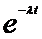
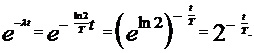
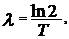 где T- период полураспада.
где T- период полураспада.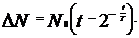
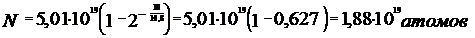 .
.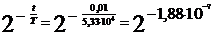
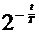 .
. 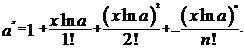

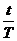 членами разложения, содержащими вторую и более высокие степени числа
членами разложения, содержащими вторую и более высокие степени числа