
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ И ТЕРМОДИНАМИКИ
Идеальные газы подчиняются уравнению состояния Менделеева-Клапейрона: pV= где р – давление газа; V – его объём; Т – термодинамическая температура; m – масса газа; М - молярная масса газа; R=8,31441 Дж/(моль·К) – газовая постоянная; отношение n= m/μ даёт количество газа. По закону Дальтона давление смеси газов равно сумме их парциальных давлений, т.е. тех давлений, которые имел бы каждый из газов в отдельности, если бы он при данной температуре один заполнял весь объём. P=P1+P2+…..+Pn. Основное уравнение кинетической теории газов имеет вид: Р= где п – число молекул в единице объёма; W0 – средняя кинетическая энергия поступательного движения одной молекулы; m0 – масса молекулы;
Эти величины определяются следующими формулами: число молекул в единице объёма: n=P/kT, где k=R/NA= 1.3800662·10-23Дж/к – постоянная Больцмана; NA=6,022045·1023моль-1 – постоянная Авогадро. Средняя кинетическая энергия поступательного движения одной молекулы: W0=3/2 kТ. Средняя квадратичная скорость молекул%
Энергия теплового движения молекул (внутренняя энергия) газа: W= где i – число степеней свободы молекул. Связь между молярной С и удельной с теплоёмкостями следует из их определения:
Молярная теплоёмкость газа при постоянном объёме: СV= Молярная масса при постоянном давлении: CP=CV+R. Средняя длина свободного пробега молекул газа: λ= где z – среднее число столкновений каждой молекулы с остальными в единицу времени; σ - эффективный диаметр молекулы; n – число молекул в единице объёма (концентрация молекул).  Общее число столкновений всех молекул в единице объёма за единицу времени: Z=zn/2. Масса, перенесенная за время Δt при диффузии: m= -D где Δρ/Δx – градиент плотности в направлении, перпендикулярном к площадке ΔS; D= ( Импульс, перенесённый газом за время Δt, определяет силу внутреннего трения Fтр в газе: Fтр=-η где Δu/Δx – градиент скорости течения газа в направлении, перпендикулярном к площадке ΔS; η= Количество теплоты, перенесённой за время Δt вследствие теплопроводности, определяется формулой: Q=-K где ΔT/Δx – градиент температуры в направлении, перпендикулярном к площадке ΔS, K= Первое начало термодинамики может быть записано в виде: dQ=dU+dA, где dQ – количество теплоты, полученное газом; dU – изменение внутренней энергии газа; dA=pdV – работа, совершаемая газом при изменение его объёма. Изменение внутренней энергии газа: dU = где dT – изменение температуры. Полная работа, совершаемая при изменении объёма газа:
Работа, совершаемая при изотермическом изменении объёма газа:
Давление газа и его объём связаны при адиабатическом процессе уравнением Пуассона: pVg=const, т.е. где показатель адиабаты g=ср/сv. Уравнение Пуассона может быть записано ещё в таком виде: TVg-1=const, т.е. или Работа, совершаемая при адиабатическом изменении объёма газа, может быть найдена по формуле: где p1 и V1 – давление и объём газа при температуре Т1. Уравнение политропического процесса имеет вид: pVn=const или p1 где n – показатель политропы (1<n<g) Коэффициент полезного действия (кпд) тепловой машины: η= где Q1 – количество теплоты, полученное рабочим теплом от нагревателя; Q2 – количество теплоты, отданное холодильнику. Для идеального цикла Карно: ηmax= где Т1 и Т2 – термодинамические температуры нагревателя и холодильника. Разность энтропии SB-SA двух состояний В и А определяется формулой: SB-SA= ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР №1. Определить число N молекул, содержащихся в объёме V=1мм3 воды, и массу m1 молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекулы.
РЕШЕНИЕ. Число N молекул, содержащихся в некоторой системе массой m, равно произведению постоянной Авогадро NА на количество вещества ν: N=ν NА . (1) Так как ν=m/M, где М – молярная масса, то Выразив в этой формуле массу как произведение плотности на объём V, получим: N=ρV NА/M. Произведём вычисления, учитывая, что M=18·10-3кг/моль: N= Массу m1 одной молекулы можно найти по формуле: m1=M/ NА. (2) Подставив в (2) значения М и NА, найдём массу молекулы воды:
Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объём (кубическая ячейка) V1=d3, где d – диаметр молекулы. Отсюда d= Объём V1 найдём, разделив молярный объём V на число молекул в моле, т.е. на NА: V1= Vμ / NА . (4) Подставив выражение (4) и (3)
где Vμ=М/ρ. Тогда
Проверим, даст ли правая часть выражения (5) единицу длины:
Произведём вычисления:
ПРИМЕР №2. В баллоне объёмом V=10л находится гелий под давлением Р1=1МПа и при температуре Т1=300К. После того, как из баллона было взято m=10г гелия, температура в баллоне понизилась до температуры Т2=290К. Определить давление Р2 гелия, оставшегося в баллоне.
РЕШЕНИЕ. Для решения задачи воспользуемся уравнением Менделеева − Клапейрона, применив его к конечному состоянию газа: P2V= где m2 – масса гелия в баллоне в конечном состоянии; М – молярная масса гелия; R – молярная газовая постоянная. Из уравнения (1) выразим искомое давление: Массу m2 гелия выразим через массу m1, соответствующую начальному состоянию, и массу m гелия, взятого из баллона: m2= m1- m . (3) Массу m1 гелия найдём также из уравнения Менделеева−Клапейрона, применив его к начальному состоянию:
Подставив выражение массы m1 в (3), а затем выражение m2 в (2), найдём
Проверим, даст ли формула (5) единицу давления. Для этого в её правую часть вместо символов величин подставим их единицы. В правой части формулы два слагаемых. Очевидно, что первое из них даст единицу давления, т.к. состоит из двух множителей, первый из которых (Т2/Т1) − безразмерный, а второй – давление. Проверим второе слагаемое: Паскаль является единицей давления. Произведём вычисления по формуле (5), учитывая, что М=4·10-3кг/моль.
ПРИМЕР №3. Баллон содержит m1=80г кислорода и m2=320г аргона. Давление смеси Р=1МПа, температура Т=300К. Принимая данные газы за идеальные, определить объём баллона.
РЕШЕНИЕ. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева−Клапейрона парциальные давления Р1 кислорода и Р2 аргона выражаются формулами:
Следовательно, по закону Дальтона давление смеси газов Р=Р1+Р2, или
Откуда объём баллона Произведём вычисления, учитывая, что М1=32·10-3кг/моль, М2=40·10-3кг/моль:
ПРИМЕР №4. Найти среднюю кинетическую энергию
РЕШЕНИЕ. На каждую степень свободы молекул газа приходится одинаковая средняя энергия Кинетическая энергия вращательного движения всех молекул газа Ек= Число всех молекул газа N=NАn , (3) где NА – постоянная Авогадро; n - количество вещества. Если учесть, что количество вещества n =т/М, где т – масса газа; М – молярная масса газа, то формула (3) примет вид: N=NАт/М. Подставив выражение N в формулу (2), получаем:
Произведём вычисления, учитывая, что для кислорода М=32·10-3кг/моль: Евращ=kТ=1,38·10-23·350Дж=4,83·10-21Дж Ек=6,02·1023·
ПРИМЕР №5. Вычислить удельные теплоёмкости при постоянном объёме СV и при постоянном давлении Ср неона и водорода, принимая эти газы за идеальные. РЕШЕНИЕ. Удельные теплоёмкости идеальных газов выражаются формулами:
где i – число степеней молекулы газа; М – молярная масса. Для неона (одноатомный газ) i =3 и М=20·10-3кг/моль. Произведём вычисления: Сv= Ср=
Для водорода (двухатомный газ) i =5 и М=2·10-3кг/моль. Тогда Сv= Ср=
ПРИМЕР №6. Вычислить удельные теплоёмкости Сv и Ср смеси неона и водорода, если массовые доли неона и водорода составляют ω1=80% и ω1=20% . Значения удельных теплоёмкостей газов взять из предыдущего примера. РЕШЕНИЕ. Удельную теплоёмкость Сv смеси при постоянном объёме найдём следующим образом. Теплоту, необходимую для нагревания смеси на ΔТ, выразим двумя способами: Q=Cv(m1+m2)ΔT (1) Q=(Cv,1m1+Cv,2m2)ΔT , (2) где Cv,1 – удельная теплоёмкость неона; Cv,2 - удельная теплоёмкость водорода. Приравняв правые части (2) и (1) и разделив обе части полученного равенства на ΔТ, получим : Cv(m1+m2)=Cv,1m1+Cv,2m2, откуда
Сv=Cv,1ω1+ Cv,2ω2, где
Рассуждая так же, получим формулу для вычисления удельной теплоёмкости смеси при постоянном давлении: Ср=Ср,1· ω1+Ср,2· ω2. Произведём вычисления: Сv=(6,24·102·0,8+1,04·104·0,2)Дж/(кг·К)=2,58кДж/(кг·К); Ср=(1,04·103·0,8+1,46·104·0,2)Дж/(кг·К)=3,75кДж/(кг·К).
ПРИМЕР №7. Кислород массой т=2кг занимает объём V1=1м3 и находится под давлением р1=0,2Мпа. Газ был нагрет сначала при постоянном давлении до объёма V2=3м3, а затем при постоянном объёме до давления р3=0,5Мпа. Найти изменение ΔU внутренней энергии газа, совершённую им работу А и теплоту Q, переданную газу. Построить график процесса.
РЕШЕНИЕ. Изменение внутренней энергии газа: ΔU=CvmΔT= где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i=5); ΔТ=Т3-Т1 − разность температур газа в конечном (третьем) и начальном состояниях. Начальную и конечную температуру газа найдём из уравнения Менделеева − Клапейрона: pV= Работа расширения газа при постоянном давлении выражается формулой:
Работа газа, нагреваемого при постоянном объёме, равна нулю, т.е. А2=0. Следовательно, полная работа, совершаемая газом, А=А1+А2=А1. Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии ΔU и работе А: Q=ΔU+ А. Произведём вычисления, учтя, что для кислорода М=32·10 -3кг/моль.
Т3= А1= ΔU=
ПРИМЕР №8. В цилиндре под поршнем находится водород массой т=0,02кг при температуре Т1=300К. Водород сначала расширился адиабатно, увеличив свой объём в n1=5раз, а затем был сжат изотермически, причём объём газа уменьшился в n2=5раз. Найти температуру в конце адиабатного расширения и работу, совершенную газом при этих процессах. Изобразить процесс графически.
РЕШЕНИЕ. Температуры и объёмы газа, совершающего адиабатный процесс связаны между собой соотношениями:
где g – отношение теплоёмкостей газа при постоянном давлении и постоянном объёме, n1=V2/V1. Отсюда получаем следующее выражение для конечной температуры: Т2= Работа А1 газа при адиабатном расширении может быть определена по формуле:
где Сv – молярная теплоёмкость газа при постоянном объёме. Работа А2 газа при изотермическом процессе может быть выражена в виде:
где n2=V2/V3. Произведём вычисления, учтя, что для водорода как двухатомного газа g=1,4; i=5 и М=2·10-3кг/моль:
Так как 50,4=1,91 (находим логарифмированием), то Т2=300/1,91К=157К А1= А2=0,02/0,02·8,31·157ln1/5Дж = -21кДж Знак “минус” показывает, что при сжатии работа совершается над газом внешними силами. График процесса приведён на рисунке.
ПРИМЕР №9. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика Т1=500К. Определить термический кпд η цикла и температуру Т2 теплоприёмника тепловой машины, если за счёт каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу А=350Дж.
РЕШЕНИЕ. Термический кпд тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический кпд выражается формулой η=А/Q1, А=350Дж, Q1=1кДж=103Дж, η=350/1000=0,35. кпд тепловой машины, работающей по обратимому циклу Карно, определяется температурой теплоотдатчика Т1 и теплоприёмникаТ2: η= ηТ1=Т1-Т2; Т2= Т1-ηТ1=Т1(1-η); Т2=500(1-0,35)=325К. ПРИМЕР №10. Два килограмма льда, находящегося при температуре -13ºС, нагрели и расплавили при 0ºС. Определить изменение энтропии. Дано: Найти: Решение. Изменение энтропии
Где Общее изменение энтропии равно сумме Разделим этот процесс на два этапа. На первом - происходит нагревание льда от начальной температуры Так как На втором этапе имеет место плавления льда. В этом случае где Общее изменение энтропии
Проводим вычисления в единицах СИ.
Наименование искомой величины:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 638. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
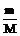 RT,
RT, ,
, - средняя квадратичная скорость молекулы.
- средняя квадратичная скорость молекулы. .
. RT,
RT, .
. R.
R. ,
, – средняя арифметическая скорость;
– средняя арифметическая скорость; ΔSΔt,
ΔSΔt, − коэффициент диффузии
− коэффициент диффузии – средняя арифметическая скорость,
– средняя арифметическая скорость,  - средняя длина свободного пробега молекул).
- средняя длина свободного пробега молекул). ΔS,
ΔS,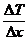 ΔSΔt,
ΔSΔt,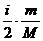 RdT,
RdT,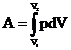 .
. .
. ,
,
 =const, т.е.
=const, т.е.  .
. ,
, =p2
=p2  ,
, ,
, ,
, .
. .
. 6,02*1023 молекул=3,34·1019молекул.
6,02*1023 молекул=3,34·1019молекул. .
. . (3)
. (3) , (5)
, (5) .
. .
. .
. RT2, (1)
RT2, (1)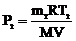 . (2)
. (2) . (4)
. (4) или
или  . (5)
. (5) .
.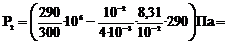 3,64·105Па=0,364МПа.
3,64·105Па=0,364МПа.
 .
. .
. .
. 0,0262м3=26,2л.
0,0262м3=26,2л. вращ вращательного движения одной молекулы кислорода при температуре Т=350К, а также кинетическую энергию Ек вращательного движения всех молекул кислорода массой т=4г.
вращ вращательного движения одной молекулы кислорода при температуре Т=350К, а также кинетическую энергию Ек вращательного движения всех молекул кислорода массой т=4г. 1=
1=  kТ, где k – постоянная Больцмана, Т – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствует две степени свободы, то средняя энергия вращательного движения молекулы кислорода
kТ, где k – постоянная Больцмана, Т – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствует две степени свободы, то средняя энергия вращательного движения молекулы кислорода . (4)
. (4) ·4,83·10-21Дж=364Дж.
·4,83·10-21Дж=364Дж. (1)
(1) , (2)
, (2) Дж/(кг·К)=6,24·102Дж/(кг·К);
Дж/(кг·К)=6,24·102Дж/(кг·К); Дж/(кг·К)=10,4·102Дж/(кг·К).
Дж/(кг·К)=10,4·102Дж/(кг·К). Дж/(кг·К)=1,04·102Дж/(кг·К);
Дж/(кг·К)=1,04·102Дж/(кг·К); Дж/(кг·К)=1,46·102Дж/(кг·К).
Дж/(кг·К)=1,46·102Дж/(кг·К). (3), или
(3), или  и
и 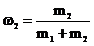 .
. mΔT,
mΔT, .
. .
. Т1=
Т1=  К=385К, Т2=
К=385К, Т2=  К=385К,
К=385К, К=385К,
К=385К, Дж=0,4·106Дж, А=А1=0,4·106Дж,
Дж=0,4·106Дж, А=А1=0,4·106Дж, Дж=3,24·106Дж, Q=(3,24+0,4)·106Дж=3,64·106Дж.
Дж=3,24·106Дж, Q=(3,24+0,4)·106Дж=3,64·106Дж. или
или  ,
, .
.
 или
или  ,
, .
.
 (300-157)Дж = 29,8кДж
(300-157)Дж = 29,8кДж ;
; 

 ,
, - количество тепла, сообщенное телу;
- количество тепла, сообщенное телу; - термодинамическая температура тела;
- термодинамическая температура тела; и
и 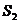 - соответственно значения энтропии в начальном и конечном состояниях системы.
- соответственно значения энтропии в начальном и конечном состояниях системы. , где
, где  -изменение энтропии, происходящее на отдельных этапах процесса,
-изменение энтропии, происходящее на отдельных этапах процесса,  .
. до температуры плавления льда
до температуры плавления льда  и
и  .
. , то
, то  , где
, где 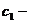 удельная теплоёмкость льда .
удельная теплоёмкость льда . . Тогда
. Тогда  ,
, температура плавления льда;
температура плавления льда;  удельная теплота плавления.
удельная теплота плавления. .
. .
. .
.