
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫОсновные формулы Связь магнитной индукции В с напряженностью Н магнитного поля:
где μ – магнитная проницаемость изотропной среды; μ0 – магнитная постоянная. В вакууме μ=1, и тогда магнитная индукция в вакууме:
Закон Био-Савара-Лапласа:
где dB – магнитная индукция поля, создаваемого элементом проводника длиной dl с током I; r – радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; α – угол между радиус-вектором и направлением тока в элементе проводника. Магнитная индукция в центре кругового тока:
где R – радиус кругового тока. Магнитная индукция на оси кругового тока:
где h – расстояние от центра до точки, в которой определяется магнитная индукция. Магнитная индукция поля прямого тока: B=μμ0I/2πr0, где r0 – расстояние от оси проводника до точки, в которой определяется магнитная индукция. Магнитная индукция поля, создаваемого отрезком провода с током (рис. 12а):
Обозначения ясны из рисунка. Направление вектора магнитной индукции При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рис. 12б): -cosα2 = cosα1= cosα, тогда
Магнитная индукция поля соленоида: В=μμ0nI, где п – отношение числа витков соленоида к его длине. Сила, действующая на проводник с током в магнитном поле (закон Ампера)
где l – длина проводника; α – угол между направлением тока в проводнике и вектором магнитной индукции В. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородное и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности: 
Сила взаимодействия параллельных проводников с током:
где d – расстояние между проводниками. Магнитный момент плоского контура с током:
где I – сила тока, протекающего по контуру; S – площадь контура. Механический (вращательный) момент, действующий на контур с током, помещённый в однородное магнитное поле:
где α – угол между векторами Потенциальная энергия (механическая)* контура с током в магнитном поле: Пмех=- Отношение магнитного момента Pm к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите:
где q – заряд частицы; т – масса частицы. Сила Лоренца:
где u – скорость заряженной частицы; α – угол между векторами Магнитный поток: а) в случае однородного магнитного поля и плоской поверхности: Ф=ВScosα или Ф=Вn·S, где S – площадь контура; α – угол между нормалью к плоскости контура и вектором магнитной индукции; b) в случае неоднородного поля и произвольной поверхности
(интегрирование ведётся по всей поверхности). Потокосцепление (полный поток): Ψ=NФ. Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков. Работа по перемещению замкнутого контура в магнитном поле: А=IΔФ. Э.Д.С. индукции: Разность потенциалов на концах проводника, движущегося со скоростью u в магнитном поле: U=Blusinα, где l – длина проводника; α – угол между векторами Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:
где R – сопротивление контура.
Э.Д.С. самоиндукции:
Индуктивность соленоида: L=μμ0n2V. где n – отношение числа витков соленоида к его длине; V – объём соленоида. Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L: а) где εi – Э.Д.С. источника тока; t – время, прошедшее после замыкания цепи; b) где I0 – сила тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи. Энергия магнитного поля:
Объёмная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объёму): ω=BH/2, или где В – магнитная индукция; Н – напряженность магнитного поля. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР №1. Два параллельных бесконечно длинных провода Д и С, по которым текут в одном направлении электрические токи силой I=60A, расположены на расстоянии d=10см друг от друга (рис. 13). Определить магнитную индукцию поля, создаваемого проводниками в точке А, отстоящей от оси одного проводника на расстояние r1=5см, от другого r2=12см.
Модуль вектора
где α - угол между векторами Магнитные индукции В1 и В2 выражаются соответственно через силу тока I и расстояния r1 и r2 от проводов до точки А:
Подставляя выражения В1 и В2 в формулу (1) и вынося
Вычислим cosα. Заметив, что α равен углу ДСА (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем:
где d – расстояние между проводами. Отсюда
Подставим в формулу (2) числовые значения физических величин и произведём вычисления:
РЕШЕНИЕ. Как известно, на контур с током в магнитном поле действует момент сил: M=PmВsinφ, (1) где Pm – магнитный момент контура; В – магнитная индукция; φ – угол между вектором По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (М=0), а значит, φ=0, т.е. вектора Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Т.к. момент сил переменный (зависит от угла поворота φ), то для подсчёта работы применим формулу работы в дифференциальной форме: dA=Mdφ . Подставив сюда выражение М по формуле (1) и учтя, что Pm =IS=Ia2, где I – сила тока в контуре; S=a2 – площадь контура, получим: dA=IВa2sinφ·dφ . Взяв интеграл от этого выражения, найдём работу при повороте на конечный угол:
1. Работа при повороте на угол φ1=900.
Выразим числовые значения величин в единицах СИ: I=100А; В=1Тл; а=10см=0,1м и подставим в формулу (3): А1=100·1·(0,1)2Дж=1Дж. 2. Работа при повороте на угол φ2=30. В случае, учитывая, что угол φ2 мал, заменим в выражении (2) sinφ≈φ:
Выразим угол φ2=30 в радианах. После подстановки числовых значений величин в (4) найдём: А2=½·100·1·(0,1)2·(0,0523)2Дж=1,37·10-3Дж=1,37мДж. Отметим, что задача могла быть решена и другим способом. Известно, что работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур: А=I(Ф1-Ф2), где Ф1 – магнитный поток, пронизывающий контур до перемещения; Ф2 – то же, после перемещения. В случае φ1=900 Ф1=BS; Ф2=0 . Следовательно, А=IBS=Iba2, что совпадает с полученным выше результатом (3).
ПРИМЕР №3. Электрон, пройдя ускоряющую разность потенциалов U=400В, попал в однородное магнитное поле напряженностью Н=10А/м. Определить радиус R кривизны траектории и частоту обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.
РЕШЕНИЕ. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца Fл (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение: Fл=man, или euB·sinα= где e – заряд электрона; u – скорость электрона; B – магнитная индукция; m – масса электрона; R – радиус кривизны траектории; α - угол между направлением вектора скорости u и вектором B (в данном случае Из формулы (1) найдём:
Входящий в равенство (2) импульс mu может быть выражен через кинетическую энергию Т электрона:
Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством T=eU. Подставив это выражение T в формулу (3), получим
Магнитная индукция В может быть выражена через напряженность магнитного поля в вакууме соотношением В=µ0Н, где µ0 – магнитная постоянная. Подставив найденные выражения В и mu в формулу (2), определим
Выразим все величины, входящие в формулу (4), в единицах СИ: m=9,11·10-31кг, е=1,60·10-19Кл, U=400В, µ0=4π·10-7Гн/м, Н=10А/м. Подставим эти значения в формулу (4) и произведём вычисления: Для определения частоты обращения п воспользуемся формулой, связывающей частоту со скоростью и радиусом:
Подставим в формулу (5) выражение (2) для радиуса кривизны, получим
Все величины, входящие в эту формулу, ранее были выражены в единицах СИ. Подставим их и произведём вычисления:
РЕШЕНИЕ. Мгновенное значение Э.Д.С. индукции εi определяется основным уравнением электромагнитной индукции Фарадея – Максвелла.
где ψ – потокосцепление. Потокосцепление ψ связано с магнитным потоком Ф и числом N витков, прилегающих друг к другу соотношением Ψ=NФ. Подставляя выражение для ψ в формулу (1), получим:
При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону: Ф=ВScosα t, где В – магнитная индукция, S – площадь рамки, ω – круговая (или циклическая) частота. Подставив в формулу (2) выражение Ф и продифференцировав по времени, найдем мгновенное значение Э.Д.С. индукции: εi=NBSw sinω t. (3) Круговая частота ω связана с частотой вращения п соотношением 2πп. Подставляя значение ω в формулу (3), получим: εi=2πnNBSsinω t . Выразим физические величины, входящие в эту формулу, в единицах СИ: n=10с-1; N=103; S=1,5·10-2м2; В = 0,1 Тл; ωt=300=π/6, подставив их в формулу (4), произведём вычисления: εi=2·3,14·10·103·0,1·1,5·10-2·0,5В=47,1В.
ПРИМЕР №5. На железный стержень длиной 50см и сечением 2см намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию магнитного поля в сердечнике соленоида, если сила тока в обмотке 0,5А.
РЕШЕНИЕ. Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течёт ток I, выражается формулой: W= Индуктивность соленоида зависит от числа витков на единицу длины п, от объёма сердечника V и от магнитной проницаемости µ сердечника, т.е. L=µµ0n2V , (2) где µ0 – магнитная постоянная. Магнитную проницаемость можно выразить следующей формулой:
где В – индукция магнитного поля, Н – напряжённость. Подставив в формулу (1) выражения индуктивности L и магнитной проницаемости, получим:
Выразим в этой формуле объём сердечника через его длину и сечение S:
Напряжённость магнитного поля может быть найдена по формуле: Н=пI. Подставив данные в единицах СИ (п=2·10 витков/м, I=0,5А), получим: Н=2·103·0,5А/м=103А/м.
Выразим теперь все данные, входящие в формулу (4), в единицах СИ: В=1,3Тл n=2·103м-1 S=2·10-4м2 Н=103 А/м I=0,5А l=0,5м Подставим эти значения в формулу (4) и произведём вычисления: ПРИМЕР №6. В колебательном контуре, состоящем из индуктивности и ёмкости, максимальный ток в катушке 1А, а максимальное напряжение на конденсаторе 1000В. В момент времени 1,57·10-6с, считая от напряжения, равного нулю, энергия в катушке становится равной энергии в конденсаторе. Вычислить период колебаний контура, энергию контура. (Омическое сопротивление считать пренебрежимо малым). Дано: I0=1А; U=1000В; t=1,57·10-6с; Wэ = Wм . РЕШЕНИЕ. Находим период колебаний контура. По условию в заданный момент энергия магнитного поля равна энергии электрического поля в конденсаторе. Сумма этих энергий определяет полную энергию W контура:
где L – индуктивность контура; I – сила тока в контуре; С – ёмкость конденсатора; U – напряжение на пластинах. Полная энергия контура, выраженная через максимальное напряжение:
Из (1), (2) определим, что Используем уравнение гармонического колебания напряжения (отсчёт ведём от напряжения, равного нулю):
где U0 – амплитуда напряжения (максимальное напряжение); Т – период колебаний; t – время колебания. С учётом (3) получим Вычислим теперь полную (максимальную) энергию контура. Она равна максимальной энергии электрического поля конденсатора (энергия магнитного поля при этом равна нулю) или максимальной энергии магнитного поля (энергия электрического поля равна нулю):
где I0 – максимальный ток в катушке. Используя формулу Томсона
Перемножая (4) и (5) и извлекая корень, определим:
и с учётом (6) получим:
Вычисляем полную энергию: |
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 902. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 =μμ0
=μμ0  ,
, или
или  ,
,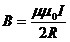 ,
, ,
,
 .
. обозначено точкой – это значит, что
обозначено точкой – это значит, что  .
. или F=IВl·sinα,
или F=IВl·sinα, .
. ,
,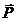 m=
m=  IS,
IS, =[
=[  m·
m·  ,
, =q[
=q[  ·
· 
 .
. или
или  ,
, .
. .
. (при замыкании цепи),
(при замыкании цепи), (при размыкании цепи),
(при размыкании цепи), .
. , или
, или 
 РЕШЕНИЕ. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций В1 и В2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
РЕШЕНИЕ. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций В1 и В2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: , (1)
, (1) ;
;  .
. за знак корня, получаем:
за знак корня, получаем:  . (2)
. (2) ,
, ,
,  .
. =3,08·10-4Тл.
=3,08·10-4Тл. ПРИМЕР №2. Плоский квадратный контур со стороной а=10см, по которому течёт ток I=100А, свободно установился в однородном магнитном поле В=1Тл (рис. 14). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) φ1=900; φ2=30. При повороте контура сила тока в нем поддерживается неизменной.
ПРИМЕР №2. Плоский квадратный контур со стороной а=10см, по которому течёт ток I=100А, свободно установился в однородном магнитном поле В=1Тл (рис. 14). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) φ1=900; φ2=30. При повороте контура сила тока в нем поддерживается неизменной.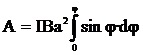 . (2)
. (2) . (3)
. (3) . (4)
. (4) , (1)
, (1) . (2)
. (2) . (3)
. (3)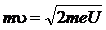 .
. . (4)
. (4) =5,37·10-2м=5,37см
=5,37·10-2м=5,37см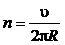 . (5)
. (5) или
или  .
. .
. ПРИМЕР №4. В однородном магнитном поле индукцией В=0,1Тл равномерно с частотой п=10об/с вращается рамка, содержащая N=1000 витков, плотно прилегающих друг к другу (рис. 15). Площадь рамки S=150см2. Определить мгновенное значение Э.Д.С. индукции εi, соответствующее углу поворота рамки в 300.
ПРИМЕР №4. В однородном магнитном поле индукцией В=0,1Тл равномерно с частотой п=10об/с вращается рамка, содержащая N=1000 витков, плотно прилегающих друг к другу (рис. 15). Площадь рамки S=150см2. Определить мгновенное значение Э.Д.С. индукции εi, соответствующее углу поворота рамки в 300. , (1)
, (1) . (2)
. (2) LI2. (1)
LI2. (1) , (3)
, (3) .
. . (4)
. (4)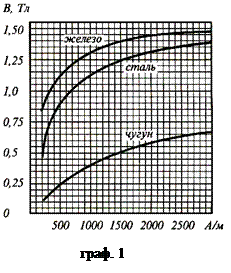 По графику (граф.1) находим, что значению напряжённости магнитного поля 103 А/м в железе соответствует индукция, равная 1,3Тл.
По графику (граф.1) находим, что значению напряжённости магнитного поля 103 А/м в железе соответствует индукция, равная 1,3Тл. Дж=0,065Дж.
Дж=0,065Дж. ;
;  , (1)
, (1) . (2)
. (2) . (3)
. (3) ,
, , отсюда Т=8t. Таким образом, период колебаний в контуре Т=8·1,57·10-6=12,6·10-6(с).
, отсюда Т=8t. Таким образом, период колебаний в контуре Т=8·1,57·10-6=12,6·10-6(с).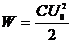 ; (4)
; (4) , (5)
, (5) , получим:
, получим:  . (6)
. (6)
 .
. (Дж).
(Дж).