
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК
Основные формулы Закон Кулона:
где F – сила взаимодействия точечных зарядов q1 и q2; r – расстояние между зарядами; ε – диэлектрическая проницаемость; ε0 – электрическая постоянная. Напряженность электрического поля и потенциал: где П – потенциальная энергия точечного положительного заряда q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удалённого в бесконечность, равна нулю). Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда: F=qE, П=qφ. Напряжённость и потенциал поля, созданного системой точечных зарядов (принцип суперпозиции электрических полей):
где Еi, φi – напряжённость и потенциал в данной точке поля, созданного i-м зарядом. Напряжённость и потенциал поля, созданного точечным зарядом:
где r – расстояние от заряда q до точки, в которой определяются напряжённость и потенциал. Напряжённость и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстояние r от центра сферы: a) Е = 0, b) c) где q – заряд сферы. Линейная плотность заряда: τ =q/l. Поверхностная плотность заряда: σ =q/S. Напряженность и потенциал поля, создаваемого распределёнными зарядами. Если заряд равномерно распределён вдоль линии с линейной плотностью τ , то на линии выделяется малый участок длиной dl с зарядом dq=τdl. Такой заряд можно рассматривать как точечный и применять формулы:
где r – радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряжённость.  Используя принцип суперпозиции электрических полей, находим интегрированием напряжённость Е и потенциал φ поля, создаваемого распределённым зарядом:
Интегрирование ведётся вдоль всей длины l заряженной линии. Напряжённость поля, создаваемого бесконечной прямой, равномерно заряженной линией или бесконечно длинным цилиндром:
где r – расстояние от нити или оси цилиндра до точки, напряжённость поля в которой вычисляется. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью: Е=σ/εε0. Связь потенциала с напряжённостью: a) b) E=(φ1-φ2)/d (в случае однородного поля); c) E=-dφ/dr (в случае поля, обладающего центральной или осевой симметрией). Электрический момент диполя: где q – заряд; l – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами). Работа сил поля по перемещению заряда q из точки поля с потенциалом φ1 в точку с потенциалом φ2: А1-2=q(φ1-φ2). Электроёмкость: С= q/φ или С= q/U, где φ – потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U – разность потенциалов пластин конденсатора. Электроёмкость уединённой проводящей сферы радиусом R: С=4πεε0/R. Электроёмкость плоского конденсатора: С=εε0 S/d, где S – площадь пластины (одной) конденсатора; d – расстояние между пластинами. Электроёмкость батарей конденсаторов: a) b) где n – число конденсаторов в батарее. Энергия заряженного конденсатора: W=qU/2=CU2/2=q2/2C. Сила тока: I=q/t, где q – заряд, прошедший через поперечное сечение проводника за время t. Плотность тока: j=I/S, где S – площадь поперечного сечения проводника. Связь плотности тока со средней скоростью <u> направленного движения заряженных частиц: j=en<u>, где е – заряд частицы; п – концентрация заряженных частиц.
Закон Ома: a) I=(φ1-φ2)/R=U/R (для участка цепи, не содержащего ЭДС), где φ1-φ2 =U – разность потенциалов (напряжение) на концах цепи; R – сопротивление участка; b) где ε – ЭДС источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений); c) I=ε/(R+r) (для замкнутой (полной) цепи), где R – внешнее сопротивление; r – внутреннее сопротивление цепи. Закон Кирхгофа: a) b) где Сопротивление R и проводимость G – проводника: R=ρl/S; G=γS/l, где ρ – удельное сопротивление; γ – удельная проводимость; l – длина проводника; S – площадь поперечного сечения проводника. Сопротивление системы проводников: a) b) где Ri – сопротивление i-го проводника. Работа тока: A=IUt=I2Rt=U2t/R. Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка, не содержащего ЭДС. Мощность тока: P=IU=I2R=U2/R. Закон Джоуля - Ленца: Q=I2Rt. Закон Ома в дифференциальной форме: где γ – удельная проводимость;
Связь удельной проводимости с подвижностью b зараженных частиц (ионов): γ=Qn(b++b-), где Q – заряд иона; n – концентрация ионов; b+ и b- –подвижности положительных и отрицательных ионов.
ПРИМЕР РЕШЕНИЯ ЗАДАЧ
ПРИМЕР №1. Два точечных электрических заряда q1=1нКл и q2=-2нКл находятся в воздухе на расстоянии d=10см друг от друга. Определить напряжённость и потенциал поля, создаваемого этими зарядами в точке А, если расстояние r1=9см и r2=7см.
РЕШЕНИЕ. Общая (результирующая) напряжённость Е в точке А равна сумме напряжённостей двух полей, создаваемых зарядами q1 и q2, т.е.
где На рисунке вектор
Абсолютную величину напряженностей
Выразим числовые значения всех величин в единицах СИ: q1=10-9Кл;q2=-2·10-9Кл;ε=1; r1=9см=0,09м;r2=0,07м; d=0,1м.
Подставив эти числовые значения в формулы (3), (4) и (2), получим:
При вычислении Е2 знак заряда q2 был опущен, так как в данном случае важно знать абсолютное значение напряжённости
Потенциал φ результирующего поля, созданного двумя зарядами q1 и q2, равен алгебраической сумме потенциалов, т.е. φ= φ1+φ2. (5) Потенциал φ1 является положительным, так как поле создано положительным зарядом q1; потенциал φ2 является отрицательным, так как поле создано отрицательным зарядом q2. Потенциал поля, созданного точечным зарядом, определяется по формуле:
Подставив сюда числовые значения величин, получим: Подставив в выражение (5) численные значения потенциалов φ1 и φ2 с учётом их знаков, получим: Φ=100В-257В=-157В. ПРИМЕР №2. Электрон без начальной скорости прошел разность потенциалов U0=10кВ и влетел в пространство между пластинами плоского конденсатора, заряжённого до разности потенциалов U1=100В, по линии АВ, параллельной пластинам. Расстояние d между пластинами равно 2см. Определить расстояние ВС на экране PQ, отстоящем от конденсатора на l2=1м. Длина пластин конденсатора равна 20см.
РЕШЕНИЕ. Движение электрона внутри конденсатора складывается из двух движений: 1) по инерции вдоль линии АВ с постоянной скоростью u0, приобретенной под действием разности потенциалов U0, которую электрон прошел до конденсатора; 2) равномерно ускоренного движения в вертикальном направлении к положительно заряженной пластине под действием постоянной силы поля конденсатора. По выходе из конденсатора электрон будет двигаться равномерно со скоростью u, которую он имел в точке М в момент вылета из конденсатора. Из рисунка видно, что искомое расстояние |ВС|=h1+h2, где h1 – расстояние, на которое сместится электрон в вертикальном направлении во время движения в конденсаторе; h2 – расстояние между точкой Д на экране, в которую электрон попал бы, двигаясь по выходе из конденсатора по направлению начальной скорости u0, и точки С, в которую электрон попадает в действительности. Выразим отдельно h1 и h2. Пользуясь формулой длины пути равномерно ускоренного движения, найдём h1=at2/2, (1) где а – ускорение, полученное электроном под действием поля конденсатора; t – время пролёта электрона внутри конденсатора. По второму закону Ньютона: а=F/m, где F – сила, с которой поле действует на электрон, т – его масса. В свою очередь, F=еЕ=еU1/d, где е – заряд электрона; U1 – разность потенциалов между пластинами конденсатора; d – расстояние между ними. Время полёта электрона внутри конденсатора найдём из формулы пути равномерного движения l1=u0t, откуда t = l1/u0, где l1 – длина конденсатора в направлении полёта электрона. Выражение скорости u0 найдём из условия равенства работы, совершённой полем при перемещении электрона, и приобретённой им кинетической энергии:
Подставляя в формулу (1) последовательно значения a, F, t, и u02 из соответствующих выражений, получим:
Длину отрезка h2 найдём из подобия треугольников ΔМДС и векторного:
где u1 – скорость электрона в вертикальном направлении в точке М; l2 – расстояние от конденсатора до экрана. Скорость u1 найдём по формуле u1=at, которая с учётом выражений для a, F и t примет вид: Подставив выражение u1 в формулу (3), получим:
или, заменив u02 по формуле (3), найдём:
Окончательно для искомого расстояния |ВС| будем иметь: |ВС|=h1+h2= Подставив значение величин U1,U0, d, l1 и l2 в последнее выражение и произведя вычисления, получим |ВС|=5,5см.
ПРИМЕР №3. Конденсатор ёмкостью 3·10-3 Ф был заряжен до разности потенциалов 40В. После отключения от источника тока конденсатор был соединён параллельно с другим незаряженным конденсатором ёмкостью 5·10-3Ф. Какое количество энергии первого конденсатора израсходуется на образование искры в момент присоединения второго конденсатора?
РЕШЕНИЕ. Количество энергии ΔW, израсходованное на образование искры, равно: ΔW=W1 - W2, (1) где W1 – энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W2 – энергия, которую имеет батарея, составленная из первого и второго конденсаторов. Энергия заряженного конденсатора определяется по формуле: W=CU2/2, (2) где С – ёмкость конденсатора или батареи конденсаторов; U – разность потенциалов на обкладках конденсаторов. Выразив в формуле (1) энергии W1 и W2 по формуле (2) и принимая во внимание, что общая ёмкость параллельно соединённых конденсаторов равна сумме ёмкостей отдельных конденсаторов, получим:
где С1 и С2 – ёмкости первого и второго конденсаторов; U1 – разность потенциалов, до которой был заряжен первый конденсатор; U2 – разность потенциалов на зажимах батареи конденсаторов. Учитывая, что заряд после присоединения второго конденсатора остался прежний, выразим разность потенциалов U2 следующим образом:
Подставив это выражение U2 в формулу (3), получим:
После простых преобразований найдём:
В полученное выражение подставим числовые значения и вычислим ΔW: С1=3·10-3Ф С2=5·10-3Ф U1=40В
Дано: ε 1=130В, ε 2=117В, R1=0,5 Ом, R2=0,3 Ом, R3=12 Ом. Найти: I1, I2, I3.
РЕШЕНИЕ. Задача дана для расчёта разветвлённых цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами Кирхгофа. Первый закон сформулирован для узлов, т.е. точек разветвления цепи, в которых сходится больше двух проводников: алгебраическая сумма сил токов, сходящихся в узле, равна нулю.
Второй закон – для замкнутых контуров – гласит: в любом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивление соответствующих участков этого контура равна алгебраической сумме ЭДС в контуре:
Решая совместно составленные по этим законам уравнения, можно определить ту или иную искомую величину (сопротивление внешней цепи или источника, силы токов, ЭДС). Для составления уравнений по указанным законам надо придерживаться следующих правил: 1. Обозначить на схеме буквами узлы и контуры. 2. Произвольно выбрать направления токов (если они не оговорены условием задачи) во всех участках цепи и обозначить их на чертеже стрелками. 3. Учесть направление токов при составлении первого закона. Положительными считать токи, подходящие к узлу, а отрицательными – отходящие от узла. 4. Составить систему уравнений для первого закона Кирхгофа. Число уравнений, составленных по этому закону, должно быть на единицу меньше числа узлов в цепи. 5. Выбрать произвольно направление обхода контуров. Условиться, что ЭДС в уравнении будет положительной, если направление от отрицательного полюса к положительному совпадает с направлением обхода, в противном случае ЭДС следует считать отрицательной. 6. Считать падение напряжения в цепи (IR) положительным, если выбранное ранее направление тока на этом участке (между двумя узлами) совпадает с направлением обхода контура, и отрицательным, если направление тока не совпадает с направлением обхода контура. 7. Первый контур выбирается произвольно. При составлении уравнений следующих контуров надо включать в них контуры, ранее не входившие. 8. Число уравнений, составленных по закону Кирхгофа, определяется следующими условиями: если число контуров в цепи т, а узлов п, то число независимых уравнений, достаточных для решения, будет равно т-п+1 9. Получение в ответе токов с отрицательными знаками означает только то, что было выбрано направление, обратное действительному. Согласно сформулированным выше правилам решаем задачу 4: 1) обозначаем на схеме контуры, узлы и направления токов; 2) установим число т – число ветвей (в данной схеме их три) и число п – число узлов (в схеме их два – в точке В и Н); 3) для составления уравнений по первому закону Кирхгофа, как мы установили, достаточно выбрать один из указанных узлов. Выбираем узел В, в котором сходятся токи от трёх проводников, учитывая направление токов, получим: I1-I2-I3=0; (1) 4) устанавливаем число уравнений, необходимых для решения задач по второму закону Кирхгофа. Это число уравнений равно т-п+1=3-2+1=2. Выбираем контуры ВСДНВ и АВНТА. Устанавливаем обход по контуру ВСДНВ. Учитывая привило знаков при переходе токов внутри источника ЭДС, выбираем обход по часовой стрелке, при котором ЭДС ε1 будет положительной. С учётом выбранного ранее направления токов составляем первое уравнение по второму закону Кирхгофа: -I2R2+I3R3=ε2.(2) Составим уравнение для второго контура. Для этого устанавливаем направление обхода для контура АВНТА. Т.к. в этом контуре два источника тока и ε1 к ε2, обход начинаем от ε1 к ε2 по часовой стрелке. Кроме того, знаки при ЭДС и падении напряжения (IR) устанавливаем в соответствии с ранее записанными правилами: I1R1+I2R2=ε1-ε2. (3) Из уравнения (1) находим: I1=I2+I3. (4) Для определения числовых результатов подставляем в формулу (2) и (3) известные числовые значения сопротивлений и ЭДС: -0,3I2+12I3=117 (5) 0,5I1+0,3I2 =130-117 (6) После сложения (5) и (6) получим: 0,5I1+12I3=130; I1=260-24I3. (7) Подставляя полученную силу тока I1 в (4), находим 260-24·I3=I2+I3. Следовательно, I2=260-25I3 (8) Силу тока I2 (8) используем в выражении (5): 0,3(260-25I3)+12I3=117; 19,5I3=195; I3=10(А). (9) Зная I3 из формулы (7), находим: I1=260-240=20(А). (10) Определяем значение I2 из выражения (4): I2= I1- I3=20-10=10(А).
ПРИМЕР №5. Батарея состоит из пяти последовательно соединённых элементов. ЭДС каждого – 1,4В, внутреннее сопротивление каждого – 0,3 Ом. При каком токе полезная мощность батареи равна 8Вт? Определить наибольшую полезную мощность батареи: Дано: εi=1,4В, ri=0,3 Ом, Pn=8Вт, п=5. Найти: I1, I2, Pn max.
РЕШЕНИЕ. Полезная мощность батареи: Pn=I2R, (1) где R – сопротивление внешней цепи, I – сила тока, которая определяется по закону Ома:
Здесь пεi – ЭДС, а пri – внутреннее сопротивление п последовательно соединённых элементов. Выразим R из (1): R= Pn/ I2 и, подставив это выражение в (2), получим:
I(nri+Pn/ I2)= nεi. (4) Преобразуя выражение (4), получим квадратное уравнение относительно I: nriI2- nεiI+Pn=0. Решая квадратное уравнение, найдём:
Подставляя числовые значения, получим:
Для того, чтобы определить наибольшую полезную мощность батареи, найдём зависимость её от внешнего сопротивления. Подставим в уравнение (1) выражение (2):
Из этой формулы следует, что при постоянных величинах εi и пri мощность является функцией одной переменной – внешнего сопротивления R. Известно, что эта функция имеет максимум, если dPn/dR=0, следовательно, имеем:
Таким образом, задача сводится к отысканию сопротивления внешней цепи. Из решения уравнения (6) следует R=пri . Подставляя найденные значения R в формулу (5), имеем:
Произведя вычисления, найдём: Pn max=5·1,42/4·0,3=8,16(Вт). Ответ: I1=2,66А, I2=2А, Pn max=8,16Вт. ПРИМЕР №6. Вычислить общее сопротивление цепи, если R1=2 Ом, R2=1 Ом, R3=4/3 Ом, R4=3 Ом, R5=5 Ом, R6=2 Ом. Какой ток потечёт через резисторы, если контур подключить точками А и В к источнику напряжения 10В?
R5,6=1 Ом. Сопротивление R4 соединено с эквивалентным сопротивлением R5,6 последовательно: R4,5,6= R5,6+R4=1 Ом+3 Ом=4 Ом. Сопротивление R3 соединено с эквивалентным сопротивлением R4,5,6 параллельно:
Аналогично R2-6= R3-6+R2=1 Ом+1 Ом=2 Ом.
Rобщ=1 Ом. Расчёт токов начинаем с определения тока в неразветвлённой части цепи (Iобщ): Iобщ=U/Rобщ=10B/1 Ом=10A. Сила тока, протекающего через сопротивление R1: I1=U/R1=10B/2 Ом=5A (т.к. U1=U). При параллельном соединении ток в неразветвлённой цепи равен сумме токов в ветвях: Iобщ= I1+ I2; I2= Iобщ - I1=10А-5А=5А. Падение напряжения на R2 определим по закону Ома:
U2=I2R2=5A·1 Ом=5В. Напряжение на резисторе R3: U3=U-U2=10В-5В=5В. Сила тока:
I4= I2-I3 =5А - 15/4А = 5/4А;
U4 =I4R4 = 5/4А·3 Ом = 15/4В; U5=U3-U4 =5В - 15/4В = 5/4В;
I6= I4 -I5 = 5/4А - 5/8А = 5/8А. ЭЛЕКТРОМАГНЕТИЗМ. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 876. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
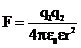 ,
, =
=  /q, φ=П/q,
/q, φ=П/q,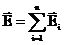 ;
;  ,
,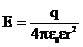 ;
; 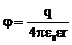 ,
,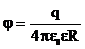 (при R>r),
(при R>r), ,
,  (при r=R),
(при r=R), ,
,  (при r>R),
(при r>R), ,
,  ,
, ,
,  .
. ,
, = -qrad φ,или
= -qrad φ,или  ;
; =|q|·
=|q|·  ,
, (при последовательном соединении);
(при последовательном соединении); (при параллельном соединении);
(при параллельном соединении);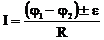 (для участка цепи, содержащего ЭДС),
(для участка цепи, содержащего ЭДС), (первый закон);
(первый закон); (второй закон),
(второй закон), – алгебраическая сумма сил токов, сходящихся в узле;
– алгебраическая сумма сил токов, сходящихся в узле; – алгебраическая сумма произведений сил токов на сопротивления участков контура;
– алгебраическая сумма произведений сил токов на сопротивления участков контура;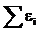 – алгебраическая сумма ЭДС.
– алгебраическая сумма ЭДС.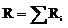 (при последовательном соединении);
(при последовательном соединении); (при параллельном соединении),
(при параллельном соединении), ,
, – плотность тока.
– плотность тока.
 , (1)
, (1)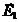 – напряжённость поля заряда
– напряжённость поля заряда – напряжённость поля заряда q2.
– напряжённость поля заряда q2. направлен от заряда q1, так как этот заряд положительный, вектор
направлен от заряда q1, так как этот заряд положительный, вектор  . (2)
. (2) ; (3)
; (3) . (4)
. (4) Ф/м.
Ф/м.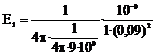 В/м=1,11·103 В/м;
В/м=1,11·103 В/м; В/м=3,68·103 В/м.
В/м=3,68·103 В/м. ;
; В/м =3,58×103 В/м.
В/м =3,58×103 В/м. . (6)
. (6) В =100В;
В =100В; В = - 257В.
В = - 257В.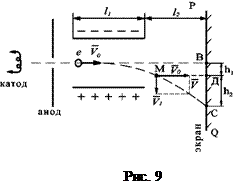
 . Откуда
. Откуда . (2)
. (2)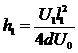 .
. , (3)
, (3) .
.
 .
. .
. , (3)
, (3)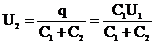 .
. .
. .
. Дж=1,5Дж
Дж=1,5Дж ПРИМЕР №4. Найти токи, протекающие в каждой ветви электрической цепи (рис.10), если ε1=130В, ε2=117В, R1=0,5 Ом, R2=0,3 Ом, R3=12 Ом. Внутреннее сопротивление источников ЭДС не учитывать.
ПРИМЕР №4. Найти токи, протекающие в каждой ветви электрической цепи (рис.10), если ε1=130В, ε2=117В, R1=0,5 Ом, R2=0,3 Ом, R3=12 Ом. Внутреннее сопротивление источников ЭДС не учитывать. .
. .
. . (2)
. (2) ; (3)
; (3)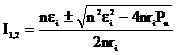 .
. ;
;  .
.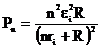 . (5)
. (5) или
или  . (6)
. (6) .
. РЕШЕНИЕ. Данное соединение является смешанным, т.к. в нём присутствуют элементы параллельного и последовательного соединения. Расчёт общего сопротивления начинаем с самого элементарного контура, образованного параллельно соединёнными резисторами R5 и R6.
РЕШЕНИЕ. Данное соединение является смешанным, т.к. в нём присутствуют элементы параллельного и последовательного соединения. Расчёт общего сопротивления начинаем с самого элементарного контура, образованного параллельно соединёнными резисторами R5 и R6.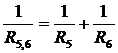 ;
; (Ом-1);
(Ом-1); ;
;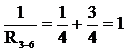 (Ом-1); R3-6=1 Ом.
(Ом-1); R3-6=1 Ом. ;
;  (Ом-1).
(Ом-1).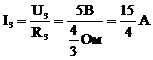 ;
; ;
;