Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Номера задач для контрольной работы по физикеСтр 1 из 9Следующая ⇒ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ ПО ФИЗИКЕ
для студентов инженерных специальностей заочного отделения
Оренбург - 2010 ББК 22.3 С 24 УДК 53
Одобрено и рекомендовано к печати методической комиссией факультета механизации С/Х. Протокол № 2 от 26.02.2010.
Составители: Т.Г. Свиридова С.А. Ишкаева Рецензенты: проф. д.т.н. В.Г. Петько, к.ф-м.н. В.П. Дружинин
Учебное пособие содержит формулы и примеры решения задач по основным разделам физики, контрольные задания, справочные материалы. Книга предназначена для студентов-заочников инженерных специальностей ОГАУ.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ Учебная работа студента-заочника по изучению курса физики складывается из следующих основных элементов: самостоятельного изучения физики по учебным пособиям, решения задач, выполнения контрольных работ, выполнения лабораторных работ и сдачи зачетов и экзаменов.
САМОСТОЯТЕЛЬНАЯ РАБОТА ПО УЧЕБНЫМ ПОСОБИЯМ
Самостоятельная работа по учебным пособиям является главным видом работы студента-заочника. Студентам рекомендуется руководствоваться следующими положениями: 1. Изучать курс физики следует систематически в течение всего учебного процесса. Изучение курса в сжатые сроки перед экзаменом не даст глубоких и прочных знаний по физике. 2. Избрав какое-нибудь учебное пособие в качестве основного по определенной части курса физики, студент должен придерживаться данного пособия при изучении всей части или, по крайней мере, целого его раздела. Замена одного пособия другим в процессе изучения может привести к утрате логической связи между отдельными вопросами. Но если основное пособие не дает полного или ясного ответа на некоторые вопросы программы, необходимо обращаться к другим учебным пособиям.  3. Чтение учебного пособия следует сопровождать составлением конспекта, в котором записываются формулировки законов и формулы, выражающие законы, определения физических величин и единиц измерения этих величин, делаются чертежи и выполняется решение типовых задач. 4. Физика- наука точная, и физические исследования связаны с измерением физических величин. Поэтому при изучении курса физики студент встретится с большим количеством единиц измерения, объединенных в особые системы единиц. Студент должен твердо запомнить, что без основательного знания систем единиц, без умения пользоваться ими при решении физических задач невозможно усвоить курс физики и тем более применять физические знания на практике. При решении задач следует преимущественно пользоваться Международной системой единиц (СИ). 5. Самостоятельную работу по изучению физики студент должен подвергать систематическому самоконтролю. С этой целью после изучения определенного раздела физики следует ставить вопросы, касающиеся формулировок законов, определений физических величин и единиц измерения, и отвечать на эти вопросы.
РЕШЕНИЕ ЗАДАЧ
Систематическое решение задач является необходимым условием успешного курса физики. Решение задач помогает уяснить физический смысл явлений, закрепляет в памяти формулы, прививает навыки практического применения теоретических знаний. При решении задач необходимо выполнить следующее: 1. Указать основные законы и формулы, на которых базируется решение задачи, дать словесную формулировку этих законов, разъяснить буквенные обозначения, употребляемые при написании формул. Если при решении задачи применяется формула, полученная для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то ее следует вывести. 2. Дать чертеж, поясняющий содержание задачи (в тех случаях, когда это возможно); выполнять его надо аккуратно при помощи чертежных принадлежностей. 3. Сопровождать решение задачи краткими, но исчерпывающими пояснениями. 4. Выразить все величины, входящие в условие задачи, в единицах одной системы и выписать их для наглядности столбиком. Как уже указывалось, преимущественно следует пользоваться Международной системой единиц (СИ). 5. Подставить в окончательную формулу, полученную в результате решения задачи в общем виде, числовые значения, выраженные в единицах одной системы. Несоблюдение этого правила приводит к неверному результату. Исключение из этого правила допускается только для тех величин, которые входят в числитель и знаменатель формулы с одинаковыми показателями степени. Такие величины не обязательно выражать в единицах этой системы, в которой ведется решение задачи. Их можно выразить в любых, но только одинаковых единицах. 6. Проверить, дает ли рабочая формула правильную размерность искомой величины. Для этого в рабочую формулу следует подставить размерность всех величин и произвести необходимые действия. Если полученная таким путем размерность не совпадает с размерностью искомой величины, то задача решена неверно. 7. Произвести вычисление величин, подставленных в формулу, руководствуясь правилами приближенных вычислений, записать в ответе числовое значение и сокращенное наименование или размерность единицы измерения искомой величины в той системе, в которой производилось вычисление. Физические задачи весьма разнообразны, и дать единый рецепт их решения невозможно. Однако, как правило, физические задачи следует решать в общем виде, т.е. в буквенных выражениях. При этом способе не производятся вычисления промежуточных величин; числовые значения подставляются только в окончательную (рабочую) формулу, выражающую искомую величину. Умение решать задачи приобретается длительными и систематическими упражнениями. Чтобы научиться решать задачи и подготовиться к выполнению контрольной работы, следует после изучения очередного раздела учебника внимательно разобрать помещенные в настоящем пособии примеры решения типовых задач, а также ряд задач из задачников по физике.
ВЫПОЛНЕНИЕ КОНТРОЛЬНЫХ РАБОТ
Выполнение контрольных работ студентом и рецензирование их преподавателем преследуют две цели: во-первых, осуществление контроля за работой студента; во-вторых, оказание ему помощи в вопросах, которые оказались слабо усвоенными или непонятными студентом. К выполнению контрольных работ по каждому разделу курса физики студент-заочник приступает только после изучения материала, соответствующего данному разделу программы, внимательного ознакомления с примерами решения задач, приведенных в данном пособии по каждому разделу курса.
При выполнении контрольных работ студенту необходимо руководствоваться следующим: 1. Контрольные работы выполняются только по условиям задач данного пособия. Замена какой-либо контрольной другой, взятой из аналогичного пособия, но другого года издания, не допускается. 2. Для замечаний преподавателя на страницах тетради оставляются поля. Каждая следующая задача должна начинаться с новой страницы. Условия задач переписываются полностью без сокращений. 3. Решения задач должны сопровождаться исчерпывающими, но краткими объяснениями, раскрываемых физический смысл употребляемых формул, и выполняться в соответствии с правилами, изложенными в параграфе «Решения задач». 4. В конце контрольной работы необходимо указать, каким учебником или учебным пособием студент пользовался при изучении физики (название учебника, автор, год издания). 5. В случае, если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторная работа представляется вместе с незачтенной работой. 6. Зачтенные контрольные работы предъявляются экзаменатору. Студент должен быть готов дать во время экзамена пояснения по существу решения задач, входящих в его контрольные работы. 7.Выбор задач производится по приведенной ниже таблице следующим образом: в первом столбце таблицы выбирается цифра, соответствующая предпоследней цифре в номере зачетной книжки, в первой строке таблицы выбирается цифра, соответствующая последней цифре в номере зачетной книжки, на пересечении данной строки и столбца находится ячейка с номерами заданий для заданного варианта.
Номера задач для контрольной работы по физике
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
Основные формулы Кинематическое уравнение движения материальной точки (центра масс твёрдого тела) вдоль оси Х: x=f(t), где f(t) − некоторая функция времени. Средняя скорость: Средняя путевая скорость: где ΔS − путь, пройденный точкой за интервал времени Δt. Путь ΔS в отличие от разности координат Δx=x2-x1 не может убывать и принимать отрицательные значения, т.е.ΔS ≥0 . Мгновенная скорость: Среднее ускорение: Мгновенное ускорение: Кинематическое уравнение движения материальной точки по окружности: r=f(t), r=R=const. Угловая скорость: Угловое ускорение: Связь между линейными и угловыми величинами, характеризующими движение точки по окружности: u =ωR, aτ=εR, an = ω2R, где u − линейная скорость; aτ и an − тангенциальное и нормальное ускорения; ω − угловая скорость; ε − угловое ускорение; R − радиус окружности. Полное ускорение: Угол между полным а и нормальным ап ускорениями: α=arccos(an/a).
Кинематические уравнения равномерного движения
Поступательное Вращательное
Кинематические уравнения равнопеременного движения
Поступательное Вращательное
Кинематическое уравнение гармонических колебаний материальной точки: x=Acos(ωt+φ0), где х − смещение; А – амплитуда колебаний; ω − круговая или циклическая частота; φ0 − начальная фаза. Скорость и ускорение материальной точки, совершающей гармонические колебания: u = -Aω sin(ωt+φ0), a= -Aω2cos(ωt+φ0). Сложение гармонических колебаний одного направления и одинаковой частоты: 1. Амплитуда результирующего колебания 2. Начальная фаза результирующего колебания: Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях (x=A1cosωt, y=A2cos(ωt+φ0)): a. y=(A2/A1)x (если разность фаз Δφ=0); b. y=-(A2/A1)x (если разность фаз Δφ=±π); c. Уравнение плоской бегущей волны: y=Acosω(t-x/v), где у – смещение любой из точек среды с координатой х в момент времени t; u – скорость распространения колебаний в среде. Связь разности фаз Δφ колебаний с расстоянием Δx между точками среды, отсчитанным в направлении распространения колебаний: Δφ=(2π/λ)Δx, где λ − длина волны. Импульс материальной точки массой т, движущейся поступательно со скоростью Второй закон Ньютона: d где Силы, рассматриваемые в механике: a) сила упругости: F= –k x, где k – коэффициент упругости (в случае пружины – жёсткость), х – абсолютная деформация; b) сила тяжести: P=mg c) сила гравитационного взаимодействия: где G – гравитационная постоянная; т1 и т2 – массы взаимодействующих тел; r –расстояние между телами (тела рассматриваются как материальные точки). d) сила трения (скольжения): F=fN, где f – коэффициент трения; N – сила нормального давления, Закон сохранения импульса: или для двух тел (i=2): m1 где Кинетическая энергия тела, движущегося поступательно: T=mu2/2, или T=p2/(2m). Потенциальная энергия: a) упругодеформированной пружины: П= где k – жёсткость пружины; х – абсолютная деформация; b) гравитационного взаимодействия: П= -Gm1m2/r, где G – гравитационная постоянная; т1 и т2 – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки); c) тела, находящегося в однородном поле силы тяжести: П=mgh, где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R – радиус Земли). Закон сохранения механической энергии: E=T+П=const. Работа А, совершаемая внешними силами, определяется как мера измерения энергии системы: A=ΔE=E2-E1, A=FScosα, (F=const); A= Мощность средняя: Мощность мгновенная: Связь мощности со скоростью: Коэффициент полезного действия: где
Основное уравнение динамики вращательного движения относительно неподвижной оси z: где Mz – результирующий момент внешних сил относительно оси z; e – угловое ускорение; Jz – момент инерции тела относительно оси z. Момент инерции некоторых тел массой т относительно оси z, проходящий через центр масс: a) стержень длиной l относительно оси, перпендикулярной стержню: Jz=1/12ml2; b) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра): Jz=mR2, где R – радиус обруча (цилиндра); c) диска радиусом R относительно оси, перпендикулярной плоскости диска: Jz=1/2mR2. Момент импульса тела, вращающегося относительно неподвижной оси z:
где ω - угловая скорость тела. Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси: где Кинетическая энергия тела, вращающегося вокруг неподвижной оси z: T=1/2Jzw2 или T= Кинетическая энергия тела, совершающего одновременно поступательное и вращательное движения:
где Работа при вращательном движении тела:
Мощность при вращательном движении тела:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример №1.Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct3, где А=2м, В=1м/с, С=-0,5м/с3. Найти координату х, скорость и ускорение точки в момент времени t=2c. РЕШЕНИЕ. Координату х найдём, поставив в уравнение движения числовые значения коэффициентов А,В и С и времени t: х=(2+1·2-0,5·23)м=0. Мгновенная скорость есть первая производная от координаты по времени: u = Ускорение точки найдём, взяв первую производную от скорости по времени: a = В момент времени t=2c:
a=6·(-0,5)·2м/с2=-6 м/с2. ПРИМЕР №2. Тело вращается вокруг неподвижной оси по закону φ=A+Bt+Ct2, где А=10 рад, В=20 рад/с, С=-2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r=0,1м от оси вращения для момента времени t=4c. РЕШЕНИЕ. Полное ускорение Так как векторы aτ и ап взаимно перпендикулярны, то модуль ускорения:
Тангенциальное и нормальное ускорение точки вращающегося тела выражается формулами: aτ=e r, an=ω 2r, (2) где ω – угловая скорость тела, e–его угловое ускорение. Подставляя выражения aτ и ап в формулу (1), находим:
Угловую скорость ω найдём, взяв первую производную угла поворота по времени: ω=dφ/dt=B+2Ct. В момент времени t=4с угловая скорость ω=[20+2(-2)4]рад/с. Угловое ускорение найдём, взяв первую производную от угловой скорости по времени: ε=dω/dt=2C= -4рад/с2. Подставляя значения ω, ε и r в формулу (2), получаем: а = 0,1 ПРИМЕР №3. Какую мощность развивает двигатель автомобиля массой 1т, если известно, что автомобиль едет с постоянной скоростью 36 км/ч: 1. по горизонтальной дороге, 2. в гору с уклоном 5м на каждые 100м пути, 3. под гору с тем же уклоном. Коэффициент трения равен 0,07.
1) Сила тяжести mg и сила реакции опоры Fупр уравновешивают друг друга. По второму закону Ньютона ma=F-Fтр. Т.к. автомобиль движется с постоянной скоростью а=0 и, следовательно, F=Fтр=μmg. Тогда m=1т=103кг; N=0,07·103·9,8·10=6,9·103Вт=6,9кВт.
2) При движении в гору автомобилю приходится преодолевать силу трения и составляющую силы тяжести F1, параллельную пути: F=Fтр+ F1 , Fтр=μF2= μ mg cosα , F1=mg sinα. Таким образом, сила тяги F=μmgcosα+mgsinα или F=mg(μcosα+sinα). Учитывая, что sinα=h/l=0,05 и cosα= получим F=103·9,8·(0,07+0,05)=1,98кН, N=F
F+ F1=Fтр F=Fтр- F1 Если сила трения меньше F1, то F<0. Это означает, что для осуществления равномерного движения автомобиля под гору необходимо приложить задерживающую (тормозную) силу, направленную вверх вдоль наклонной плоскости.
F1=mgsinα=103·9,8·0,05=490Н Fтр=μmgcosα =0.07·103·9,8·1=686Н F=Fтр- F1=686-490=196Н N=Fu=196·10=1,96кВт ПРИМЕР №4. При выстреле из пружинного пистолета вертикально вверх пуля массой m=20г поднялась на высоту h=5м. Определить k жёсткость пружины пистолета, если она была сжата на х=10см. Массой пружины пренебречь.
РЕШЕНИЕ. Система пуля-Земля (вместе с пистолетом) является замкнутой системой, в которой действуют консервативные силы, – силы упругости и силы тяготения. Поэтому для решения задачи можно применить закон сохранения энергии в механике. Согласно ему, полная механическая энергия Е1 системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии Е2 в конечном состоянии (когда пуля поднялась на высоту h), т.е. Е1 = Е2 или T1+ П1= T2+ П2, (1) где T1 , T2, П1 и П2 – кинетические и потенциальные энергии системы в начальном и конечном состояниях. Т.к. кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид: П1=П2 . (2) Если потенциальную энергию в поле сил тяготения Земли на её поверхности принять равной нулю, то энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины: П1=1/2kх2, а в конечном состоянии – потенциальной энергии пули на высоте h: П2=mgh. Подставив выражения П1и П2 в формулу (2), найдём: 1/2kх2=mgh откуда k=2mgh/x2. (3) Проверим, даст ли полученная формула единицу жёсткости k. Для этого в первую часть формулы (3) вместо величин подставим их единицы:
Убедившись, что полученная единица является единицей жёсткости (1Н/м), подставим в формулу (3) значения величин и произведём вычисления: k=2·0,02·9,81·5/(0,1)2Н/м=196Н/м. ПРИМЕР №5. Шар массой m1, движущийся горизонтально с некоторой скоростью u1, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю в своей кинетической энергии первый шар передал второму? РЕШЕНИЕ.Доля энергии, переданной первым шаром второму, выразится соотношением E= где Т1 – кинетическая энергия первого шара до удара; U2 и Т2 – скорость и кинетическая энергия второго шара после удара. Как видно из формулы (1), для определения E надо найти U2. При ударе абсолютно упругих тел одновременно выполняются законы сохранения импульса и механической энергии. Пользуясь этими законами, найдём: m1u1= m1U1+ m2U2; (2) Решим совместно уравнения (2) и (3): U2= Подставив это выражение в формулу (1) и сократив на u1 и m1, получим: E= Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменять местами.
РЕШЕНИЕ. Воспользуемся основными уравнениями динамики поступательного и вращательного движения. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действуют две силы: сила тяжести m1g и силы упругости (сила натяжения нити) Т1. Спроецируем эти силы на ось х, которую направим вертикально вниз, и напишем уравнение движения (второй закон Ньютона): m1g-T1= -m1a. (1) Уравнение движения для второго груза: m2g-T2= m2a . (2) Под действием двух моментов сил
где e=a/r, Jz=1/2mr2– момент инерции блока (сплошного диска) относительно оси z. Согласно третьему закону Ньютона, (m2g-m2a)r-(m1g+m1a)r=mr2a/(2r). После сокращения на r и перегруппировки членов найдём: а = Отношение масс в правой части формулы (4) есть величина безмерная. Поэтому массы m1, m2 и m можно выразить в граммах, как они даны в условии задачи. Ускорение g надо выразить в единицах СИ. После подстановки получим: а=[(200-100)г/(200+100+80/2)г]·9,81м/с2=2,88м/с2. ПРИМЕР №7.Тело массой РЕШЕНИЕ 1. При равномерном вращении тела уменьшение длины нити создается силой F, направленной вдоль радиуса
где Следовательно, начальный момент импульса где R- радиус окружности, по которой вращается тело. Угловую скорость выразим через линейную: Для начального момента времени по формулам (2) и (3) получим
После укорачивания нити Подставляя в (1) выражения (4) и (5), получаем
После преобразований с учетом того, что
Проверим расчетную формулу (6) :
Выразим числовые значения величин в СИ: Вычислим искомую конечную скорость:
2. Для определения частоты вращения Приравнивая их правые части, получаем Проверим формулу (7):
Вычислим искомую конечную частоту вращения:
ПРИМЕР №8 Диск, катившийся со скоростью Решение. Кинетическая энергия диска равна сумме кинетических энергий поступательного и вращательного движений: Здесь Подставив в (1) выражение для
Выражение (2)можно использовать для записи полной кинетической энергии
Разность кинетических энергии
Подставив данные задачи, вычислим искомую разность энергий:
Знак минус показывает, что произошло уменьшение кинетической энергии диска.
ПРИМЕР №9Материальная точка с массой 0,01кг совершает гармонические колебания с периодом 2с. Полная энергия колеблющейся точки равна РЕШЕНИЕ 1. Запишем уравнение гармонических колебаний в общем виде:
Взяв первую производную смещения
Кинетическая энергия колеблющейся точки:
Полная энергия колеблющейся точки равна максимальному значению кинетической энергии точки:
Отсюда находим следующее выражение для амплитуды колебаний:
Циклическая частота
Подставим это соотношение в предыдущее выражение
и произведем вычисления:
Найдем числовое значение циклической частоты:
2. Запишем уравнение гармонических колебаний для данной точки:
3. Ускорение колеблющейся точки найдем, взяв производную от скорости по времени:
Отсюда максимальное ускорение
Подставив это выражение максимального ускорения в формулу второго закона динамики, найдем максимальную силу, действующую на точку:
Произведем вычисления:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 632. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
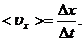
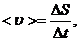
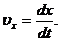
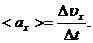
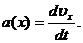
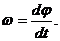
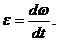
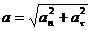 или
или 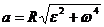 .
.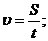
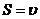
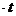
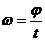 ;
; 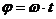
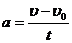
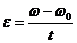
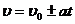
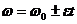
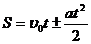
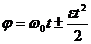

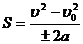
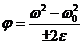
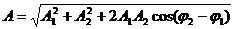 .
.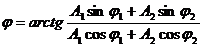 .
.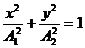 (если разность фаз Δφ=±π/2).
(если разность фаз Δφ=±π/2). :
: 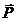 =m
=m  dt,
dt,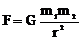 ,
,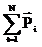 =const
=const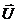 1+ m2
1+ m2 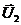 .
.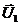 и
и 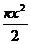 ,
,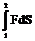 , (F≠const).
, (F≠const).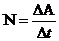
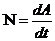
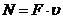
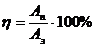 ,
,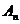 - полезная работа;
- полезная работа;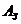 - затраченная работа.
- затраченная работа. z=Jz
z=Jz 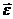 ,
,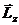 =Jz
=Jz 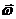 ,
,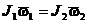 ,
,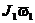 и
и 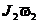 − момент n инерции системы сил и угловые скорости вращения в момент n времени, принятые за начальный и конечный.
− момент n инерции системы сил и угловые скорости вращения в момент n времени, принятые за начальный и конечный.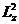 /(2J z).
/(2J z).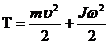 ,
,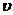 - скорость движения центра масс тела
- скорость движения центра масс тела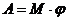 (
( 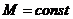 );
);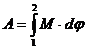 (
( 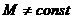 ).
).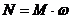 .
.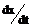 =B+3Ct2.
=B+3Ct2.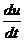 =6Ct.
=6Ct.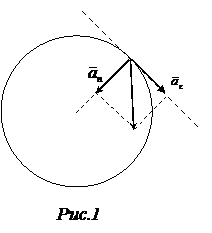 u =(1-3·0,5·22)м/с=-5м/с,
u =(1-3·0,5·22)м/с=-5м/с,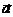 точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения
точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения 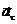 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения 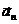 , направленного к центру кривизны траектории (рис.1):
, направленного к центру кривизны траектории (рис.1): 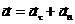
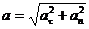 . (1)
. (1)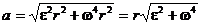 . (3)
. (3)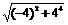 м/с2=1,65м/с2.
м/с2=1,65м/с2.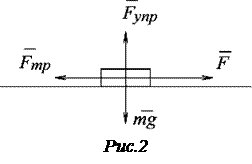 Решение. Мощность, развиваемая двигателем автомобиля, связана со скоростью движения автомобиля соотношением N=Fu, где F – сила тяги, развиваемая двигателем автомобиля; u – скорость движения. Следовательно, решение задачи сводится к определению силы тяги в каждом из трёх случаев.
Решение. Мощность, развиваемая двигателем автомобиля, связана со скоростью движения автомобиля соотношением N=Fu, где F – сила тяги, развиваемая двигателем автомобиля; u – скорость движения. Следовательно, решение задачи сводится к определению силы тяги в каждом из трёх случаев.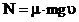
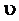 =36км/ч=10м/с; g=9,8м/с2
=36км/ч=10м/с; g=9,8м/с2 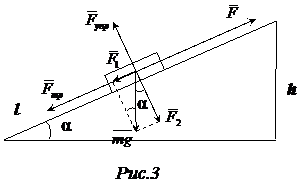
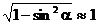 ,
,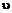 =1,98·103·10=19,8·103=19,8кВт.
=1,98·103·10=19,8·103=19,8кВт.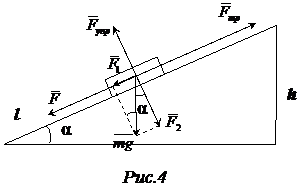 3) При равномерном движении автомобиля под гору сила трения должна уравновешивать силу тяги и составляющую силу тяжести, параллельную пути:
3) При равномерном движении автомобиля под гору сила трения должна уравновешивать силу тяги и составляющую силу тяжести, параллельную пути: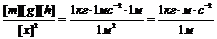 =1Н/м.
=1Н/м.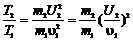 , (1)
, (1)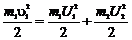 . (3)
. (3)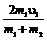 .
.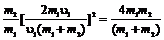 .
.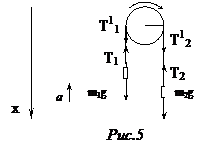 ПРИМЕР №6.Через блок в виде сплошного диска, имеющего массу m=80г (рис.5), перекинута тонкая гибкая нить к концам которой подвешены грузы с массами m1=100г и m2=200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
ПРИМЕР №6.Через блок в виде сплошного диска, имеющего массу m=80г (рис.5), перекинута тонкая гибкая нить к концам которой подвешены грузы с массами m1=100г и m2=200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.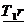 и
и  относительно оси, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения:
относительно оси, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения: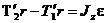 , (3)
, (3)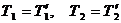 . Воспользуемся этим, подставив в уравнение (3) вместо
. Воспользуемся этим, подставив в уравнение (3) вместо 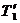 и
и 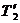 выражения T1 и T2, получив их предварительно из уравнений (1) и (2):
выражения T1 и T2, получив их предварительно из уравнений (1) и (2): 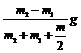 . (4)
. (4)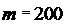
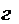 прикреплено к нити и вращается по окружности радиусом
прикреплено к нити и вращается по окружности радиусом 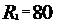
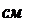 с постоянной линейной скоростью
с постоянной линейной скоростью 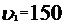
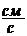 . При вращении нить укорачивается на длину
. При вращении нить укорачивается на длину 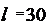
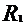 . Плечо этой силы равно нулю; следовательно, момент силы M=FR также равен нулю. Вращение тела, свободного от действия моментов сил, подчиняется закону сохранения момента импульса:
. Плечо этой силы равно нулю; следовательно, момент силы M=FR также равен нулю. Вращение тела, свободного от действия моментов сил, подчиняется закону сохранения момента импульса: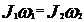 , (1)
, (1)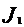 и
и 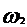 - момент инерции и угловая скорость тела в начальный момент времени;
- момент инерции и угловая скорость тела в начальный момент времени; 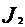 и
и 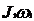 равен моменту импульса
равен моменту импульса 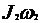 тела после укорачивания нити. Считая, что тело представляет собой материальную точку, определим его момент инерции:
тела после укорачивания нити. Считая, что тело представляет собой материальную точку, определим его момент инерции: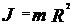 , (2)
, (2)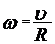 . (3)
. (3)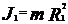 ,
, 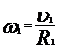 .
.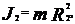
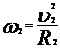 . (5)
. (5)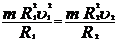 .
.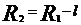 , окончательно имеем
, окончательно имеем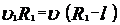 , откуда
, откуда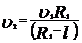 . (6)
. (6)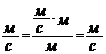 .
.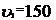
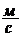 ,
, 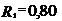
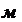 ,
, 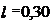
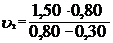
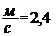
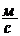 .
.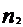 после укорачивания нити воспользуемся формулами
после укорачивания нити воспользуемся формулами 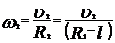 и
и 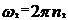 .
.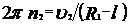 , откуда
, откуда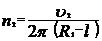 . (7)
. (7)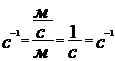 .
.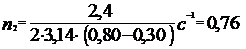
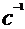 .
.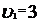
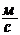 , ударился о стену и покатился назад со скоростью
, ударился о стену и покатился назад со скоростью 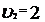
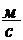 . Масса диска равна m=3 кг. Определить уменьшение кинетической энергии диска.
. Масса диска равна m=3 кг. Определить уменьшение кинетической энергии диска.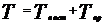 . (1)
. (1)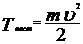 ;
; 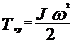 , где m- масса диска;
, где m- масса диска; 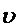 - скорость поступательного движения;
- скорость поступательного движения; 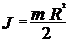 - момент инерции диска;
- момент инерции диска; 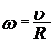 - угловая скорость диска; R- радиус окружности диска.
- угловая скорость диска; R- радиус окружности диска.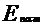 ,
, 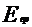 ,
, 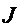 и
и 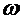 , получим
, получим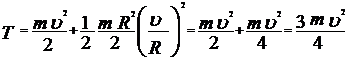 . (2)
. (2)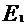 до удара о стену и полной кинетической энергии
до удара о стену и полной кинетической энергии 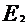 после взаимодействия со стеной:
после взаимодействия со стеной: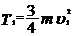 ,
, 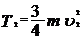 .
.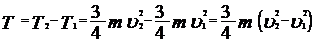 .
.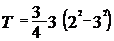 = - 11,25 Дж.
= - 11,25 Дж.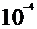 дж. 1. Найти амплитуду колебаний. 2. Написать уравнение данных колебаний. 3. Найти наибольшее значение силы, действующей на точку.
дж. 1. Найти амплитуду колебаний. 2. Написать уравнение данных колебаний. 3. Найти наибольшее значение силы, действующей на точку.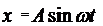 .
.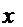 по времени, найдем скорость колеблющейся точки:
по времени, найдем скорость колеблющейся точки: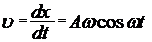 .
.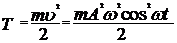 .
.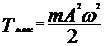 .
.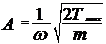 .
.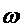 связана с периодом колебаний соотношением
связана с периодом колебаний соотношением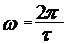 .
.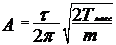 .
.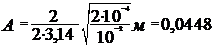
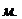
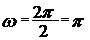 .
.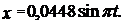
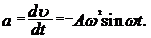
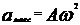 .
.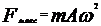 .
.