
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Доказать теорему о сумме внутренних углов треугольника.Теорема
Сумма внутренних углов выпуклого многоугольника, имеющего
Доказательство:
Если какую-то точку Свойства перпендикуляра и наклонной (без доказательства). Теорема - основное свойство перпендикуляра. Пусть А - некоторая точка, расположенная вне прямой l, В - точка на l такая, что прямая АВ перпендикулярна l, С - произвольная точка на l, отличная от В. Тогда АВ < АС. То, что прямая АВ перпендикулярна l, можно записать следующим образом: АВ ^ l. Точку В называют основанием перпендикуляра, опущенного из точки А на l, или проекцией точки А на l. Утверждение теоремы кратко выражают следующим образом: перпендикуляр меньше любой наклонной (наклонной является АС), или так: кратчайшим путем от точки к прямой является перпендикуляр к прямой. Теорема 1. Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой. Теорема 2. Если две наклонные, проведённые к прямой из одной и той же точки, равны, то равны и их проекции . Теорема 3 (обратная). Если две наклонные, проведённые к прямой из одной и той же точки, имеют равные проекции, то они равны между собой. Теорема 4. Если из одной и той же точки проведены к прямой две наклонные, то та из них больше, которая имеет большую проекцию на эту прямую.  Теорема 5 (обратная). Если из одной и той же точки проведены к прямой две наклонные, то большая наклонная имеет и большую проекцию на эту прямую. Доказать теорему об отношении площадей подобных многоугольников. Теорема об отношении площадей подобных треугольников: Для тех, кто не знает треугольники называются подобными, если 1. Два угла 1 треугольника соответственно равны 2 углам другого треугольника 2. Две стороны 1 треугольника пропорциональны 2 сторонам другого треугольника и углы, заключенные между сторонами, равны. 3. Три стороны 1 треугольника пропорциональны 3 сторона другого треугольника. Отношение площадей 2 подобных треугольников равно квадрату коэффициента подобия. Пусть треугольники ABC и А1В1С1 подобны, причем коэффициент подобия равен k O, обозначим буквами S и S1 площади этих треугольников. Так как A=A1, то S/S1 = AB*AC/A1B1*A1C1 (по тереме об отношении площадей треугольника). По формулам имеем: АВ/А1В1 = k, AC/A1C1 = k поэтому S/S1 = k2 Теорема доказана. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 272. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 сторон, равна
сторон, равна 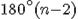 .
. внутри выпуклого многоугольника соединить со всеми вершинами, то получится столько же треугольников, сколько сторон у многоугольника
внутри выпуклого многоугольника соединить со всеми вершинами, то получится столько же треугольников, сколько сторон у многоугольника  . Сумма внутренних углов всех треугольников равна
. Сумма внутренних углов всех треугольников равна  , а сумма углов данного многоугольника меньше на
, а сумма углов данного многоугольника меньше на  (полный угол при вершине
(полный угол при вершине  .
.