
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема. Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.Стр 1 из 8Следующая ⇒ Геометрия.
Если при пересечении двух прямых секущей: 1) равны внутренние накрест лежащие углы; 2) равны соответственные углы; 3) сумма внутренних односторонних углов равна 180
Дано: При пересечении a и b секущей AB, накрест лежащие углы равны.
Док-ть: A параллельно b.
Док-во: 1) 2) Пусть
Площадь круга: S = πR2
Площадь сектора:
Площадь сегмента:
Теорема. Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют два прямых. Углы с соответственно параллельными сторонами либо равны друг другу ( если они оба острые, или оба тупые,
Формула длины окружности:
C=2pR C=pD
Формула длины дуги окружности:
 Теорема 3 (третий признак равенства — по гипотенузе и острому углу) Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны. Дано: Требуется доказать: Доказательство: Доказываем наложением Теорема 4 (четвёртый признак равенства — по гипотенузе и катету) Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны. Дано: Требуется доказать: Доказательство: Для доказательства применим способ приложения, которым был доказан признак равенства всяких треугольников. Приложим Из равенства наклонных
6. Формулы площади правильного многоугольника. Вписанный в окружность радиуса R:
Описанный около окружности радиуса r:
1-ый признак равенства треугольников(Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.).
Доказать: ΔABC=ΔA Доказательство: Так как
Правильный многоугольник, вписанный в окружность R:
Правильный многоугольник, описанный около окружности r:
Параллелограмм - это четырёхугольник, у которого противоположные стороны попарно параллельны. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Четырёхугольник — это геометрическая фигура, состоящая из четырёх точек, каждые три из которых не лежат на одной прямой, и четырёх непересекающихся отрезков, последовательно соединяющих эти точки, а также части плоскости, ограниченной этими отрезками. Различают выпуклые и невыпуклые четырёхугольники.
Теорема: Если у выпуклого четырехугольника диагонали пересекаются и точкой пересечения делятся пополам, то он является параллелограмм. Дано: AB, BC, CD, DA – стороны; AB и BD – диагонали.
Д-ть: Четырехугольник ABCD – параллелограмм.
Д-во: AB=DC,
Центральная симметрия или симметрия относительно точки (центра) – Z0 т. О – центр симметрии. Т. М и М1 называются симметричными относительно точки О, если т. О – середина отрезка ММ1, т.е. 1) симметричные точки и т. О принадлежит ММ1; 2) МО=ОМ1 Общие свойства · Центральная симметрия является движением (изометрией). · В n-мерном пространстве центральную симметрию можно представить как композицию n последовательных отражений относительно n взаимно перпендикулярныхгиперплоскостей, проходящих через центр симметрии. В частности · В чётномерных пространствах центральная симметрия сохраняет ориентацию, а в нечётномерных — не сохраняет. · Центральную симметрию можно представить также как гомотетию с центром A и коэффициентом −1 ( · Композиция двух центральных симметрий — параллельный перенос на удвоенный вектор из первого центра во второй:
Изоме́три́я, или движе́ние, или (реже) наложе́ние — биекция (преобразование), которая сохраняет расстояние между соответствующими точками, то есть если
Теорема. Сумма углов выпуклого n-угольника равна 180 Доказательство. Пусть дан выпуклый многоугольник А1А2А3…Аn. Данный n-угольник диагоналями, выходящими из одной вершины делится на (n – 2) треугольника так, как показано на рис. Сумма углов многоугольника состоит из суммы углов всех треугольников. Сумма углов каждого треугольника равна 180 Следствие. Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360 Сумма внутреннего и внешнего углов при каждой вершине n-угольника составляет 180 Поэтому сумма внешних углов n-угольника будет равна: 180 Значит, сумма внешних углов n-угольниками не зависит от числа n.
Любой
Где a, b, c – стороны,
Равнобедренный
Прямоугольный
Равносторонний
Прямоугольный равнобедренный
Ромб –параллелограмм, у которого все стороны равны. Параллелограмм –четырехугольник, у которого противолежащие стороны попарно параллельны.
Теорема. Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов. Доказательство. Пусть дан ромб ABCD, в котором AC и BD являются его диагоналями. Докажем, что AC На основании свойства параллелограмма имеем: AO=OC. Треугольник ACD равнобедренный, поэтому отрезок DO является в нем биссектрисой и высотой, т.е. DO
Осевая симметрияилисимметрия относительно прямой - |Sl| |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 515. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ; то эти прямые параллельны.
; то эти прямые параллельны.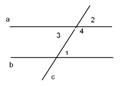 ИСПРАВИТЬ ЦЫФРЫ НА РИСУНКЕ!!!
ИСПРАВИТЬ ЦЫФРЫ НА РИСУНКЕ!!! 2 и
2 и 
 - для
- для 
 - для центрального угла в
- для центрального угла в 
 <180
<180 


 1 =
1 = 
 - для
- для  - для
- для  и
и  ,
,  ,
,  ,
, 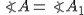 .
. .
. пойдёт по
пойдёт по  , так как
, так как  и
и  .
.  совпадёт с
совпадёт с  .
.
 .
. и
и  образуют одну прямую.
образуют одну прямую.  .
. и
и  следует:
следует:  . По трём сторонам или по двум катетам треугольники
. По трём сторонам или по двум катетам треугольники  и
и  равны.
равны.

 Дано:
Дано:
 B
B 
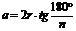
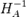 ).
).
 и
и 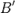 — образы точек
— образы точек  и
и  , то
, то  .
. Доказать теорему о сумме внутренних углов многоугольника.
Доказать теорему о сумме внутренних углов многоугольника. n - 180
n - 180  :
: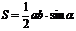

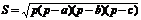

 , где R – радиус описанной окружности.
, где R – радиус описанной окружности. , где
, где  , где r – радиус вписанной окружности.
, где r – радиус вписанной окружности.




 BD и
BD и