Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема о скалярном произведении векторов. Следствие о перпендикулярных векторах (без доказательства).Определение. Два вектора называются перпендикулярными, если угол между ними равен 90o. Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними. Скалярное произведение векторов Теорема. Скалярное произведение векторов = Следствие 1. Ненулевые векторы Следствие 2. Косинус угла между ненулевыми векторами
Доказать формулу Герона. Формула Герона выражает площадь треугольника через длины трех его сторон. Теорема (формула Герона). Площадь треугольника со сторонами a, b, c и полупериметром p равна выражению: Доказательство. Пусть O - центр вписанной в треугольник ABC окружности, r - ее радиус . Соединив центр O с вершинами A, B и C, получим треугольники AOC, BOC и AOB с высотами, равными r. Согласно свойству площадей: пл. треугольника ABC=пл. треугольника AOC+пл. треугольника AOB+пл. треугольника BOC= = 1/2 b . r+1/2 c . r+1/2 a . r=r/2 (a+b+c)=p . r. Выражая r через стороны треугольника a, b и с, получаем Тогда , что и требовалось доказать. 38. Определение синуса, косинуса и тангенса для любого угла 0° до 180° (без доказательства). Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: 
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет
Доказать теорему об отрезках пересекающихся хорд. Хорда - отрезок, соединяющий две точки, лежащие на окружности. Теорема об отрезках хорд. Если две хорды одной окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство.
Проведём BC и AD.
Коллинеарные векторы. Теорема о разложении вектора по двум неколлинеарным векторам. Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»). Доказать теорему синусов. Теорема Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство. Пусть есть Δ ABC со сторонами a, b, с и углами α, β, γ. Докажем, что
Проведем из точки С высоту CD. Тогда из Δ ACD получим: Если угол α тупой, то
Из Δ BCD получаем
Аналогично получаем Теорема доказана. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 259. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  обозначается так:.
обозначается так:. 
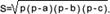

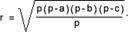
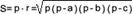
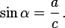
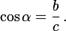


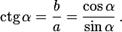
 , лежащий напротив угла
, лежащий напротив угла  , называется противолежащим (по отношению к углу
, называется противолежащим (по отношению к углу  , который лежит на одной из сторон угла
, который лежит на одной из сторон угла 
 по двум углам
по двум углам  (опираются на одну дугу) и
(опираются на одну дугу) и  (вертикальные) =>
(вертикальные) =>  =>.
=>.