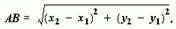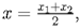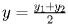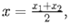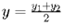Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Средняя линия трапеции параллельна основаниям и равна их полусумме.Д-ть: EF || AB, EF || CD; EF= Д-во:
BF = FC EF- ср. линия. EF || AB; EF || DC EO = EF = EO + OF =
Параллельный перенос фигуры Фназывается такое преобразование фигуры Ф, при котором все ее точки смещаются в одном и том же направлении на одно и то же расстояние.
Свойства параллельного переноса в пространстве. · Параллельный перенос есть движение. · При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую. · При параллельном переносе плоскость переходит либо в себя, либо в параллельную ей плоскость. · Параллельный перенос задается парой соответствующих точек, т.е. каковы бы ни были точки
Теорема.
Доказательство. 
Гомотетия с центром в точке О и коэффициентом k Свойства.
Теорема о свойстве касательной к окружности Теорема. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания. Дано: окр (О; ОА) P – Касательная к окружности, А – точка касания. Доказать: P перпендикулярна ОА. Доказательство (методом от противного) Предположим, что P не перпендикулярна ОА В этом случае радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведённый из точки О к прямой Р, меньше наклонной ОА, то расстояние от центра О окружности до прямой Р меньше радиуса. Следовательно, прямая Р. и окружность имеют две общие точки, т.е. Р – секущая. Но это противоречит условию теоремы, что Р. - касательная к окружности. Так как получили противоречие, то предположение, что Р не перпендикулярно ОА было неверным, значит, Р. перпендикулярна ОА. Итак, касательная к окружности перпендикулярна к радиусу, проведённому в точку касания. Ч.т.д. Верна и теорема, обратная теореме о свойстве касательной - признак касательной. Теорема. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. Дано: окр (О;ОА), Р, А принадлежит Р, Р перпендикулярна ОА Доказать: Р. – касательная к окр (О;ОА). Доказательство По условию Р принадлежит ОА, ОА – радиус окружности, поэтому расстояние от центра окружности до прямой Р равно радиусу ОА. Следовательно, прямая и окружность имеют только одну общую точку. А это означает, что данная прямая Р является касательной к окружности. Итак, если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. Ч.т.д.
Замечательными точками треугольника являются Точки пересечения: Медиан — центроид, центр масс; Биссектрис — инцентр, центр вписанной окружности; Высот — ортоцентр; Серединных перпендикуляров — центр описанной окружности; Cимедиан — точка Лемуана; Биссектрис серединого треугольника (его инцентра) — точка Шпикера; Точки пересечения отрезков, соединяющих вершины треугольника: c точками касания противоположных сторон и вписанной окружности — точка Жергонна; c точками касания противоположных сторон и вневписанной окружности — точка Нагеля; c соответствующими свободными вершинами равносторонних треугольников, построенных на сторонах треугольника (наружу) — первая точка Торичелли с соответствующими свободными вершинами правильных треугольников, построенных внутрь треугольника — вторая точка Торичелли. c соответствующими свободными вершинами треугольников, подобных исходному треугольнику и построенных на его сторонах — точки Брокара; Центр окружности девяти точек.
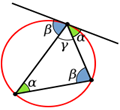
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°. Доказательство
Через вершину треугольника проведена касательная к описанной окружности Следствия: Через вершину треугольника проведена касательная к описанной окружности Вписанные углы, опирающиеся на одну дугу, равны. Угол, опирающийся на диаметр, — прямой. Гипотенуза прямоугольного треугольника является диаметром описанной около него окружности. Угол между касательной и хордой является предельным случаем вписанного угла и также равен половине дуги, на которую опирается. Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.
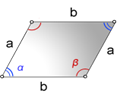
1. Формула площади параллелограмма через стороны и углы
a, b - стороны параллелограмма
α, β - углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
a, b - стороны параллелограмма
Hb - высота на сторону b
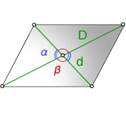
Ha - высота на сторону a Формула площади через стороны и высоты параллелограмма, (S): 3. Формула площади параллелограмма через диагонали и угол между ними
D - большая диагональ
d - меньшая диагональ
α, β - углы между диагоналями
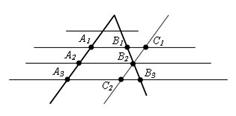
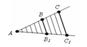
Теорема. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
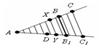
Доказательство. Пусть стороны угла A пересекаются параллельными прямыми в точках B, B1, C, C1. Теоремой утверждается, что
Разделим отрезок AC на n равных частей. Пусть δ – длинна отрезка деления и AC = nδ.
Возможны два случая: 1) Существует такое n, при котором B – точка деления. То есть существует m < n такое, что AB = mδ. Проведем через точки деления отрезка AC прямые, параллельные прямой CC1. По теореме Фалеса эти прямые разбивают отрезок AC1 на равные отрезки некоторой длины δ1. Получаем AB1 = mδ1, AC1 = nδ1. Из этого
2) Ни при каком n, B1 не является точкой деления. Допустим, что
Отложим на луче AC1 отрезок AD = (AC1/AC)*AB . При этом AD < AB1. Разобьем AC1 на достаточно большое число n равных частей. Проведем через точки деления прямые, параллельные СС1. При достаточно большом n на отрезке DB1 будут точки деления. Обозначим одну из них как точку Y и проведем через нее прямую параллельную СС1, которая пересекает луч AC в точке X. По доказанному
Заменим AY меньшей величиной AD, а AX большей величиной AB. Тогда
Отсюда
\ Что противоречит построению отрезка AD. Теорема доказана.
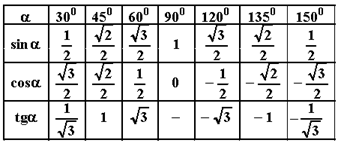
Тригонометрические формулы Основные тригонометрические тождества sin² α + cos² α = 1 tg α · ctg α = 1 tg α = sin α ÷ cos α ctg α = cos α ÷ sin α 1 + tg² α = 1 ÷ cos² α 1 + ctg² α = 1 ÷ sin² α Формулы сложения sin (α + β) = sin α · cos β + sin β · cos α sin (α - β) = sin α · cos β - sin β · cos α cos (α + β) = cos α · cos β - sin α · sin β cos (α - β) = cos α · cos β + sin α · sin β tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β) tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β) ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α) ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α) Формулы двойного угла cos 2α = cos² α - sin² α cos 2α = 2cos² α - 1 cos 2α = 1 - 2sin² α sin 2α = 2sin α · cos α tg 2α = (2tg α) ÷ (1 - tg² α) ctg 2α = (ctg² α - 1) ÷ (2ctg α) Формулы тройного угла sin 3α = 3sin α - 4sin³ α cos 3α = 4cos³ α - 3cos α tg 3α = (3tg α - tg³ α) ÷ (1 - 3tg² α) ctg 3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α) Формулы понижения степени sin² α = (1 - cos 2α) ÷ 2 sin³ α = (3sin α - sin 3α) ÷ 4 cos² α = (1 + cos 2α) ÷ 2 cos³ α = (3cos α + cos 3α) ÷ 4 sin² α · cos² α = (1 - cos 4α) ÷ 8 sin³ α · cos³ α = (3sin 2α - sin 6α) ÷ 32 Переход от произведения к сумме sin α · cos β = ½ (sin (α + β) + sin (α - β)) sin α · sin β = ½ (cos (α - β) - cos (α + β)) cos α · cos β = ½ (cos (α - β) + cos (α + β))
Второй признак подобия треугольников: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. Третий признак подобия треугольников: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
А] Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны
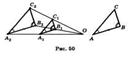
Первый признак подобия треугольников. Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны. Доказательство. Начало доказательства одинаково для всех трех признаков. Рассмотрим два треугольника ABC и A1B1C1, для которых выполняется одно из трех сформулированных условий (рис. 1). Причем будем считать, то обозначения выбраны следующим образом. Первый признак. Равны углы при вершинах A и A1, кроме того,
Отложим на луче AB отрезок AB2 = A1B1 и проведем через B2 прямую, параллельную BC. Получившийся треугольник AB2C2 подобен треугольнику ABC по основной теореме о подобных треугольниках. Нам остается доказать, то треугольник AB2C2 равен треугольнику A1B1C1 . Первый признак. В треугольниках A1B1C1 и AB2C2 равны углы при вершинах A и A1, A1B1 = AB2 . Кроме того, по условию,
Формула расстояния между двумя точками Пусть A и B -- две точки плоскости, координаты которых в декартовой системе координат: (x1; y1) и (x2; y2), тогда
Формула
Строгая формулировка Координаты середины отрезка с концами и находятся по формуле:
- координаты точки ; - координаты точки в декартовой системе координат на плоскости
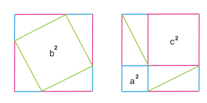
b2 = a2 + c2
В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c.
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 444. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (AB + CD).
(AB + CD).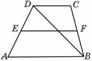 AE = ED (теор. Фалеса)
AE = ED (теор. Фалеса)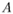 и
и 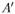 , существует единственный параллельный перенос, при котором точка
, существует единственный параллельный перенос, при котором точка 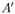 .
.
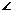 C1B2B1 =
C1B2B1 = 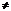 0называется такое преобразование, при котором каждая точка М отображается в такую точку М1, что выполняется равенство:
0называется такое преобразование, при котором каждая точка М отображается в такую точку М1, что выполняется равенство: 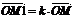

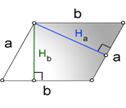 2. Формула площади параллелограмма через сторону и высоту
2. Формула площади параллелограмма через сторону и высоту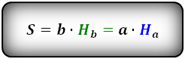
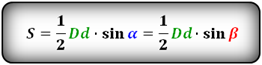
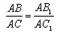
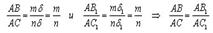
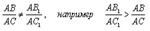
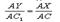
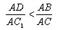

 Первый признак подобия треугольников: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Первый признак подобия треугольников: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
 .
.
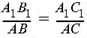
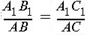 а из того, то треугольники AB2C2 и ABC подобны, следует равенство.
а из того, то треугольники AB2C2 и ABC подобны, следует равенство. 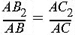 Из этих двух равенств получаем (так как A1B1 = AB2), то A1C1 = AC2. Значит, треугольники A1B1C1 и AB2C2 равны по первому признаку равенства треугольников.
Из этих двух равенств получаем (так как A1B1 = AB2), то A1C1 = AC2. Значит, треугольники A1B1C1 и AB2C2 равны по первому признаку равенства треугольников.