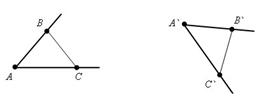Площадь квадрата, прямоугольника, трапеции (без доказательства).

квадрат: Квадра́т — правильный четырёхугольник или ромб, у которого все углы прямые, или параллелограмм, у которого все стороны и углы равны.

S = a2

S = d2 : 2

прямоугольник: Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).

S = ab

трапеция: Трапе́ция Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этовляется частным случаем трапеции.

S = h( a+b ) : 2

Площадь - это величина, численное значение которой обладает следующими свойствами:

равные фигуры имеют равные площади

если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей

плошадь квадрата со стороной, равной единице измерения, равна единице.

Равнобедренный треугольник. Свойства равнобедренного треугольника.

Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя — основанием. По определению, правильный треугольник также является равнобедренным, но обратное утверждение неверно.

Свойства

Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.

Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).

Соотношения между сторонами и углами прямоугольного треугольника (без доказательства).

Доказать теорему косинусов.

Теорема косинусов:

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Теорема Пифагора это частный случай теоремы косинусов о которой я поведу речь. Теорема косинусов имеет вид:

a2 = b2 + c2 - 2bc*Cos(A)

Cos(A) это угол лежаший напротив стороны a (обычное обозначение сторон и углов: напротив стороны "а" лежит угол A, "b" лежит угол B, "c" лежит угол C).

Доказательство теоремы не очень сложное, судите сами: Введем систему координат с началом в точке А так, как показано на рисунке. Тогда точка В имеет координаты (с;0), а точка С - (b cos A; b sin A). По формуле расстояния между двумя точками получаем

ВС2 = а2 = (b cos(A) - c)2 + b2Sin2(A) =

 = b2Cos2(A) + b2Sin2(A) - 2*bcCos(A) + c2 =

 = b2 + c2 - 2*bcCos(A)

Теорема доказана.

Движение. Свойства движения (без доказательства).

Теорема.

 Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

Доказательство.

 Пусть есть три точки A, B и С, которые лежат на одной прямой и точка B лежит между точками A и С.

Докажем, что точки A`, B` и C` лежат на одной прямой.

Если точки A`, B` и C` не лежат на одной прямой, то эти точки являются вершинами треугольника. Поэтому A`C`Докажем, что B` лежит между A` и C`. Тогда выполняются равенства AB=A`B`, AC=A`C`, BC=B`C`, AB+BC=AC. Отсюда следует, что A`B`+B`C`=A`C`. Это означает, что точка B` лежит между точками A` и C`.Теорема доказана.

 Следствие из теоремы

 1.Отрезок движением переводится в отрезок.

2.Луч при движении переходит в луч, прямая – в прямую.

3.Треугольник движением переводится в треугольник.

Теорема.

 При движении сохраняются углы между полупрямыми.

 Пусть полупрямые AB и BC не лежат на одной прямой и образуют угол. При движении полупрямые переходят в A`B` и A`C` соответственно. Проведем отрезок BC и B`C`. Получим треугольник ABC и A`B`C`. Так как при движении расстояния сохраняются, то треугольники ABC и A`B`C` равны по третьему признаку равенства треугольников, а следовательно углы ABC и A`B`C` равны. Теорема доказана