Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оптимизация параметров системы среднего калибра с присоединенной камерой подгона ⇐ ПредыдущаяСтр 9 из 9 Одной из схем, способных проводить модернизацию классического орудия без изменения внутренних геометрических параметров его ствола, обеспечивая при этом новый принцип дополнительного подгона снаряда, является схема с ускоряемыми камерами подгона Сафронов А.И., Крайнов А.Ю. Внутренняя баллистика установки среднего калибра // Вестник ТГПУ. 2004. №6. С. 173–179. На рис. 1.1. изображён продольный разрез артиллерийской системы СПК. Процесс выстрела в модернизированном орудии будет протекать в соответствии с описанием процесса выстрела СПК данным в подразделе 1.2. В данной главе приведено описание метода решения обратной задачи внутренней баллистики СПК, опирающееся на газодинамическую модель и методы нелинейного программирования. Эффективность предлагаемого подхода показана на примере проектирования 125-мм установки СПК с использованием штатных порохов. В данных системах существенное влияние на показатели выстрела оказывают волновые эффекты в газах, поэтому расчёт внутрибаллистических характеристик и определение оптимальных условий заряжания для СПК необходимо проводить по газодинамической модели. Решение ПЗВБ подобных систем проводится на основе модели газопороховой смеси. Особенности задачи учитываются при использовании комбинированной системы координат, индивидуальной для каждой из расчётных областей и связанной с левой границей соответствующей области (см. рис. 1.2.). Практически классическая схема выстрела позволяет метать из ПБУ с длинным стволом относительно тяжёлые снаряды с коэффициентом относительного веса Cq = 2 (кг/дм3) со скоростями около 2200 м/с при максимальных давлениях на дно канала до 500 МПа.  Таким образом, при ограничении максимальных давлений на дно канала до 1000 … 1200 МПа классическая схема выстрела не в состоянии обеспечить достижение скоростей метания относительно тяжёлых снарядов в диапазоне 2500 … 3000 м/с на системах с ограниченной длиной ствола. В случае применения СПК для метания относительно тяжёлых ПЭ с Cq = 2,7 (кг/дм3) были получены скорости 2620 м/с. В связи с этими данными, представляет интерес реализация подобных скоростей метания на установках СПК среднего и малого калибров с ограниченной длиной ствола. Учитывая ограничение длины ствола, целесообразно повысить давление в стволе и на дне канала рассматриваемых установок. Предполагалось, что максимальное давление на дно канала установки калибра 125 мм ограничено 1200 МПа, в области дополнительного заряда считалось допустимым давление 1000 МПа. Для артиллерийской установки калибра 125 мм был выбран объём каморы равный 34 дм3, а длина ствола считалась равной 6,1 м, масса снаряда составляла 5,9 кг (Cq = 3 кг/дм3). Для практики, в том числе и для модернизации существующих артиллерийских систем, представляет интерес задача определения параметров СПК в рамках фиксированной геометрии, поэтому при оптимальном внутрибаллистическом проектировании варьируем только условия заряжания и параметры схемы. Требуется максимизировать скорость снаряда
при ограничении на допустимые давления в основной камере, на правой границе поршня схемы и на снаряде
где р0 – давление на дно канала ствола. В качестве варьируемых параметров выберем величины
где w1, w2 – масса основного и дополнительного зарядов; Ik1, Ik2 – импульс пороха основного и дополнительного зарядов; tЗ – время задержки зажигания; h1, h2, h3, h4 – ограничения по давлениям на соответствующих границах расчётных областей. Варьирование параметров (2.7) проводим в области, определяемой ограничениями вида
где Для нахождения максимума (2.5) при ограничениях (2.6), определяемых на решениях системы (1.1) с граничными условиями (1.2), применяются поисковые методы нелинейного программирования, при этом нелинейные ограничения (2.6) учитываются с помощью квадратичной штрафной функции, линейные ограничения (2.8) - с помощью проектирования, а последовательность задач по максимизации штрафной функции вида F=UД – где Кi – штрафные множители – с применением Р – точечных алгоритмов оптимизации, не использующих в процессе поиска производные. Увеличивая Кi мы последовательно добиваемся более точного выполнения ограничений (2.6). В качестве примера в таблице 2.2 приведены значения управляющих параметров и показателей процесса выстрела при оптимизации модельной артиллерийской системы СПК калибра 125 мм. Показан вариант заряжания с параметрами `х0, удовлетворяющий ограничениям (4.8) и показывающий существенную чувствительность процесса к неоптимальному выбору `х. Результаты предварительного подбора параметров `хi приняты за начальное приближение для последующей оптимизации. Соответствующие расчётные баллистические параметры начальной точки приведены на рис. 2.2,а.
Таблица 2.1. Оптимизация параметров системы нетрадиционной схемы
В процессе оптимизации в первом приближении с коэффициентом штрафа Ki =5 получены параметры системы калибра 125 мм: VД = 2938 м/с, maxp0 = 1000МПа, maxp3 = 1250МПа. В дальнейших расчётах Ki увеличили до 69, что позволило более точно учесть ограничения (2.6). На заключительной стадии поиска оптимальных параметров масса основного заряда увеличилась на 3,1кг, масса поршня контейнера уменьшилась на 2,7 кг. Оптимальные параметры представлены вектором `х* в таблице. При этом реализована расчётная скорость снаряда VД = 2830 м/с. Баллистические параметры оптимальной точки приведены на рис. 4.2,б. Для сравнения с классической схемой выстрела был просчитан вариант с одинаковым по массе зарядом, что и при СПК, и подобрано одинаковое максимальное давление на дно канала ствола. Расчётная скорость снаряда при этом составила VД = 2358 м/с. Таким образом, выигрыш в скорости при СПК по сравнению с классической схемой достигает 20%. Определены параметры пороховой установки среднего калибра СПК, позволяющей метать снаряды с высокими скоростями в диапазоне сверхартиллерийских скоростей, при этом выигрыш в скорости по сравнению с классической схемой с теми же зарядом, массой снаряда и максимальным давлением на дно канала составляет 20%.
Заключение 1. Разработана математическая модель с использованием допущений гетерогенной среды для системы с присоединенной камерой подгона; 2. Определены оптимальные параметры СПК с использованием модели гетерогенной среды; 3. Выбран метод циклического покоординатного спуска для оптимизации рассматриваемой системы; 4. Для учета нелинейных ограничений использован метод штрафных функций; 5. Для учета линейных ограничений использован метод проектирования значения параметра на нарушенное ограничение. 6. В результате оптимизации достигнуто расчетное увеличение в скорости на 20% при неизменных максимальных давлениях на дно канала для системы калибра 125 мм.
Список использованной литературы
1. А.И. Сафронов, В.Г. Бутов, Н.М. Симонова. Оптимизация параметров системы для повышения скоростей метания элементов // Физика.– 2005.– № 11. Темат. вып.– С.41 – 44. 2. А.И. Сафронов, Н.М. Симонова, В.Г. Бутов. Оптимизация параметров системы для повышения скоростей метания элементов. Статья. печат. Известия ВУЗ Физика. Т.48.2005. № 11. 3. А.Н. Крайко, Р. И. Нигматулин, В.К. Старков, Л.Е. Стернин. Механика мнофазных сред // Итоги науки и техн. ВИНИТИ. Гидромеханика. 1972, с.93–174. 4. В.Г. Дулов. Распад произвольного разрыва параметров газа на скачке площади сечения. – Вестник ЛГУ, 1958, серия математики, механики и астрономии, № 19, с.76-Г00. 5. В.Н. Вилюнов. Теоретические основы зажигания, горения и газовой динамики РДТТ. – Дис. ... докт.физ. – мат.наук. – Томск, ТГУ, 1967, 557 с. 6. Высокоскоростное взаимодействие тел / В.М. Фомин, А.И. Гулидов, Г.А. Сапожников и др. Новосибирск: Изд – во СО РАН. 1999. 600с. 7. Вычислительные методы в гидромеханике. Сб. статей М.: ИЛ, 1964. 8. Газодинамические основы внутренней баллистики / С.А. Бетехтин, А.М. Виницкий, М.С. Горохов, К.П. Станюкович и др. – М.:Оборонгиз, 1957, 384с. 9. Дейч М.Е., Г.А. Филиппов. Газодинамика двухфазных сред. Изд.2–е, переб. и дополн. М.: Энергоиздат. 1981. 472 с. 10. Е.И. Погорелов. Об одном комбинированном алгоритме решения оптимальных задач внутренней газовой динамики//В кн.: Аэродинамика быстропротекающих процессов. Томск: Изд. Томского ун-та. 1982. С. 34 – 40. 11. И.Г. Русяк, B.М. Ушаков. Внутрикамерные гетерогенные процессы в ствольных системах. Екатеринбург: УрО РАН, 2001. 259 с. ISBN 5–7691–1210–7. 12. И.М. Васенин, В.А. Архипов, В.Г. Бутов, А.А. Глазунов, В.Ф. Трофимов. Газовая динамика двухфазных течений в соплах. Томск: Изд. Томск. ун-та. 1986, 262 с. 13. М. Базара, К. Шетти. Нелинейное программирование. Теория и алгоритмы: Пер. с англ. – М.: Мир, 1982. 583 с. 14. М.Е. Аэров, О.М. Тодес. Гидравлические и тепловые основы работы аппаратов со стационарным и кипящим зернистым слоем. – М. – Л.: Химия, 1968, с. 176. 15. М.Е. Серебряков. Внутренняя баллистика ствольных систем и пороховых ракет. – М.: Оборонгиз, 1962, 703 с. 16. Особенности описания двухфазных смесей в рамках односкоростной модели // И.Г. Русяк. Аэрогазодинамика быстропротекающих процессов. Сборник статей под ред. Л.В. Комаровского. Издательство Томского университета. 1982. 86 – 91. 17. Р.И. Нигматулин. Динамика многофазных сред. Ч.1.- М.: Наука, 1937, 464 с. 18. Р.И. Нигматулин. Методы механики сплошной среды для описания многофазных смесей. – Прикладная матем. и механика, 1970, т.34, с. 1097-1112. 19. Р.И. Нигматулин. Основы механики гетерогенных сред. // М.: Наука, 1978. 336с. 20. С.А. Ашманов, А.В. Тимохов. Теория оптимизации в задачах и упражнениях // М.: Наука. Гл. ред. физ. – мат. лит. , 1991. 448 с. 21. С.К. Годунов, А.В. Забродин и др. Численное решение многомерных задач газовой динамики.- М.: Наука, 1976, 400с. 22. Сверхзвуковые двухфазные течения в условиях скоростной неравновесности частиц / Н.Н. Яненко, Р.И. Солоухин, А.Н. Панырин, В.М. Фомин. Новосибирск: Наука, 1980, 160с. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 744. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
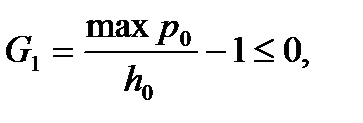


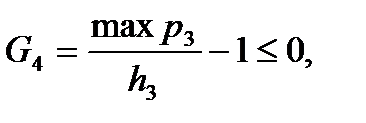
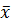 =
= 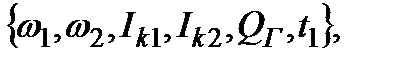
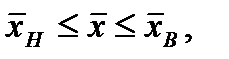
 – нижняя и верхняя границы, определяемые из физических соображений.
– нижняя и верхняя границы, определяемые из физических соображений. ,
,