Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм циклического покоординатного спускаРассмотрим алгоритм метода циклического покоординатного спуска для минимизации функции нескольких переменных, не требующий использования производных [21]. Для остановки алгоритма могут быть использованы несколько критериев. В приведенном ниже алгоритме процесс останавливается, если Начальный этап. Выбрать число e > 0, которое будет использоваться для остановки алгоритма, и взять в качестве d1, ..., dn координатные направления. Выбрать начальную точку х1, положить y1 = х1, k=j=1 и перейти к основному этапу. Основной этап. Шаг 1, Положить lj равным оптимальному решению задачи минимизации f(yj+ldj) при условии lÎE1.
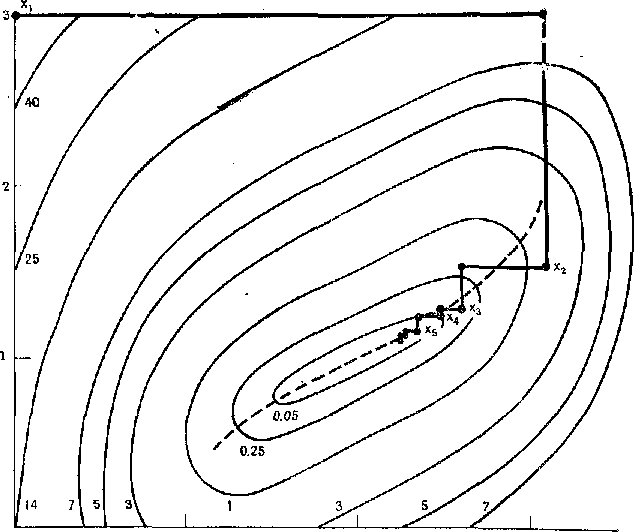
Положить уj+1=уj +ljdj. Если j < п, то заменить j на j+1и вернуться к шагу 1. Если j = n, то перейти к шагу 2. Шаг 2. Положить хk+1= уn+1. Если || хk+1 — хk ||< e то остановиться. В противном случае положить у1 = хk+1, j=1, заменить k на k+1 и перейти к шагу 1. Тестирование метода циклического покоординатного спуска Рассмотрим следующую задачу: минимизировать (х1 — 2)4 + (х1 — х2)2. Заметим, что оптимальным решением этой задачи является точка (2, 1), в которой значение функции равно нулю. В табл. 2.1. приведены результаты вычислений по методу циклического покоординатного спуска для начальной точки (0, 3). Заметим, что на каждой итерации векторы у2 и у3 получены посредством одномерной минимизации по направлениям (1, 0) и (0, 1) соответственно. Заметим также, что заметное убывание функции получено в течение первых нескольких итераций, тогда как на последних итерациях процесс явно замедляется. После семи итераций получена точка (2,13;1,059), 
значение функции в которой равно f = 0,0004296. На рис. 2.1. показаны лишь линии уровня целевой функции, точки и линии поиска, полученные методом циклического покоординатного спуска. Замедление на последних итерациях объясняется тем, что вдоль оврага, показанного пунктирной линией, делаются очень маленькие шаги по ортогональным направлениям. Метод штрафных функций Суть метода заключается в преобразовании исходной целевой функции посредством включения в нее функции от ограничений, получая, таким образом, задачу безусловной оптимизации [5, 21], для решения которой можно использовать рассмотренные в первой части методы. Переход от задачи условной оптимизации к задаче безусловной оптимизации осуществляется посредством включения в исходную функцию “штрафов” за нарушение ограничений задачи. Если исходная задача имеет следующий вид:
то преобразованная задача определится как:
где W - штрафная функция от ограничений задачи, а R - штрафной параметр. Наличие штрафного параметра R вызвано тем, что введение штрафной функции сильно деформирует поверхность целевой функции, что, в свою очередь, приводит к ухудшению обусловленности преобразованной задачи. Поэтому параметр R служит “регулятором” веса штрафной составляющей в целевой функции, и процесс решения задачи разбивается на ряд вспомогательных задач с различными значениями параметра R и контролем сходимости их решений. Наиболее распространенными являются следующие виды штрафов: квадратичный, логарифмический, штраф, заданный обратной функцией, штраф типа квадрата срезки. Квадратичный штраф используется для учета ограничений-равенств и имеет вид: F(R, h(x)) = R(h(x))2. Его значение резко возрастает при отклонении h(x) от нуля, однако, стационарная точка штрафной функции P(x,R) стремится к х* – стационарной точке исходной функции. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 615. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
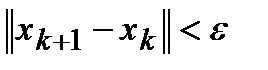 . Ясно, что можно применить и любой другой критерий остановки.
. Ясно, что можно применить и любой другой критерий остановки.