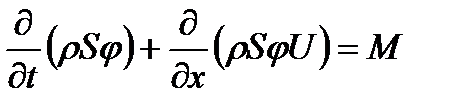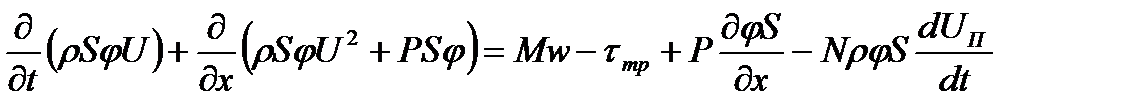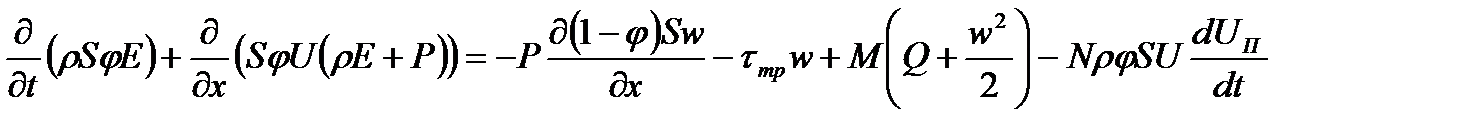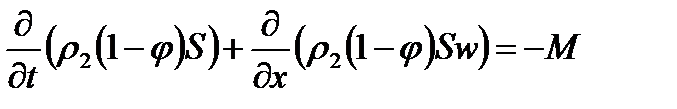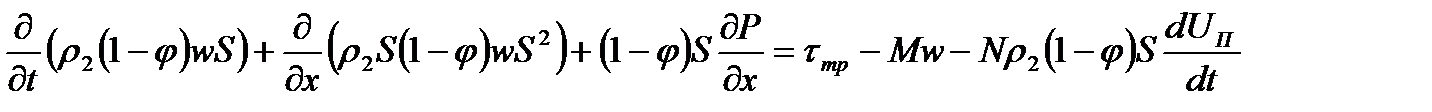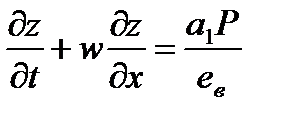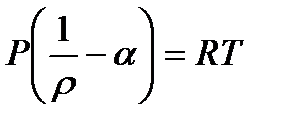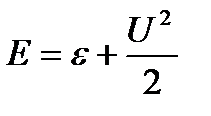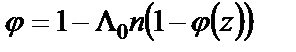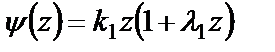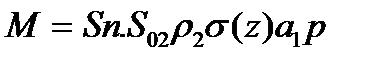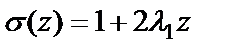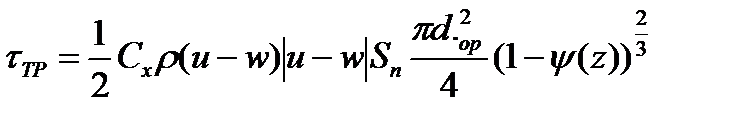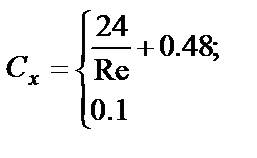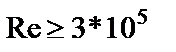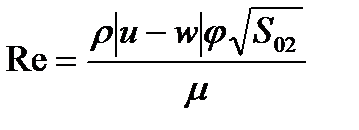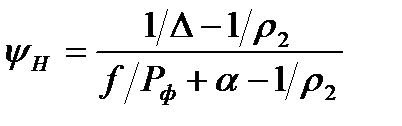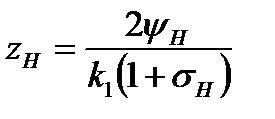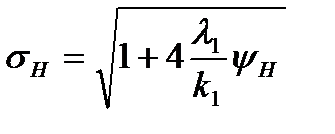Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
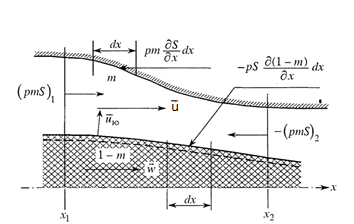
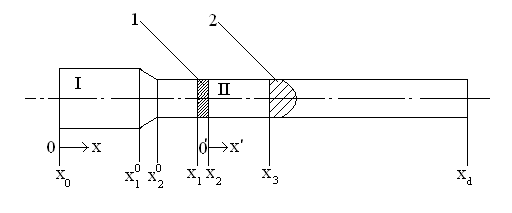
Математическая постановка задачиБудем рассматривать двухфазный поток, состоящий из пороховых газов и совокупности горящих частиц зерненного пороха, характерный размер и концентрация которых такова, что выполняется допущение. Дополнительно примем следующие допущения, связанные со спецификой задачи: 1) движения фаз одномерно; 2) теплоотдача к горящей поверхности зерен не учитывается (скорость движения тепловой волны в порохе равна скорости горения); 3) материал частиц несжимаем; 4) параметры газа внутри и вне пороховых элементов в данном сечении одинаковы. При выводе квазиодномерных уравнений двухфазной реагирующей смеси мы исходили из пространственной системы уравнения движения, которые не содержат члены, характеризующие взаимодействие со стенками канала ствола [11]. Поэтому дадим краткий вывод одномерных уравнений, где такое взаимодействие учитывается. В постановку задачи должны входить уравнения, полученные на основе законов сохранения массы, импульса и энергии для газа, а так же массы и количества движения для твердой фазы. В силу допущений 2), 3) уравнение энергии для твердой фазы не требуется. Рассмотрим одномерное течение двухфазной смеси в фиксированном объеме W, определенном координатами x1, x2 (рис. 1.2.) и ограниченном поверхностью Σ. Как показано выше, в однородной среде объемная пористость равна поверхностной. Данное утверждение, строго говоря, не выполняется на непроницаемых поверхностях (в нашем случае боковая поверхность канала). Тем не менее, будем считать, что гипотеза сплошной среды справедлива как угодно близко к боковой поверхности канала. Тогда, не смотря на не проницаемость стенок, можно принять, что пористость среды на стенке равна объемной пористости. Очевидно, данное предположения будет выполняться тем точнее, чем сильнее неравенство ℓ/dкн 
скольжения.
С учетом этих замечаний уравнения сохранения массы для обеих фаз внутри объема W имеют вид:
Уравнения импульсов каждой из фаз можно представить аналогичным образом:
где В одномерном случае силу межфазного взаимодействия, приходящуюся на единичный объем гетерогенной среды, необходимо представить так:
где первая составляющая обусловлена разностью скоростей между фазами, вторая – давлением газа в связи с расширением или сужением трубки тока второй фазы (рис. 1.2.). Полная энергия смеси в объеме W изменяется за счет притока энергии извне, работы сил давления на ограничивающей поверхности Σ, притока химической энергии за счет горения пороховых зерен, теплообмена с поверхностью канала и расхода механической энергии твердой фазы за счет трения «газа частиц» о поверхности ствола. Итак,
где qc – тепловой поток на поверхность канала ствола. Последний член уравнения (1.6) записан для математической корректности. Его отсутствие при постоянной внутренней энергии твердой фазы означало бы, что работа сил трения частиц о поверхность ствола способствует повышению энергии газа, тогда как единственно возможный механизм передачи энергии между фазами – это межфазовое взаимодействие. Реально тепло, связанное с этим членом, идет на нагрев материалов ствола и пороховых частиц при соударении. Этими эффектами будем пренебрегать. Используя теорему о градиенте:
справедливую для непрерывных подынтегральных функций в W и на Σ, в одномерном случае получаем
где Для остальных поверхностных интегралов соответствующая теорема Гаусса–Остроградского неприменима, так как подынтегральные функции терпят разрыв при переходе на боковую поверхность ограничивающей поверхности Σ. Их можно расписать следующим образом, например:
Интеграл по боковой поверхности обращается в нуль, так как на стенке
Полученная система уравнений содержит семь неизвестных: параметры газа В практических расчетах для зерненых порохов удобно заменить уравнения неразрывности твердой фазы уравнением для счетной концетрации пороховых элементов :
тогда пористость смеси определится из выражения
1.3. Моделирование системы с присоединенной камерой подгона при использовании подхода механики гетерогенных сред Схема с присоединённой камерой подгона позволяет повышать начальные скорости метания элементов. Рассмотрим возможность получения выигрыша в начальной скорости метания элемента для модельной установки с использованием присоединённой камеры подгона при неизменном максимальном давлении на дно закрытого торца цилиндрического канала [12]. В этом случае решается задача движения метаемого элемента по цилиндрическому каналу под действием газов, образующихся при постепенном горении топлива в двух областях.
Разделение общей массы заряда на две части является частным случаем. Возможно рассмотрение трёх и более областей. Между двумя частями топлива помещается поршень. Он совершает движение по цилиндрическому каналу под действием давления газов, образующихся в результате сгорания топлива. В начальный момент времени в движение приходит вся сборка, состоящая из присоединённой камеры подгона (поршень + заряд второй области) и метаемого элемента. Через некоторый промежуток времени t3 (время задержки зажигания) воспламеняется заряд в присоединённой камере подгона (назовём его присоединённым), в результате давление во второй области повышается. В момент, когда сила сопротивления становится больше силы, ускоряющей сборку, последняя разделяется: метаемый элемент отделяется и движется вперёд самостоятельно, а поршень притормаживается. При достижении метаемым элементом конца ствола процесс заканчивается. Основным положительным свойством этого процесса является то, что за счёт работы присоединённого заряда происходит перераспределение энергии: часть её идёт на дополнительное ускорение МЭ, вследствие чего достигается выигрыш в скорости. Математическое моделирование схемы с присоединённой камерой подгона основано на подходе механики гетерогенных сред, модифицированном для внутренней баллистики ствольных систем, и проводится при следующих основных допущениях: - движение камеры подгона (поршень + присоединённый заряд) и метаемого элемента начинается при достижении давления форсирования; - начальный период для основного и присоединённого зарядов не учитывается; - горение частиц пороха происходит по геометрическому закону; - вязкость и теплопроводность существенны только в процессах взаимодействия фаз; - до момента разделения сборки частицы присоединённого заряда неподвижны относительно сборки; - после разделения сборки частицы присоединённого заряда могут выпадать на поршень; при равенстве пористости некоторой предельной величине вблизи поршня частицы начинают двигаться со скоростью поршня до тех пор, пока пористость не станет выше предельной; - при движении элементов схемы метания (сборки, затем поршня и метаемого элемента) не учитываются трение и сопротивление воздуха в стволе; - присоединённый заряд воспламеняется мгновенно в момент времени, соответствующий времени задержки зажигания; Система уравнений – процессы в области I – записывается в инерциальной системе координат (0, х), в области II – в неинерциальной системе координат (0, х'), связанной с поршнем. Приведём систему уравнений, которая при N= 0 описывает процессы в области I, а при N=1 и замене переменных и параметров на переменные и параметры со штрихом «'»(
где t – время; х – координата; р – давление; ρ – плотность; ρ2 – плотность вещества топлива; Т – температура; T0 – температура горения топлива; U – скорость газа; w – скорость частиц; φ – пористость; Е,ε – полная и внутренняя энергия единицы объёма газа; S – площадь поперечного сечения канала; z – относительная толщина сгоревшего свода; М – скорость массоприхода от горения топлива; τтр – сила взаимодействия между фазами; N – признак системы координат; dUn/dt-ускорение поршня; Q – тепловой эффект горения топлива; R – газовая постоянная; α – коволюм; а1 –коэффициент в законе скорости горения; ев – толщина горящего свода зерна топлива; п – концентрация; Λ0 – начальный объём частицы топлива; Ψ(z) –относительный сгоревший объём частицы топлива; k1, λ1 – коэффициенты формы частиц топлива; S02 – начальная площадь частиц топлива; σ(z) – относительная горящая поверхность частицы топлива; Сх – коэффициент сопротивления; d0P – диаметр шара эквивалентного по объёму частице топлива; Re – число Рейнольдса; μ – вязкость газа. Начальные условия в области I:
Для области II:
где Δ- плотность заряжания; f – сила топлива; Рф – давление форсирования; н – начальные значения переменных и параметров, G – газа. Граничные условия:
где хп – координата положения левой границы поршня; хs – координата положения дна метаемого элемента; Uп – скорость поршня; us - скорость метаемого элемента; п-параметры поршня, s-метаемого элемента.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 535. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
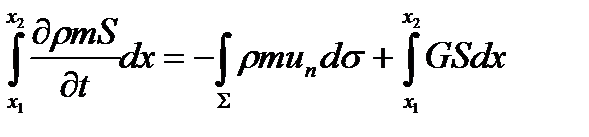
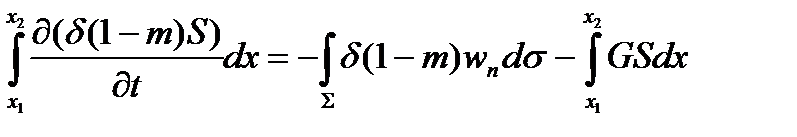
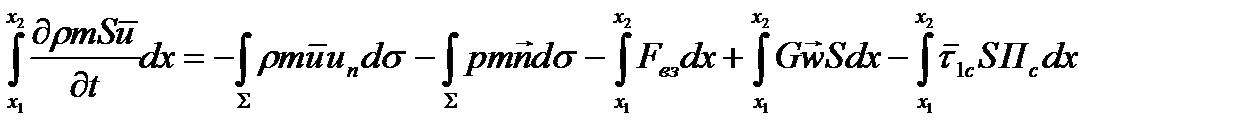
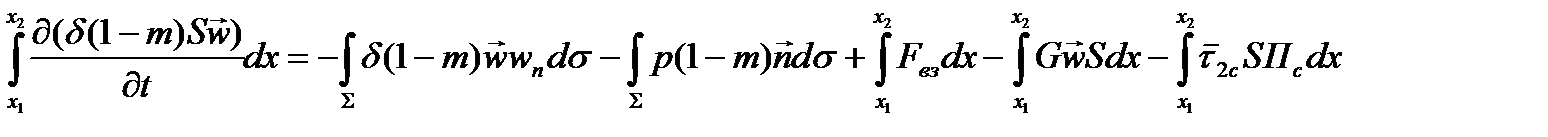
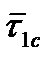 ,
, 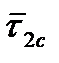 – векторы сил трения газа и пороховых частиц о поверхность ствола, приходящиеся на единицу площади соответственно.
– векторы сил трения газа и пороховых частиц о поверхность ствола, приходящиеся на единицу площади соответственно.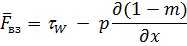
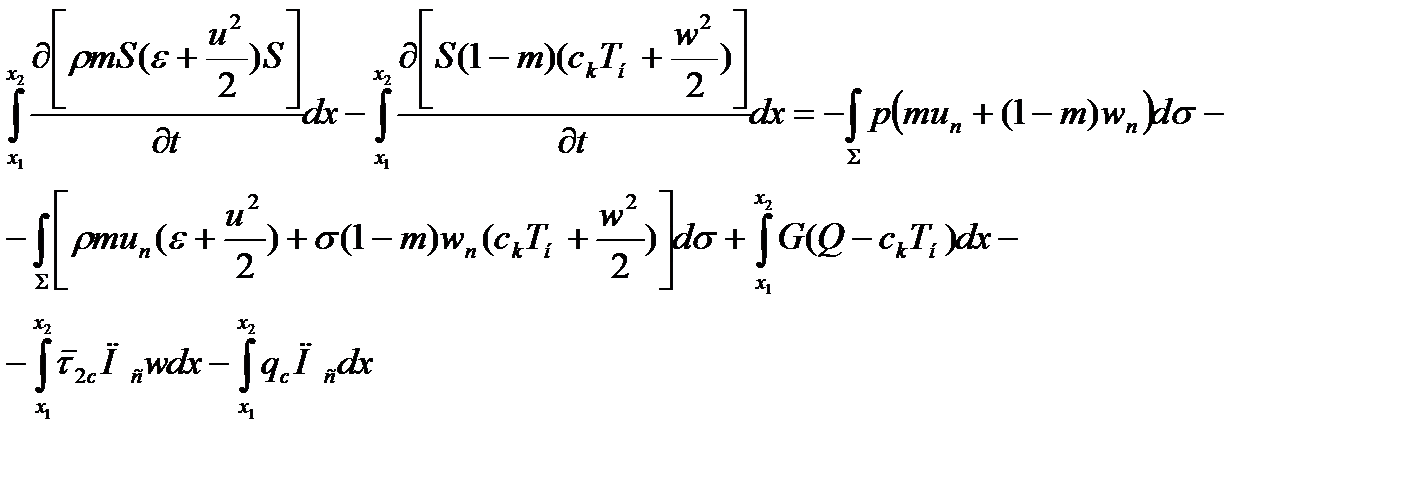
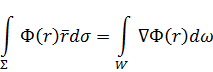
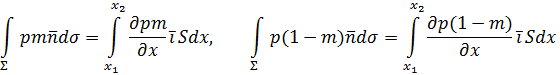
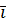 – единичный вектор в направлении оси x.
– единичный вектор в направлении оси x.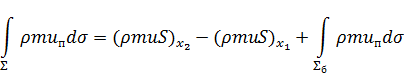
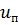 =0.
=0.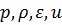 скорость твердой фазы w, пористость смеси m и относительную долю сгоревшего пороха
скорость твердой фазы w, пористость смеси m и относительную долю сгоревшего пороха 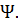
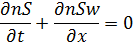
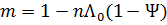
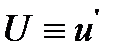 и т.д.) – процессы в области присоединённого заряда (область II) после его воспламенения.
и т.д.) – процессы в области присоединённого заряда (область II) после его воспламенения.