
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод циклического покоординатного спускаРассмотрим метод решения максимизации функции нескольких переменных f, не использующий вычисление производных [19]. Описанный здесь метод заключается в следующем. При заданном векторе Задача линейного поиска заключается в минимизации f ( В этом методе в качестве направлений поиска используются координатные векторы. Точнее, метод осуществляет поиск вдоль направлений d1, ..., dn, где dj — вектор, все компоненты которого, за исключением j-й, равны нулю. Таким образом, при поиске по направлению dj меняется только переменная хj, в то время как все остальные переменные остаются зафиксированными. Схематически этот метод проиллюстрирован на рис. 2.1.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 520. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
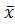 определяется допустимое направление
определяется допустимое направление 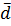 . Затем, отправляясь из точки
. Затем, отправляясь из точки 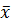 , функция f минимизируется вдоль направления
, функция f минимизируется вдоль направления