
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГЛАВА 1. Постановка задачи определения параметров системы с присоединенной камерой подгонаСтр 1 из 9Следующая ⇒ АННОТАЦИЯ В дипломной работе рассмотрена нетрадиционная схема метания, позволяющая осуществить увеличение начальной (дульной) скорости метаемого элемента. На основе разработанной математической модели систем с присоединенными камерами подгона поставлена задача оптимизации параметров подобных систем. Приведены и проанализированы методы оптимизации с учетом линейных и нелинейных ограничений для рассматриваемых систем. Выигрыш в начальной скорости для рассматриваемой системы получается за счет оптимизации параметров заряжания системы. Оглавление Условные обозначения. 5 Введение. 8 ГЛАВА 1. Постановка задачи определения параметров системы с присоединенной камерой подгона. 16 1.1. Физическая постановка задачи для системы с присоединенной камерой подгона 16 1.2. Математическая постановка задачи. 19 1.3. Моделирование системы с присоединенной камерой подгона при использовании подхода механики гетерогенных сред. 25 1.4. Метод решения прямой задачи внутренней баллистики. 31 ГЛАВА 2. Оптимизация параметров баллистической системы с камерой подгона 34 2.1. Постановка задачи определения оптимальных параметров в системах СПК с максимальной начальной скоростью метаемого элемента. 34 2.2. Метод циклического покоординатного спуска. 36 2.3. Алгоритм циклического покоординатного спуска. 37 2.5. Алгоритм метода штрафных функций. 41 2.6. Оптимизация параметров системы среднего калибра с присоединенной камерой подгона 44 Сноски. 51 Список использованной литературы.. 53
Условные обозначения t, t – время; х – Эйлерова координата; δ – плотность пороха;  u – скорость газа; w – скорость твёрдой фазы; r – плотность; р – давление; e, Е –внутренняя и полная энергия, соответственно; φ,m – пористость; n – концентрация; f – сила пороха; П=f/(k-1) – потенциал пороха; с – скорость звука в газе; S – площадь поперечного сечения канала; Т – абсолютная температура; R0, R – универсальная газовая постоянная; σ(z) – относительная площадь горящего зерна; eВ – толщина горящего свода высокоэнергетического состава; S02 – начальная площадь горящей поверхности зерна; κ1, λ1, μ1 – характеристики формы зерна заряда; Λ0, Λ02 – начальный объем частиц к-фазы; dоp – диаметр шара, эквивалентный начальному объёму зерна заряда; a1, ν – коэффициенты в законе скорости горения; M – массовая скорость горения; τтр – сила, действующая на частицу со стороны газа; Q – тепловой эффект от сгорания пороха; qт – тепловой поток из газовой фазы в зёрна заряда; Re – число Рейнольдса; cx – коэффициент сопротивления; tВ – момент времени воспламенения дополнительного заряда; xП – координата левой границы поршня; xS – координата положения дна метаемого элемента; uП – скорость поршня; uS – скорость метаемого элемента; qП, qS – массы поршня и МЭ; ω 1, ω2, ω3 – массы частей заряда; D = w/W – плотность заряжания; где W – объём камеры; mСБ = qП + ω2 + qS – масса сборки; P1, P2, P3, Рф – давления на поршень слева, поршень справа, на дно МЭ, давление форсирования соответственно; y - весовая доля сгоревшего пороха; z – относительная часть сгоревшего свода пороха; IК – конечный импульс давления; a – коволюм;
Индексы d – означает, что параметры берутся на дульном срезе; ′ – параметры и переменные относятся к области II; н – начальные условия; s – поверхность зерна; к – относится к к-фазе.
Введение
Вопросы освоения космического пространства, получения новых материалов, защиты объектов от террористических актов требуют изучения возможностей получения высоких скоростей метаемых тел в земных условиях, высокоскоростного взаимодействия тел, взаимодействия тел с преградами. В связи с этим, вопрос повышения скоростей метания тел будет актуальным всегда [1]. Вместе с тем, повышение скоростей метания тел очень сложная задача. Математическое моделирование процессов метания помогает вскрывать основные закономерности функционирования классических и нетрадиционных схем подгона, формулировать требования к конструкции и рабочим телам для получения необходимого эффекта и, таким образом, ограничивать область рассматриваемых решений. Проблеме повышения начальных скоростей метания тел при выстреле постоянно уделяется большое внимание. Эта проблема решается как путём совершенствования классического выстрела, так и путём создания принципиально новых нетрадиционных схем. Одной из схем, удачно сочетающей классическую баллистическую установку и принцип дополнительного подгона, является схема с ускоряемыми камерами подгона (СПК). Схема с ускоряемыми камерами подгона может быть реализована с зарядами из обычных типов высокоэнергетических составов. Определение баллистики систем СПК необходимо проводить газодинамическими методами в отличие от термодинамического подхода, при котором производится усреднение параметров по всему рабочему объему камеры высокого давления. Газодинамический метод позволяет определять параметры систем нетрадиционных схем метания с точностью, приемлемой для практики. В ряде прикладных задач при описании движения смеси газа и горящих частиц используется гипотеза газопороховой смеси. То есть считается, что скорости фаз в каждый момент времени в любой точке пространства одинаковы. Данное допущение существенно упрощает математическое описание соответствующих явлений и численную реализацию уравнений. Однако в рамках такого подхода невозможно исследовать влияние геометрии включений на параметры потока, а также исследовать процессы, связанные с относительным движением фаз: воспламенение, теплообмен, эрозию и т. д. Кроме того, неизвестна ошибка, которую вносит это допущение в конечное решение задачи. В свою очередь, основы механики многоскоростных континуумов к настоящему времени достаточно хорошо разработаны и могут с успехом применяться для описания гетерогенных сред. Запишем одномерную систему уравнений с учетом массового и силового взаимодействия фаз в предложении, что теплообмен со стенками канала отсутствует.
Система (1) получена при допущении, что среднеобъемная температура твердой фазы не меняется (скорость движения тепловой волны равна скорости горения). Здесь Используя систему (1), рассмотрим следствия, вытекающие из допущения w = u. Для этого уравнения движения фаз с помощью уравнений неразрывности перепишем следующим образом:
Откуда при условии w = u находим конечное выражение для функции силового взаимодействия
Из (2) в случае гипотезы газопороховой смеси имеем
Таким образом, допущение w = u эквивалентно заданию конечной функции силового взаимодействия с бесконечным коэффициентом сопротивления [2]. Рассмотрим задачу о движении поршня в трубе под действием давления, развиваемого горящими частицами, со следующими начальными и граничными условиями:
Здесь q — масса поршня. При численной реализации системы (1) совместно с (3) уравнения аппроксимировались разностной схемой совместно Эйлера Лагранжа [3].
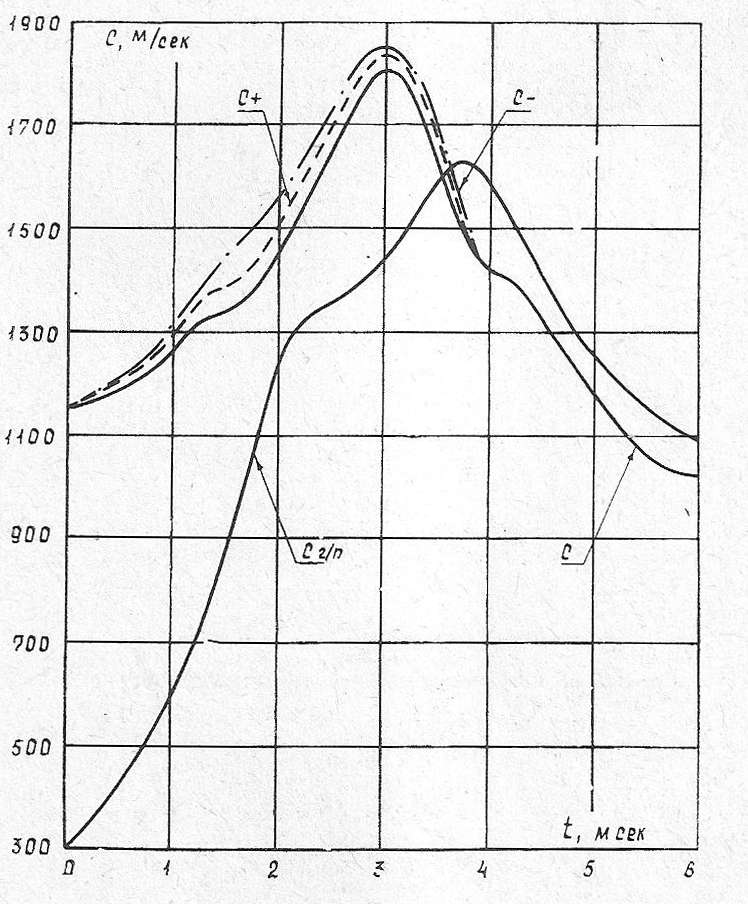
Рис. 1. Изменение скорости распространения возмущений со временем
На рис. 1 представлен характер изменения скоростей распространения возмущений со временем в сечении х=0,8 Ln для односкоростной Нетрудно показать, что «мощность» волны разрежения определяется акустическим импедансом [4]
где
откуда следует, что в случае гипотезы газопороховой смеси падение давления в волне разрежения в
Рис. 2. Изменение давления на дно канала со временем
Необходимо заметить, что точность решения системы (1) зависит от точности задания функции силового взаимодействия, т. е. от значения сх. Однако уже то обстоятельство, что любое конечное значение сх ближе к истинному, говорит о том, что двухскоростная модель описания гетерогенных смесей является более предпочтительной, даже если сх известно с большой погрешностью. Возможность повышения начальных скоростей метания обеспечивает использование систем со схемой СПК. В дипломной работе поставлена ПЗВБ систем СПК для модели гетерогенной среды. Представляет интерес также постановка и результаты решения задач по оптимальному проектированию баллистических установок СПК. В основу предлагаемого подхода заложена газодинамическая гетерогенная модель процесса и численные методы решения оптимальных и краевых задач. Методы одномерной оптимизации условно подразделяются на тригруппы [5]. К первой группе относятся методы, основанные лишь навычислении значений самой функции f(x) (методы нулевого порядка). - метод случайного поиска - метод деформируемого многогранника - метод конфигураций - циклического покоординатного спуска Вторую группу составляют методы, использующие значение как самойфункции, так и ее первой производной (методы первого порядка). - метод градиентного спуска; - метод наискорейшего градиентного спуска; - метод Гаусса-Зейделя; - метод сопряженных градиентов. И,наконец, к третьей группе относятся методы, использующие значениефункции, ее первой и второй производной (методы второго порядка). - метод Ньютона; - метод Ньютона-Рафсона; - метод Марквардта Обычно в процессе применения методов одномерной оптимизацииможно выделить два этапа: поиск отрезка, содержащего точку максимума,и уменьшение длины отрезка до заранее установленной величины(уточнение координаты точки максимума на данном отрезке). Метод не использующий производные. Данный метод просто последовательно проводит одномерную оптимизацию по каждой координате функции. Так, если функция f=f(x,y), то на каждом шаге этого метода сначала функция минимизируется в направлении оси x, а потом - оси y.Поиск точки минимума определяется рекуррентным соотношением Под задачей оптимального проектирования установки СПК понимается задача выбора следующих основных элементов: - массы метаемого тела; - параметров рабочих тел в камерах; - времен или координат задержек зажигания; - массы и конструкции поршней; - начальных условий в зарядных камерах. Эти элементы установки должны быть выбраны таким образом, чтобы обеспечить, например, максимально возможный уровень скоростей, при этом основными ограничивающими условиями являются прочность метаемого тела, камер подгона и зарядной камеры. Экспериментальный путь решения сформулированной задачи, или метод физического моделирования, основан на изготовлении и испытании установок, исходя из теоретических представлений о процессе и имеющегося опыта. Однако экспериментальный поиск основных элементов конструкции значительно удлиняет и удорожает процесс проектирования, а сложность проведения эксперимента и регистрации выходных характеристик ограничивают количество варьируемых параметров. В данной работе решение задач проектирования установки СПК проводится современными численными методами оптимизации, что с учетом возросших возможностей ПЭВМ позволяет значительно сократить сроки научных и конструкторских разработок, проанализировать основные пути повышения эффективности установок и оценить их экстремальные возможности. В математическом отношении задачи проектирования формулируются как задачи многокритериальной оптимизации процесса метания. Эффективность методов проверена на тестовых задачах. Ранее было показано [6], что за счет оптимизации можно значительно увеличить начальную скорость при неизменном максимальном давлении газа на метаемое тело и дно канала системы СПК. В дипломной работе рассмотрена задача проектирования установки по шести параметрам. В рамках принятой математической модели найдены новые оптимальные параметры систем СПК.
ГЛАВА 1. Постановка задачи определения параметров системы с присоединенной камерой подгона |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 560. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
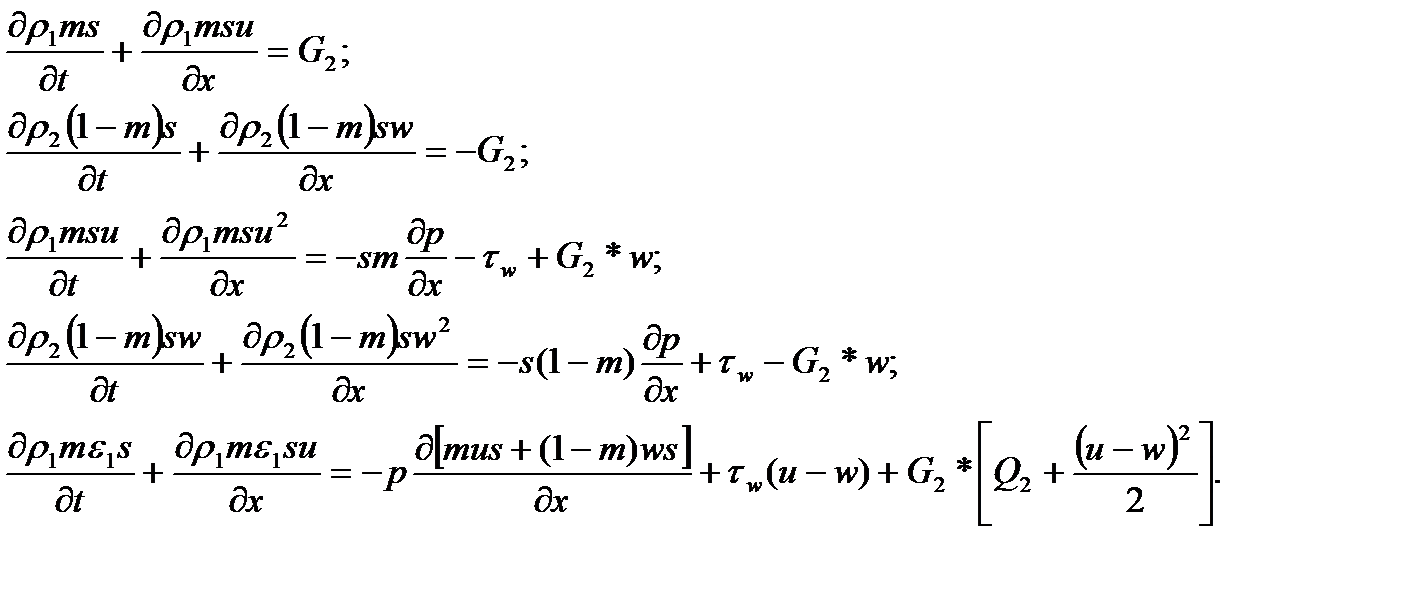 (1)
(1)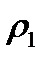 ,
, 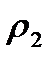 — соответственно истинные плотности газа (первой фазы) и несгоревших зерен (второй фазы); u, w — скорости первой и второй фазы; m — порозность; s — площадь сечения канала; р — давление;
— соответственно истинные плотности газа (первой фазы) и несгоревших зерен (второй фазы); u, w — скорости первой и второй фазы; m — порозность; s — площадь сечения канала; р — давление; 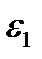 — внутренняя энергия первой фазы, приходящаяся на единицу массы; Q2 — теплотворная способность твердой фазы.
— внутренняя энергия первой фазы, приходящаяся на единицу массы; Q2 — теплотворная способность твердой фазы.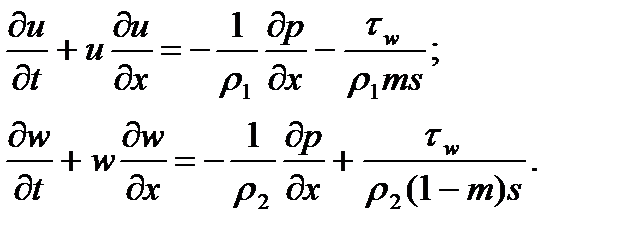
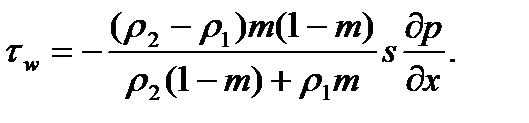 (2)
(2)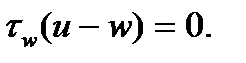
 ,
, 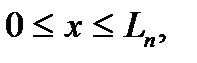
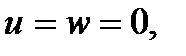
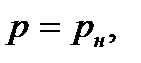
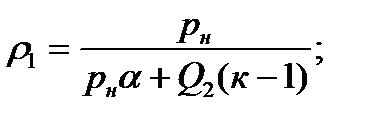 (3)
(3)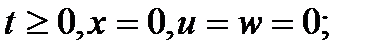
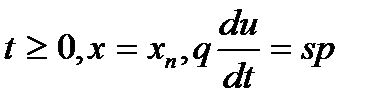
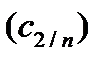 и двухскоростной
и двухскоростной 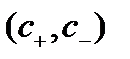 моделей течения. Для сравнения там же нанесена кривая скорости распространения возмущения (с) в чистом газе.
моделей течения. Для сравнения там же нанесена кривая скорости распространения возмущения (с) в чистом газе.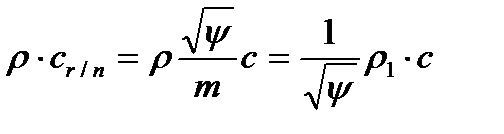 при
при 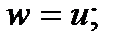
 — суммарная плотность смеси и
— суммарная плотность смеси и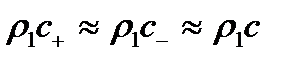 при
при 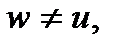
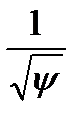 раз больше, чем в случае двухфазного течения. Значительные отличия в скорости передачи возмущений и в «мощности» волны разрежения существенно искажают характер решения рассматриваемой задачи. Сравнение результатов дано на рис. 2. Наличие на кривых угловых точек, «а» обусловлено движением волны разрежения, возбуждаемой поршнем. Точки «б» соответствуют моменту конца горения пороха. Из сопоставления графиков видно, что при достижении волной разрежения дна канала или дна поршня происходит падение давления в соответствующей области.
раз больше, чем в случае двухфазного течения. Значительные отличия в скорости передачи возмущений и в «мощности» волны разрежения существенно искажают характер решения рассматриваемой задачи. Сравнение результатов дано на рис. 2. Наличие на кривых угловых точек, «а» обусловлено движением волны разрежения, возбуждаемой поршнем. Точки «б» соответствуют моменту конца горения пороха. Из сопоставления графиков видно, что при достижении волной разрежения дна канала или дна поршня происходит падение давления в соответствующей области.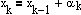 . Здесь
. Здесь 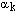 определяется из решения задачи одномерной оптимизации
определяется из решения задачи одномерной оптимизации 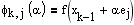 , где ej - вектора стандартного базиса в Rn. Отметим, что данный алгоритм эффективен в тех случаях, когда целевая функция является сепарабельной, т.е. может быть представлена в виде суммы функций, зависящих только от одной координаты.
, где ej - вектора стандартного базиса в Rn. Отметим, что данный алгоритм эффективен в тех случаях, когда целевая функция является сепарабельной, т.е. может быть представлена в виде суммы функций, зависящих только от одной координаты.