
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 26. Сравнение двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки)
1. По двум независимым выборкам, объем которых n = 40 и m = 50, извлеченным из нормальных генеральных совокупностей найдены выборочные средние Отв. zкр = 2,58. Выборочные средние различаются значимо.
2. По выборке объема n = 30 найден средний вес Отв. Zнабл = 2,5; zкр = 1,96. Нулевая гипотеза отвергается. Средний вес изделий различается значимо.
3. По выборке объема n = 50 найден средний вес Отв. Zнабл = 1,2; zкр = 1,96. Данные наблюдений согласуются с нулевой гипотезой; выборочные средние различаются незначимо.
Тема 27. Сравнение двух средних генеральных совокупностей, дисперсии которых известны (малые независимые выборки)
 1. По двум независимым малым выборкам, объемы которых n = 12 и m = 18, извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные средние Отв. Нулевая гипотеза о равенстве средних отвергается.
2. По двум независимым малым выборкам, объемы которых n = 10 и m = 8, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние Отв. Fнабл = 1,23; Fкр(0,01; 7; 9) = 5,62. Нет оснований отвергнуть гипотезу о равенстве дисперсий. Имеем |Тнабл| = 3,7; tдвуст.кр(0,01; 16) = 2,92. Нулевая гипотеза о равенстве средних отвергается.
3. Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены малые выборки, объемы которых n = 10 и m = 12. Получены следующие результаты:
Требуется, при уровне значимости 0,02, проверить гипотезу H0: M(X) = M(Y) о равенстве средних размеров изделий при конкурирующей гипотезе H1: M(X) ≠ M(Y). Отв. Средние размеры изделий существенно не различаются.
4. На уровне значимости 0,05, требуется проверить нулевую гипотезу H0: M(X) = M(Y) о равенстве генеральных средних нормальных совокупностей X и Y при конкурирующей гипотезе H1: M(X) > M(Y) по малым независимым выборкам, объемы которых n = 10 и m = 16. Получены следующие результаты:
Отв. Нет оснований принять или отвергнуть гипотезу. Следует увеличить объем выборки.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 2412. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
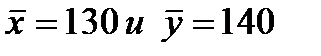 . Генеральные дисперсии известны: D(X) = 80, D(Y) = 100. Требуется, при уровне значимости 0,01, проверить нулевую гипотезу H0: M(X) = M (Y), при конкурирующей гипотезе H0: M(X) ≠ M (Y).
. Генеральные дисперсии известны: D(X) = 80, D(Y) = 100. Требуется, при уровне значимости 0,01, проверить нулевую гипотезу H0: M(X) = M (Y), при конкурирующей гипотезе H0: M(X) ≠ M (Y).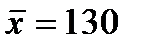 г изделий, изготовленных на первом станке; по выборке объема m = 40 найден средний вес
г изделий, изготовленных на первом станке; по выборке объема m = 40 найден средний вес 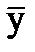 = 125г изделий, изготовленных на втором станке. Генеральные дисперсии известны: D(X) = 60г2, D(Y) = 80г2. Требуется, при уровне значимости 0,05, проверить нулевую гипотезу H0: M(X) = M (Y) при конкурирующей гипотезе M(X) ≠ M (Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.
= 125г изделий, изготовленных на втором станке. Генеральные дисперсии известны: D(X) = 60г2, D(Y) = 80г2. Требуется, при уровне значимости 0,05, проверить нулевую гипотезу H0: M(X) = M (Y) при конкурирующей гипотезе M(X) ≠ M (Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.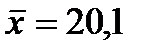 мм диаметра валиков, изготовленных автоматом №1; по выборке объема m = 50 найден средний размер
мм диаметра валиков, изготовленных автоматом №1; по выборке объема m = 50 найден средний размер 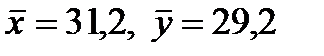 и исправленные дисперсии S2X = 0,84 и S2Y = 0,40. Требуется, при уровне значимости 0,05, проверить нулевую гипотезу H0: M(X) = M(Y) при конкурирующей гипотезе H1: M(X) ≠ M(Y).
и исправленные дисперсии S2X = 0,84 и S2Y = 0,40. Требуется, при уровне значимости 0,05, проверить нулевую гипотезу H0: M(X) = M(Y) при конкурирующей гипотезе H1: M(X) ≠ M(Y).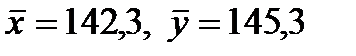 и исправленные дисперсии S2X = 2,7 и S2Y = 3,2. При уровне значимости 0,01, проверить нулевую гипотезу H0: M(X) = M(Y) при конкурирующей гипотезе H1: M(X) ≠ M(Y).
и исправленные дисперсии S2X = 2,7 и S2Y = 3,2. При уровне значимости 0,01, проверить нулевую гипотезу H0: M(X) = M(Y) при конкурирующей гипотезе H1: M(X) ≠ M(Y).