Магнитное поле прямого тока
 Применим формулу (1.4) для вычисления магнитной индукции поля прямого тока, т.е. поля, создаваемого током, текущим по тонкому прямому отрезку провода (рис. 1.4). В произвольной точке Применим формулу (1.4) для вычисления магнитной индукции поля прямого тока, т.е. поля, создаваемого током, текущим по тонкому прямому отрезку провода (рис. 1.4). В произвольной точке 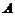 , удаленной от оси проводника на расстояние , удаленной от оси проводника на расстояние 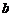 , векторы , векторы 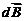 от всех элементов тока имеют одинаковое направление («на читателя»). Поэтому сложение векторов от всех элементов тока имеют одинаковое направление («на читателя»). Поэтому сложение векторов 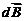 можно заменить сложением их модулей. Из рис. 1.4 видно, что можно заменить сложением их модулей. Из рис. 1.4 видно, что
 , ,  . .
Подставив эти выражения в формулу (1.4), получим:

Угол 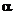 для всех элементов отрезка прямого тока изменяется в пределах от для всех элементов отрезка прямого тока изменяется в пределах от  до до  , поэтому , поэтому
 . .
Для случая прямого провода бесконечной длины  , ,  и, согласно последнему выражению, магнитная индукция определяется формулой: и, согласно последнему выражению, магнитная индукция определяется формулой:
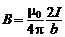 . .
Магнитное поле контура с током
 Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиусом Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиусом 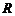 (круговой ток). На рис. 1.5 показан вектор (круговой ток). На рис. 1.5 показан вектор 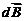 от элемента тока от элемента тока  , находящегося справа. От всех элементов тока будет образовываться конус векторов , находящегося справа. От всех элементов тока будет образовываться конус векторов 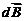 и результирующий вектор и результирующий вектор  в точке в точке 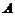 будет направлен вверх по оси будет направлен вверх по оси  . Это значит, что для нахождения модуля вектора . Это значит, что для нахождения модуля вектора  достаточно сложить проекции векторов достаточно сложить проекции векторов 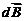 на ось на ось  . Каждая такая проекция определяется по формуле: . Каждая такая проекция определяется по формуле:
 , ,
где учтено, что угол между 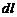 и и 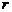 равен равен  , поэтому синус равен единице. Интегрируя это выражение по , поэтому синус равен единице. Интегрируя это выражение по 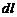 (что даст (что даст 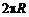 ) и учитывая, что ) и учитывая, что  и и 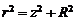 , получаем: , получаем:
 , ,
 . .
Отсюда следует, что в центре витка с током  и на расстоянии и на расстоянии 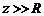 модуль вектора модуль вектора  равен соответственно: равен соответственно:
 . .
Закон Ампера
 Действие магнитного поля на рамку с током – это пример воздействия магнитного поля на проводник с током. Ампер установил, что сила Действие магнитного поля на рамку с током – это пример воздействия магнитного поля на проводник с током. Ампер установил, что сила  , с которой магнитное поле действует на элемент проводника , с которой магнитное поле действует на элемент проводника 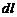 с током, находящегося в магнитном поле, равна: с током, находящегося в магнитном поле, равна:
 , (1.5) , (1.5)
где 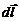 – вектор по модулю равный – вектор по модулю равный 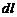 и совпадающий по направлению с током; и совпадающий по направлению с током;  – вектор магнитной индукции. – вектор магнитной индукции.
 Силу (1.5) называют силой Ампера, ее модуль вычисляется по формуле: Силу (1.5) называют силой Ампера, ее модуль вычисляется по формуле:
 , (1.6) , (1.6)
где 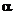 – угол между векторами – угол между векторами 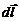 и и  . .
Направление силы Ампера перпендикулярно направлению тока (направлению 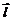 ) и направлению индукции ) и направлению индукции  и подчиняется правилу буравчика. Можно также пользоваться правилом левой руки (рис. 1.6): если ладонь левой руки расположить так, чтобы в нее входил вектор и подчиняется правилу буравчика. Можно также пользоваться правилом левой руки (рис. 1.6): если ладонь левой руки расположить так, чтобы в нее входил вектор  , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера. , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера.
Взаимодействие параллельных токов
Закон Ампера применяется для определения силы взаимодействия двух токов.
Два параллельных проводника с силой тока 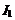 и и 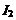 находятся на расстоянии находятся на расстоянии 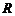 друг от друга. Направление сил друг от друга. Направление сил  и и  , с которыми поля , с которыми поля 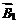 и и  действуют на проводники с силой тока действуют на проводники с силой тока 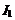 и и 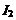 , определяются по правилу левой руки (рис. 1.7). , определяются по правилу левой руки (рис. 1.7).
 Если расстояние между токами Если расстояние между токами 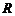 , то каждый элемент тока будет находиться в магнитном поле, индукция которого равна , то каждый элемент тока будет находиться в магнитном поле, индукция которого равна  . Угол . Угол 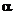 между элементами тока между элементами тока 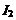 и вектором и вектором  – прямой. Следовательно, согласно формуле (1.6), на единицу длины тока – прямой. Следовательно, согласно формуле (1.6), на единицу длины тока 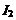 действует сила действует сила  , что совпадает с формулой (1.1). , что совпадает с формулой (1.1).
Для силы 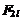 , действующей на единицу длины тока , действующей на единицу длины тока 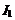 , получается аналогичное выражение. Легко убедиться в том, что при одинаковом направлении силы тока они притягивают друг друга, а при различном – отталкивают. , получается аналогичное выражение. Легко убедиться в том, что при одинаковом направлении силы тока они притягивают друг друга, а при различном – отталкивают.
|


 Применим формулу (1.4) для вычисления магнитной индукции поля прямого тока, т.е. поля, создаваемого током, текущим по тонкому прямому отрезку провода (рис. 1.4). В произвольной точке
Применим формулу (1.4) для вычисления магнитной индукции поля прямого тока, т.е. поля, создаваемого током, текущим по тонкому прямому отрезку провода (рис. 1.4). В произвольной точке 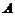 , удаленной от оси проводника на расстояние
, удаленной от оси проводника на расстояние 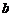 , векторы
, векторы 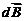 от всех элементов тока имеют одинаковое направление («на читателя»). Поэтому сложение векторов
от всех элементов тока имеют одинаковое направление («на читателя»). Поэтому сложение векторов  ,
,  .
.
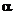 для всех элементов отрезка прямого тока изменяется в пределах от
для всех элементов отрезка прямого тока изменяется в пределах от  до
до  , поэтому
, поэтому .
. ,
,  и, согласно последнему выражению, магнитная индукция определяется формулой:
и, согласно последнему выражению, магнитная индукция определяется формулой: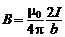 .
. Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиусом
Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиусом 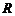 (круговой ток). На рис. 1.5 показан вектор
(круговой ток). На рис. 1.5 показан вектор  , находящегося справа. От всех элементов тока будет образовываться конус векторов
, находящегося справа. От всех элементов тока будет образовываться конус векторов  в точке
в точке  . Это значит, что для нахождения модуля вектора
. Это значит, что для нахождения модуля вектора  ,
,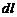 и
и 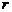 равен
равен  , поэтому синус равен единице. Интегрируя это выражение по
, поэтому синус равен единице. Интегрируя это выражение по 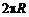 ) и учитывая, что
) и учитывая, что  и
и 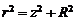 , получаем:
, получаем: ,
, .
. и на расстоянии
и на расстоянии 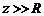 модуль вектора
модуль вектора  .
. Действие магнитного поля на рамку с током – это пример воздействия магнитного поля на проводник с током. Ампер установил, что сила
Действие магнитного поля на рамку с током – это пример воздействия магнитного поля на проводник с током. Ампер установил, что сила  , с которой магнитное поле действует на элемент проводника
, с которой магнитное поле действует на элемент проводника  , (1.5)
, (1.5)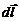 – вектор по модулю равный
– вектор по модулю равный  Силу (1.5) называют силой Ампера, ее модуль вычисляется по формуле:
Силу (1.5) называют силой Ампера, ее модуль вычисляется по формуле: , (1.6)
, (1.6)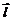 ) и направлению индукции
) и направлению индукции 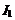 и
и 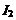 находятся на расстоянии
находятся на расстоянии  и
и  , с которыми поля
, с которыми поля 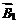 и
и  действуют на проводники с силой тока
действуют на проводники с силой тока  Если расстояние между токами
Если расстояние между токами  . Угол
. Угол  – прямой. Следовательно, согласно формуле (1.6), на единицу длины тока
– прямой. Следовательно, согласно формуле (1.6), на единицу длины тока  , что совпадает с формулой (1.1).
, что совпадает с формулой (1.1).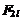 , действующей на единицу длины тока
, действующей на единицу длины тока