
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТЕМА 11. УЗАГАЛЬНЕНІ ЕКОНОМЕТРИЧНІ МОДЕЛІЛабораторна робота №22. Нелінійні моделі Приклади рішення задач Задача 11.1 (множинна нелінійна залежність між попитом та ціною на деякій товар) Нехай на повний вигляд товару таблиця попиту має вигляд:
де Рі- ціна за одиницю товару Dі - кількість товару поданого за певний період по ціні Рі 1. На основі статистичних даних знайти оцінки параметрів регресії попит, якщо допустити, що вона має таку структуру: D=a0+a1P+a2P2 (11.1) 2.Зробити повний регресійний, дисперсійний та економічний аналіз моделі. 3. Обчислити: - проміжки цін зростання та спадання товарообігу в грошовому вираженні; - ціну на товар, за якої товарообіг у грошовому вираженні буде максимальним; - проміжки цін зростання та спадання прибутку; - оцінку ціни на товар, за якої прибуток буде максимальним, та його значення. Рішення 1. Згідно теорії перетворимо вхідні данні залежності попиту від ціни в лінійну модель і заповнимо наступну таблицю. Таблиця 11.1
де Застосовуючи пакет аналіз «Регресія» табличного процесору Excel отримали наступні дані (табл. 11.2) Таблиця 11.2 Результати регресійного дисперсійного аналізу моделі
2.Аналіз даних робиться на основі прикладів рішення задач лабораторної роботи 18-22 (Задача 10.1) 3. Згідно даним таблиці 11.2: а0=8,97 а1=-0,78 а2=0,01 отже рівняння нелінійної залежності між попитом та ціною на деякий вид продукції має вигляд:
4.Для пошуку проміжків зростання та спадання товарообігу в грошовому вираженні підставимо значення знайдених оцінок параметрів регресії у формулу:
Маємо:Р1=51,64 Р2=6,41. Після підстановки отриманих значень у рівняння товарообігу, що дорівнює : Отримаємо два значення товарообігу одне максимальне , друге мінімальне.
Отже в точці Р1=51,64 товарообіг мінімальний а в точці Р2=6,41- максимальний. Проміжки зростання (враховуючі, що ціна – значення не від’ємне, теж саме стосується і товарообороту) товарообігу При р=13,6 значення товарообігу приблизно дорівнюватиме 0. 5. Для пошуку максимального прибутку скористуємося формулою: де С –сталі витрати, а VD – змінні витрати в собівартості продукції, та:
Підставляючи ці значення в формулу прибутку, знаходимо його похідну по Р і прирівнюємо до 0. Рішення квадратного рівняння має наступний вигляд:
а V – коефіцієнт змінних витрат пропорційний обсягу випуску продукції. Підставляючи отримані оцінки параметрів моделі маємо, наближено вираз значення ціни при найбільшому прибутку:
Отже чім більше значення V, тим більше ціна, так як підкореневий виріз завжди невід’ємний. Якщо відома собівартість продукції і відповідно її змінні витрати, то можна обчислити максимальний прибуток:
де Задача 11.2На основі статистичних даних показника Y і факторів Таблиця 11.3
Використовуючи критерій Фішера, оцінити з надійністю р = 0,95 адекватність прийнятої математичної моделі статистичним даним. Якщо модель адекватна, то знайти: — оцінки прогнозу та з надійністю р= 0,95 його надійний інтервал; — оцінки частинних коефіцієнтів еластичності для прогнозу. Рішення Вводиться гіпотеза, що між факторами Хь Х2 та показником У існує така стохастична залежність: Y=LN( Для розв'язування задачі використовуємо пакет прикладних програм Регресія, меню Сервіс/Аналіз даних табличного процесора Excel. Для приведення регресії до лінійного виду пропотенціюємо регресії та зробимо заміну величин
Застосовуючи пакет регресія для перетворених даних отримали оцінки параметрів лінійної регресії виду:
У даному прикладі розрахунку лінія регресії матиме вигляд У = 1n(0,1 + 0,02/ Згідно табличного значення критерія Фішера, що дорівнює: 12132,4. Можна зробити висновок про адекватність моделі статистичним даним. Знайдемо формули для частинних коефіцієнтів еластичності:
Для обчислення прогнозу підставимо прогнозні значення у формулу, маємо: Для обчислення помилки прогнозу за допомогою матричних функцій табличного процесора введемо: =КОРЕНЬ(1+МУМНОЖ(МУМНОЖ(
Завдання для самостійної роботи 1. Завдання вище описаного прикладу (задача 11.1) виконати для наступних статистичних даних ціни та кількості деякого проданого в певний період товару.( N- порядковий номер студента у журналі).Обчислити проміжки зростання та спадання прибутку, якщо в собівартості продукції С= 2,1 Таблиця 11.4
Де Записати отримані залежності та відповіді у зошит: ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 2. На основі статистичних даних показника Y і факторів Використовуючи критерій Фішера, оцінити з надійністю р = 0,95 адекватність прийнятої математичної моделі статистичним даним. Якщо модель адекватна, то знайти: — оцінки прогнозу та з надійністю р= 0,95 його надійний інтервал; — оцінки частинних коефіцієнтів еластичності для прогнозу. Записати отримані залежності та відповіді у зошит:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 297. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
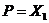 ,
, 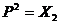 .
.
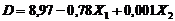 (11.2)
(11.2)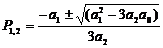 ) (11.3)
) (11.3)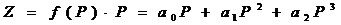
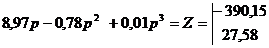
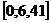 та спадання
та спадання  .
. (11.4)
(11.4)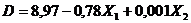
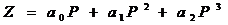
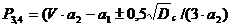 (11.5)
(11.5)
 (11.6)
(11.6)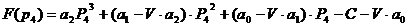
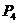 обчислено за формулою (11.2) при заданому значення V І с (С= 2,1 од. а, V= 0,7).
обчислено за формулою (11.2) при заданому значення V І с (С= 2,1 од. а, V= 0,7).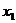 та
та 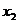 знайти оцінки параметрів регресії, якщо припустити, що стохастична залежність між факторами і показником має вигляд У = 1п(а0 +а1/Х1+ а2Х2) на основі вхідних даних:.
знайти оцінки параметрів регресії, якщо припустити, що стохастична залежність між факторами і показником має вигляд У = 1п(а0 +а1/Х1+ а2Х2) на основі вхідних даних:.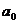 +
+ 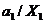 +
+  )
)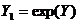
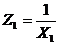

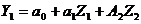
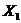 +2,6
+2,6  ).
).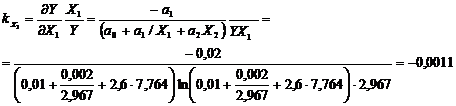
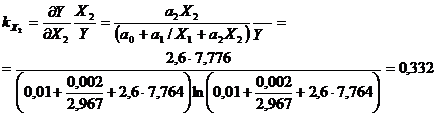
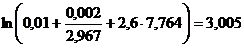 .
.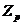 ;МОБР(МУМНОЖ(ТРАНСП(
;МОБР(МУМНОЖ(ТРАНСП(  );
); 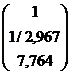 , а
, а 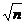 од. а, V= 0,7
од. а, V= 0,7 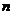 - порядковий номер вашого прізвища у журналі
- порядковий номер вашого прізвища у журналі