
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТЕМА 10. ЛІНІЙНІ МОДЕЛІ МНОЖИННОЇ РЕГРЕСІЇСтр 1 из 7Следующая ⇒ ЗМІСТОВИЙ МОДУЛЬ. ЕКОНОМЕТРИЧНІ МОДЕЛІ
ТЕМА 9 ПРИНЦИПИ ПОБУДОВИ ЕКОНОМЕТРИЧНИХ МОДЕЛЕЙ. ПАРНА ЛІНІЙНА РЕГРЕСІЯ Лабораторна робота №16-17. Парна лінійна регресія Приклади розв’язування задач Задача 9.1. (знаходження оцінок параметрів моделі) Знайти оцінки параметрів моделі
Рішення Нехай залежність між Х та У описується
Для обчислень можна використовувати таку допоміжну таблицю. Для перевірки таблиця вже має заповнені стовпці. Таблиця 9.1
 Обчислимо значення оцінок параметрів моделі за допомогою відхилень середніх арифметичних , за формулою:
та
Що дорівнює відповідно 5,33. Обчислимо значення Ур (розрахункове) використовую формулу .
Обчислимо залишки за формулою = У-Ур та їх квадрати, та відповідні суми стовпців. Обчислимо не зсунену оцінку дисперсії залишків
Коефіцієнт кореляції обчислимо за формулою (9.2):
=0,986 (9.2)
Коефіцієнт еластичності для парної регресії обчислимо за формулою:
Задача 9.2.(перевірка якості, точності та надійності моделі) На основі моделі попередньої задачі виконати наступне: - перевірити гіпотезу про значущість коефіцієнта кореляції, оцінок параметрів моделі (за допомогою t – тест Стюдента); - знайти інтервал довіри для параметра кутового коефіцієнта регресії, надійні межі для вільного члена; - перевірити модель на адекватність статистичним даним (F – тест, значущість 95%) - знайти точковий прогноз та інтервал довіри окремого значення Упр та для математичного сподівання значення Упр якщо Хпр=15. Рішення Для перевірки гіпотези про значущості коефіцієнта кореляції застосуємо формулу:
Порівняємо це значення з табличним значенням t (статистичні таблиці) якій дорівнює 2,306 и зробимо висновок. Для перевірки гіпотези про значущість оцінок параметрів моделі застуємо формулу:
Отже маємо: Порівняємо ці значення з табличним значенням критерію Стюдента (2,306) – зробимо висновки. Довірчий інтервал прогнозу будується на основі загального співвідношення: ŷ де Воно є базовим і використовується для визначення довірчих інтервалів прогнозу, побудованих за допомогою будь-яких моделей лінійної регресії, знайдених за методом найменших квадратів. Доведено, що для парної лінійної моделі гранична помилка прогнозу з достовірністю
При цьому застосовується табличне значення t – критерію Стьюдента з рівнем значущості ( Отже кутовий коефіцієнт нашої моделі знаходиться в межах (1,696; 1,7934), а вільний член попадає в інтервал довіри: (4,109; 6,56). Для розрахунку F критерію скористуємося формулою:
Порівнюючи отримане значення з табличним значенням критерію Фішера =3,4, (так як воно більше ніж розрахункове) , робимо висновок про адекватність моделі статистичним даним. Для розрахунку прогнозного значення У підставте прогнозне значення х=15 в отриману формулу регресії ( з завдання 1) :
Маємо Тоді надійний інтервал для математичного сподівання прогнозного значення дорівнює:
значення t критерію не змінюється =2,34. Середнє квадратичне відхилення, обчислене в попередньому завданні та інші складові формули знайдіть в рядку Сум в таблиці 9.1 з відповідними стовпцями. І в розрахунках вашої роботи. Завдання для самостійної роботи На основі прикладів розв’язування задач 9.1 та 9.2 виконати наступні завдання в табличному процесорі Excel: 1. Знайти оцінки параметрів моделі · значущість коефіцієнта кореляції; · значущість оцінок параметрів моделі; · адекватність моделі статистичним даним; · знайти інтервал довіри для параметра кутового коефіцієнта регресії; · надійні межі для вільного члена; · інтервал довіри для математичного сподівання значення Упр інтервал довіри для окремого значення Упр, якщо Хпр=15N ( теоретична ймовірність 0,95). Вхідні данні Таблиця 9.2
де N порядковий номер вашого прізвища в журналі. 2. Занотувати отримані значення показників в таблицю:
3.Записати отримані економічні висновки у зошит _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ _____________________________________________________________________________________________________
4.Побудувати у зошиті графік лінійної регресії .
1. Запишіть у таблицю основні роки публікацій, прізвища дослідників та моделі економетрії
ТЕМА 10. ЛІНІЙНІ МОДЕЛІ МНОЖИННОЇ РЕГРЕСІЇ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 306. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
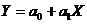 методом найменших квадратів, якщо задані вектори Х та У. Обчислить дисперсію залишків цієї моделі, середнє квадратичне відхилення, коефіцієнт кореляції, коефіцієнт еластичності.
методом найменших квадратів, якщо задані вектори Х та У. Обчислить дисперсію залишків цієї моделі, середнє квадратичне відхилення, коефіцієнт кореляції, коефіцієнт еластичності.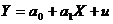 прямою лінією , де u - залишки (збурення моделі). Розрахункові значення (Ур) обчислимо, користуючись такою моделлю:
прямою лінією , де u - залишки (збурення моделі). Розрахункові значення (Ур) обчислимо, користуючись такою моделлю: (9.1)
(9.1)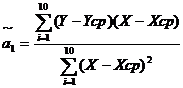 =1,7
=1,7
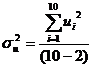 . Вона дорівнює 0,71 та середнє квадратичне відхилення . використовуючи формулу
. Вона дорівнює 0,71 та середнє квадратичне відхилення . використовуючи формулу 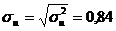

 =0,68 (9.3)
=0,68 (9.3)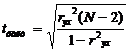
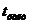 =17,047 , де r – вже обчислений нами раніше коефіцієнт кореляції.
=17,047 , де r – вже обчислений нами раніше коефіцієнт кореляції. де
де 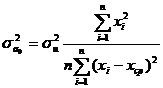
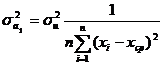 (9.4)
(9.4)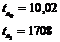

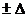 , (9.5)
, (9.5)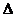 — гранична помилка прогнозу.
— гранична помилка прогнозу.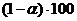 % має вигляд:
% має вигляд: . (9. 6)
. (9. 6)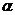 i k=N-1)ступенями вільності у випадку двосторонньої перевірки.
i k=N-1)ступенями вільності у випадку двосторонньої перевірки. (9.7)
(9.7) .
.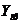 =30,84
=30,84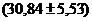
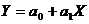 методом найменших квадратів, якщо задані вектори Х та У. Обчислить дисперсію залишків цієї моделі, середнє квадратичне відхилення, коефіцієнт кореляції, коефіцієнт еластичності. Перевірити модель на якість, в тому числі:
методом найменших квадратів, якщо задані вектори Х та У. Обчислить дисперсію залишків цієї моделі, середнє квадратичне відхилення, коефіцієнт кореляції, коефіцієнт еластичності. Перевірити модель на якість, в тому числі: