
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегрирование методом подстановки.Суть метода заключается в том, что мы вводим новую переменную, выражаем подынтегральную функцию через эту переменную, в результате приходим к табличному (или более простому) виду интеграла. Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами. Метод подстановки позволяет объяснить правило интегрирования Вводим новую переменную Подставляем полученные выражения в исходный интеграл: Если принять Подведение под знак дифференциала. Метод подведения под знак дифференциала основан на приведении подынтегрального выражения к виду
Интегрирование по частям. Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения
Определенный интеграл. Формула Ньютона – Лейбница. Приложения Определённый интеграл — аддитивный монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала). Формула Ньютона-Лейбница.  Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления. Приложения
Приложения производной к исследованию функции Монотонность функции. Переменную величину называют монотонной, если она изменяется только в одном направлении, т.е. либо только возрастает, либо только убывает. Очевидно, что движение точки х в сторону положительного направления оси абсцисс является монотонно возрастающим, а в противоположную сторону - монотонно убывающим. Функция у = f(х) называется монотонно возрастающей на интервале (а, b), если для любых х1, и х2, принадлежащих этому интервалу, из неравенства х2 > х1, следует неравенство f(х2) > f(x1) (рис. 3а). Функция у = f(х) называется монотонно убывающей на интервале (а, b), если для любых х1 и х2, принадлежащих этому интервалу, из неравенства х2 > х1, следует неравенство f(x2) < f(x1) (рис. 3б).
Рис. 3. Графики монотонно возрастающей и монотонно убывающей функций.
Экстремумы функции Пусть функция у = f(х) определена на отрезке [а;b]. Говорят, что функция у = f(х) имеет локальный максимум в точке х0 є [а;b], если существует окрестность точки х0, целиком содержащаяся в [а;b ] и такая, что для любого х, принадлежащего этой окрестности, выполняется неравенство f(х) < f(х0). Под окрестностью точки х0 понимают интервал длины 2e с центром в точке х0, т.е. (х0-e, х0+e), где e - произвольное положительное число Говорят, что функция у = f(х) имеет локальный минимум в точке х0 є[а;b], если существует окрестность точки х0, целиком содержащаяся в [а;b] и такая, что для любого х, принадлежащего этой окрестности, выполняется неравенство f(х) > f(х0). Достаточный признак экстремума функции. Критическая точка (внутренняя точка области определения функции, в которой производная этой функции равна нулю или не существует) является точкой экстремума функции, если в окрестности этой точки производная меняет знак, причем точкой максимума, если производная меняет знак с «+» на «-», и точкой минимума, если производная меняет знак с «-» на «+». Наибольшее (наименьшее) значение непрерывной функции у = f(х) на отрезке [а;b ]достигается либо в одной из критических точек, либо в одной из граничных точек данного отрезка. Выпуклость функции Говорят, что функция у = f(х) выпукла вверх в точке х0, если существует окрестность точки х0 такая, что для всех ее точек х касательная к графику функции в точке М0(х0, у0) лежит выше графика (рис. 4а). Говорят, что функция у = f(х) выпукла вниз в точке х0, если существует окрестность точки х0 такая, что для всех ее точек х касательная к графику функции а точке М0(х0; у0) лежит ниже графика (рис. 4б). Если на некотором промежутке (а;b) все касательные к графику функции у = f(х) лежат выше (соответственно ниже) самого графика, то на данном промежутке функция выпукла вверх (соответственно выпукла вниз).
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 255. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. , тогда
, тогда

 и вернуться к исходной переменной х, то получим
и вернуться к исходной переменной х, то получим
 . Далее применяется метод подстановки: вводится новая переменная
. Далее применяется метод подстановки: вводится новая переменная  и после нахождения первообразной для новой переменной, возвращаемся к исходной переменной, то есть
и после нахождения первообразной для новой переменной, возвращаемся к исходной переменной, то есть
 и последующем применении формулы
и последующем применении формулы  . Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.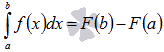 .
.




