
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Бесконечно – малые и бесконечно – большие функции и их связь
Непрерывность функции, точки разрыва. Основные теоремы о непрерывных функциях
Производная. Производная сложной функции. Производные высших порядков Производная функция - базовый элемент дифференциального исчисления, который является результатом применения какой-либо операции дифференцирования к исходной функции.
Название функции происходит от слова «произведенная», т.е. образованная от другой величины. Процесс определения производной какой-либо функции называется дифференцированием. Распространенный способ представления и определения - через теорию пределов, хотя она возникла позже дифференциального исчисления. Согласно этой теории производная - это предел отношения приращения функции к приращению аргумента, если такой предел существует, при условии, что аргумент стремится к нулю. Считается, что впервые термин «производная» употребил известный русский математик В.И.Висковатов.Чтобы найти производную функции f в точке x, необходимо определить значения этой функции в точке х и в точке x+ x, где x – приращение аргумента х. Найти приращение функции y = f(x+ x) – f(x). Записать производную через предел отношения f’ = lim(f(x+ x) – f(x))/ x, вычислить при x 0. Принято обозначать производную знаком апостроф «’» над дифференцируемой функцией. Один апостроф – первая производная, два – вторая, производная высшего порядка задается соответствующей цифрой, например, f^(n) – производная n-го порядка, где n – целое число 0. 
Производные высших порядков Пусть функция y = f(x) имеет производную y' = f'(x) во всех точках некоторой окрестности точки x0. Если функция f'(x) в свою очередь имеет в точке x0 производную y(2) Аналогично определяются и производные y(n) более высоких порядков n:
где для удобства считается, что y(0) = y. Примеры.
2. Если y = sin x, y' = cos x, y(2) = -sin x, y(3) = -cos x, y(4) = sin x. Заметив, что cos x = sin (x + y' = sin(x + Вообще,
Аналогично,
Неопределенный интеграл. Методы вычисления. Свойства Неопределенный интеграл Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается Выражение Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C. Свойства На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения. Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств: Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах. Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно; второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
Методы Непосредственное интегрирование. Основным методом нахождения первообразной функции является непосредственное интегрирование с использованием таблицы первообразных и свойств неопределенного интеграла. Все другие методы используются лишь для приведения исходного интеграла к табличному виду. Пример. Найдите множество первообразных функции Решение. Запишем функцию в виде Так как интеграл суммы функций равен сумме интегралов, то Числовой коэффициент можно вынести за знак интеграла: Первый из интегралов приведен к табличному виду, поэтому из таблицы первообразных для показательной функции имеем Для нахождения второго интеграла Следовательно, |
||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 327. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 непрерывна в точке
непрерывна в точке  , если
, если
 Графически же непрерывность функции y = f(x) означает непрерывность ее графика как линии на плоскости Oxy.
Имеет место следующая теорема (критерий непрерывности).
Теорема. Функция f(x),
Графически же непрерывность функции y = f(x) означает непрерывность ее графика как линии на плоскости Oxy.
Имеет место следующая теорема (критерий непрерывности).
Теорема. Функция f(x), 
 Как видно из рис. 13, в точке x0 разрыва функции f(x) ее левая "половина графика" не соединяется с "правой половиной", т.е. график "разорвался", а поэтому f(x) в точке x0 имеет разрыв.
Как видно из рис. 13, в точке x0 разрыва функции f(x) ее левая "половина графика" не соединяется с "правой половиной", т.е. график "разорвался", а поэтому f(x) в точке x0 имеет разрыв.




 , то она называется второй производной функции f в точке x0 и обозначается f"(x0) или f(2)(x0). Таким образом, опуская обозначения аргумента, имеем
, то она называется второй производной функции f в точке x0 и обозначается f"(x0) или f(2)(x0). Таким образом, опуская обозначения аргумента, имеем y"
y"  (y')'.
(y')'. /2), получим
/2), получим .
. называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

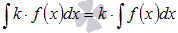 , где k – произвольная константа.
, где k – произвольная константа.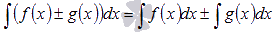

 .
. .
.

 .
. воспользуемся таблицей первообразных для степенной функции
воспользуемся таблицей первообразных для степенной функции  и правилом
и правилом  . То есть,
. То есть,  .
.
