
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные дифференциальные уравненияЗаданное дифференциальное уравнение называют линейным, если искомая функция и ее производная входят в уравнение в 1-ой степени:
Рассмотрим решение уравнения, записанного в виде Для функции Потребуем, чтобы функция Остаётся записать общее решение заданного уравнения Пример 1.4. Решить дифференциальное уравнение Решение. 1) Заданное уравнение линейное относительно 2) Применяя подстановку 3) Потребуем, чтобы 4) Теперь, интегрируя уравнение: 5) Записываем общее решение заданного уравнения 6) Используя начальные условия (задача Коши), находим Ответ. Замечание. В задании (1.4) используются линейные уравнения как относительно  Задание 1.4. Решить линейное дифференциальное уравнение и найти частное решение для заданных начальных условий.
Дифференциальное уравнение Бернулли Дифференциальное уравнение называют уравнением Бернулли, если оно имеет вид причём, в выражении (1.6) требуем, чтобы Известно, что при помощи подстановки Применив стандартный алгоритм решения линейного уравнения, находят функцию Пример 1.5. Решить дифференциальное уравнение Бернулли Решение. 1) Заданное дифференциальное уравнение есть уравнение Бернулли для случая 2) Считая 3) Полагая 4) Потребуем, чтобы 5) Теперь, интегрируя уравнение 6) Таким образом, Ответ. Задание 1.5. Решить уравнение Бернулли. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 185. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.  применением подстановки (метод Бернулли)
применением подстановки (метод Бернулли)  , где
, где 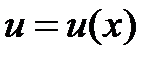 и
и  .
. вычислим производную
вычислим производную  и вместе с выражением
и вместе с выражением  подставим в заданное уравнение:
подставим в заданное уравнение: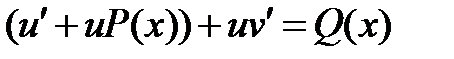 . (1.5)
. (1.5)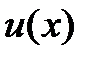 удовлетворяла условию
удовлетворяла условию  . Это уравнение с разделяющимися переменными. Нам нужно одно частное решение уравнения. Разделим переменные и проинтегрируем
. Это уравнение с разделяющимися переменными. Нам нужно одно частное решение уравнения. Разделим переменные и проинтегрируем 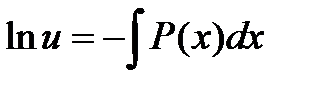 , или
, или  . Подставив
. Подставив  в (1.5), получим для нахождения
в (1.5), получим для нахождения  уравнение с разделяющимися переменными
уравнение с разделяющимися переменными  . Последнее легко интегрируется
. Последнее легко интегрируется  +
+  .
. =
=  , из которого для заданных начальных условий
, из которого для заданных начальных условий  выделяют частное решение.
выделяют частное решение. . Найти его частное решение при условии
. Найти его частное решение при условии  .
. и
и  , причём
, причём  и
и  .
. , перепишем заданное уравнение
, перепишем заданное уравнение  =
=  .
. . Это уравнение с разделяющимися переменными. Его частное решение
. Это уравнение с разделяющимися переменными. Его частное решение  =
=  , или
, или  =
=  .
.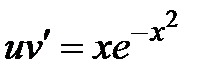 , получаем
, получаем 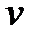 =
=  +
+  =
=  +
+  .
. =
=  ·
·  .
. =1 и записываем частное решение уравнения
=1 и записываем частное решение уравнения 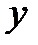 =
=  ·
·  .
.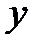 =
= 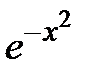 ·
·  – общее решение,
– общее решение,  =
=  ·
·  – частное решение.
– частное решение. , так и относительно
, так и относительно  . Для первого случая начальные условия представлены в виде:
. Для первого случая начальные условия представлены в виде:  , для второго случая в виде:
, для второго случая в виде:  .
. ,
, 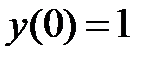 .
.
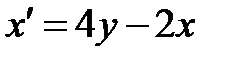 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
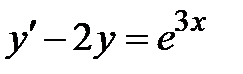 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
, 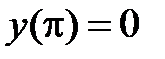 .
.
 ,
,  .
.
 ,
, 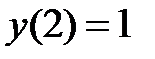 .
.
 ,
,  .
.
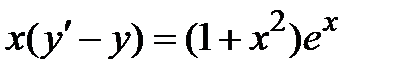 ,
,  .
.
 ,
, 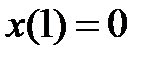 .
.
 ,
,  .
.
 ,
, 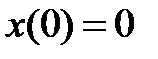 .
.
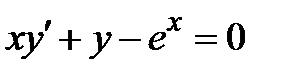 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 , (1.6)
, (1.6) не равнялось 0 или 1, так как при этих значениях уравнение (1.6) есть линейное уравнение. Заметим, что в случае
не равнялось 0 или 1, так как при этих значениях уравнение (1.6) есть линейное уравнение. Заметим, что в случае  >0 сразу выделяется одно из решений уравнения
>0 сразу выделяется одно из решений уравнения  =0.
=0. уравнение Бернулли превращается в линейное уравнение:
уравнение Бернулли превращается в линейное уравнение: 
 . Затем из равенства
. Затем из равенства 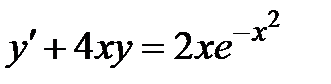 ∙
∙  .
. =
=  . Функция
. Функция 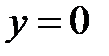 является его решением.
является его решением. , перепишем заданное уравнение в виде
, перепишем заданное уравнение в виде  . Применив подстановку
. Применив подстановку 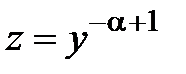 =
=  ,
, 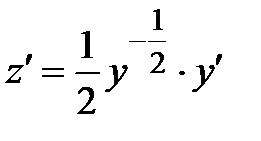 , получаем линейное дифференциальное уравнение
, получаем линейное дифференциальное уравнение 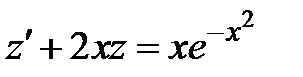 , где
, где  и
и  .
. , перепишем заданное уравнение
, перепишем заданное уравнение  =
=  .
. =
= 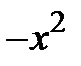 , или
, или 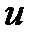 =
=  .
. , получаем
, получаем  =
=  +
+  =
=  +
+ 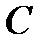 .
. =
=  ∙
∙  . Так как
. Так как  =
=  , получаем решение заданного уравнения
, получаем решение заданного уравнения 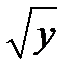 =
=  ∙
∙ 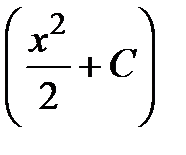 .
.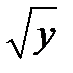 =
=  ·
·  ,
,  .
.