
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Другие характеристики центра группирования случайной величины
1. Среднегеометрическое случайной величины Х: G(Х) = eM(ln Х). Пусть Х – дискретная случайная величина, имеющая равномерное распределение.
2. Среднее гармоническое: Используется в экономике в индексных расчетах.
3. Медиана: Me(x) – квантиль xp, соответствующая вероятности p = 0,5. Точка хр, являющаяся решением уравнения F(xp) = р, называется квантилью распределения. Медиана используется в качестве характеристики среднего, если случайная величина измерена в порядковой шкале. 4.Мода: M0(x) – это значение случайной величины, соответствующей максимальной вероятности pi, если X – дискретная величина. Используется для оценки среднего величин, измеренных в номинальной шкале. Если Х – непрерывная случайная величина, то мода – точка локального максимума плотности распределения. Если плотность одномодального распределения непрерывной случайной величины симметрична относительно некоторой прямой х = а, то МХ = Ме(х) = М0(х) = а. Характеристики вариации случайной величины Характеристики вариации дают представления о степени отклонения случайной величины от центра группирования. Одной из характеристик вариации является среднее модуля отклонения случайной величины от своего математического ожидания. Для дискретной случайной величины
для непрерывных
Данную характеристику используют редко, так как выражение Определение 1.Дисперсией случайной величины X называют число, равное математическому ожиданию квадрата отклонения случайной величины от её математического ожидания:  Если Х – непрерывная, то Если Х – дискретная, то
Формулы (2) и (3) следуют из определения дисперсии и теорем 1 и 2 лекции 13. Часто пользуются другой формулой
Доказательство.
Определение 2. Средним квадратическим отклонением случайной величины называется квадратный корень из дисперсии: Пример1. Пусть Х – погрешность регистрации веса при взвешивании на весах с ценой деления 1 кг. Y – погрешность с ценой деления 2 кг. Найти DX, DY, σx, σy. Будем считать, что погрешности Х и Y равномерно распределены соответственно на интервалах (–0,5; 0,5) и (–1; 1), Тогда
По условию задачи один из весов вдвое точнее других, а дисперсии отличаются в четыре раза, в то время как среднеквадратические отклонения отличаются в два раза. Таким образом, среднеквадратическое отклонение может служить мерой точности приборов. Заметим, что единица измерения дисперсии – кг2, а единица измерения среднеквадратического отклонения – кг, т.е. среднеквадратическое отклонение измеряется в тех же величинах, что и исходная величина. Свойства дисперсии 1.Дисперсия постоянной C равна 0, DC = 0, С = const. Доказательство. DC = M(С – MC)2 = М(С – С) = 0.
2. D(CX) = С2DX. Доказательство. D(CX) = M(CX)2 – M2(CX) = C2MX2 – C2(MX)2 = C2(MX2 – M2X) = С2DX.
3. Если X и Y – независимые случайные величины, то
Доказательство.
4. Если Х1, Х2, … не зависимы, то Это свойство можно доказать методом индукции, используя свойство 3.
5. Доказательство. D(X – Y) = DX + D(–Y) = DX + (–1)2D(Y) = DX + D(Y).
6. Доказательство. D(C+X) = M(X+C–M(X+C))2 = M(X+C–MX–MC)2 = M(X+C–MX–C)2 = M(X–MX)2 = DX. Пусть Составим новую случайную величину То есть при n®¥ математическое ожидание среднего арифметического n независимых одинаково распределенных случайных величин остается неизменным, равным математическому ожиданию а, в то время как дисперсия стремится к нулю. Это свойство статистической устойчивости среднего арифметического лежит в основе закона больших чисел.
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 162. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , тогда
, тогда – среднее геометрическое.
– среднее геометрическое. .
. ,
, .
. задается разными функциями на разных участках. Этого недостатка лишены дисперсия и среднеквадратическое отклонение.
задается разными функциями на разных участках. Этого недостатка лишены дисперсия и среднеквадратическое отклонение. . (1)
. (1) . (2)
. (2)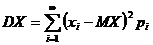 . (3)
. (3) . (4)
. (4)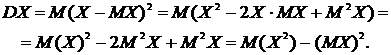
 .
. .
. Пользуясь выведенной формулой, получим –
Пользуясь выведенной формулой, получим – 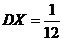 ;
;  ;
;  ;
;  .
.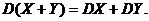

 .
. .
.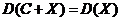
 – независимые случайные величины, причем
– независимые случайные величины, причем  ,
,  .
. , найдем математическое ожидание и дисперсию Y.
, найдем математическое ожидание и дисперсию Y. ;
; 
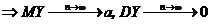 .
.