
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Інтегральна теорема Лапласа. ⇐ ПредыдущаяСтр 5 из 5 У схемі незалежних повторних випробувань
де Аналогічними міркуваннями для цієї схеми легко дістати формулу:
18.Вибірковий метод. Генеральна сукупність елементів. Вибірки та їх види в залежності від методів вибирання елементів. Вибірка властиво випадкова повторна і схема "неповернених куль". Незсуненість, ефективність та обгрунтованість як головні вимоги довибіркованих оцінок обраного параметра ознаки. Точкові вибіркові оцінки параметра. Довірчий інтервал вибіркової оцінки параметра. Оцінки якісних вибіркових ознак. Три типа задач вибіркового методу. Генеральною сукупністю в математичній статистиці називається множина однотипних об’єктів, кількісна чи якісна ознака яких підлягає вивченню. Підмножина об’єктів, дібраних у відповідний спосіб із генеральної сукупності, називається вибірковою сукупністю. Вважаємо, що ознака, яка вивчається, є випадковою величиною Х із функцією розподілу
 На підставі такого ряду можна побудувати статистичну функцію розподілу Точкові та інтервальні статистичні оцінки Статистична оцінка Точкова статистична оцінка називається ґрунтовною, якщо у разі необмеженого збільшення обсягу вибірки Довірчий інтервал для лінії регресії Ураховуючи те, що
Тоді
Звідси дістали:
має t-розподіл із
випливає
19.Перевірка правельності нульової гіпотези про нормальний закон розподілу ознаки генеральної сукупності Для перевірки правильності Н0 задається так званий рівень значущості a. a — це мала ймовірність, якою наперед задаються. Вона може набувати значення a = 0,005; 0,01; 0,001. В основу перевірки Н0 покладено принцип 1. Сформулювати Н0 й одночасно альтернативну гіпотезу Нa. 2. Вибрати статистичний критерій, який відповідав би сформульованій нульовій гіпотезі. 3. Залежно від змісту нульової та альтернативної гіпотез будується правобічна, лівобічна або двобічна критична область, а саме: нехай
4. Для побудови критичної області (лівобічної, правобічної чи двобічної) необхідно знайти критичні точки. За вибраним статистичним критерієм та рівнем значущості a знаходяться критичні точки. 5. За результатами вибірки обчислюється спостережуване значення критерію 6. Відхиляють чи приймають нульову гіпотезу на підставі таких міркувань: у разі, коли для двобічної критичної області або
Критерій узгодженості Пірсона.Критерій узгодженості Пірсона є випадковою величиною, що має розподіл
20.Функція розподілу
Функція розподілу має такі властивості:
Функції За допомогою функції розподілу можна подати ймовірність потрапляння випадкової точки у прямокутник, сторони якого паралельні осям координат:
Якщо розглядається система неперервних випадкових вели-чин, то для неї визначається щільність розподілу 1) 2) Імовірність потрапляння випадкової точки
Функція розподілу системи двох випадкових величин виражається через щільність розподілу:
Скориставшись властивостями функції розподілу системи неперервних величин, можна знайти щільності розподілу величин, які входять до цієї систем
21. Кореляційний момент. Коефіцієт кореляції та його властивості В теорії ймовірностей та математичній статистиці, кореляція (або коефіцієнт кореляції) є мірою залежності двох випадкових величин. При цьому, зміна однієї або кількох цих величин призводить до систематичної зміни іншої або інших величин. Математичною мірою кореляції двох випадкових величин слугує коефіцієнт кореляції. Кореляція може бути позитивною та негативною (можлива також ситуація відсутності статистичного зв’язку - наприклад, для незалежних випадкових величин). Від’ємна кореляція – кореляція, при якій збільшення однієї змінної пов’язане зі зменшенням іншої, при цьому коефіцієнт кореляції від’ємний. Додатна кореляція – кореляція, при якій збільшення однієї змінної пов’язане зі збільшенням іншої, при цьому коефіцієнт кореляції додатній. Нехай та — випадкові величини з математичним сподіванням μX та μY. Їх коефіцієнт кореляції позначається як і дорівнює:
де: σX,σY — стандартне відхилення величин Х та У .
Властивості
Якщо X та Y — незалежні, то коефіцієнт кореляції p(X Y) дорівнює 0. Зворотнє твердження невірне. Коефіцієнт кореляції може дорівнювати 0 навіть якщо Y є функцією від X.
Завжди виконується нерівність: .
Причому
22.функції одного випадкового аргументу Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргу-мента Х: Y = φ(X). Выясним, как найти закон распределения функции по известному закону распределения аргумента 1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Х соот-ветствуют различные значения Y. Тогда вероятности соответствующих значений Х и Y равны. 2) Если разным значениям Х могут соответствовать одинаковые значения Y, то вероятности значений аргумента, при которых функция принимает одно и то же значение, складываются. 3) Если Х – непрерывная случайная величина, Y = φ(X), φ(x) – монотонная и дифференцируемая функция, а ψ(у) – функция, обратная к φ(х), то плотность распределения g(y) случайно функции Y равна:
23. Функціональна, статистична та кореляційна залежності. Теорія лінійної кореляції. Основні положення кореляційного аналізу. Парна регресійна модель. Множинний регресійний аналіз Показником, що вимірює стохастичний зв’язок між змінними, є коефіцієнт кореляції, який свідчить з певною мірою ймовірності, наскільки зв’язок між змінними близький до строгої лінійної залежності. За наявності кореляційного зв’язку між змінними необхідно виявити його форму функціональної залежності (лінійна чи нелінійна), а саме:
Наведені можливі залежності між змінними X і Y називають функціями регресії. Форму зв’язку між змінними X і Y можна встановити, застосовуючи кореляційні поля, які зображені на рисунках Для двовимірного статистичного розподілу вибірки ознак (Х, Y) поняття статистичної залежності між ознаками Х та Y має таке визначення: статистичною залежністю Х від Y називають таку, за якої при зміні значень ознаки Y = yi змінюється умовний статистичний розподіл ознаки Х, статистичною залежністю ознаки Y від Х називають таку, за якої зі зміною значень ознаки X = xi змінюється умовний статистичний розподіл ознаки Y. Між ознаками Х та Y може існувати статистична залежність і за відсутності кореляційної. Але коли існує кореляційна залежність між ознаками Х та Y, то обов’язково між ними існуватиме і статистична залежність
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 201. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального.
Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального. де m — частота події А у n випробуваннях.
де m — частота події А у n випробуваннях. Результати вибірки розглядатимемо як послідовність незалежних однаково розподілених випадкових величин
Результати вибірки розглядатимемо як послідовність незалежних однаково розподілених випадкових величин  Закон розподілу для всіх
Закон розподілу для всіх  визначається функцією
визначається функцією  Результати вибірки — реалізації випадкових величин — позначатимемо відповідно через
Результати вибірки — реалізації випадкових величин — позначатимемо відповідно через 
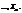 Розмістивши ці числа в порядку зростання і записавши частоти
Розмістивши ці числа в порядку зростання і записавши частоти  з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд:
з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд: Якщо
Якщо  , то статистична функція розподілу збігається д теоретичної функції розподілу.
, то статистична функція розподілу збігається д теоретичної функції розподілу. яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що
яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що  є випадковою величиною, точкова статистична оцінка може бути зміщеною і незміщеною: коли математичне сподівання цієї оцінки точно дорівнює оцінювальному параметру θ, а саме:
є випадковою величиною, точкова статистична оцінка може бути зміщеною і незміщеною: коли математичне сподівання цієї оцінки точно дорівнює оцінювальному параметру θ, а саме:  (1) то
(1) то  називається незміщеною; в противному разі, тобто коли
називається незміщеною; в противному разі, тобто коли  точкова статистична оцінка
точкова статистична оцінка  називається зміщеною відносно параметра генеральної сукупності θ. Різниця
називається зміщеною відносно параметра генеральної сукупності θ. Різниця  (3) називається зміщенням статистичної оцінки
(3) називається зміщенням статистичної оцінки  Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка
Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка  буде незміщеною й ефективною.
буде незміщеною й ефективною. Точкові статистичні оцінки
Точкові статистичні оцінки  часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою
часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою  та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме:
та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме:  (04) де δ є точністю оцінки. Оскільки
(04) де δ є точністю оцінки. Оскільки  є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю.
є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю. і
і  є випадковими величинами, то і лінійна функція регресії
є випадковими величинами, то і лінійна функція регресії  буде випадковою. Позначимо через
буде випадковою. Позначимо через  значення ознаки Y, обчислимо за формулою
значення ознаки Y, обчислимо за формулою .
. 




 .
. або
або .Випадкова величина
.Випадкова величина
 ступенями свободи. Ураховуючи можна побудувати довірчий інтервал для лінійної парної функції регресії із заданою надійністю γ, а саме:
ступенями свободи. Ураховуючи можна побудувати довірчий інтервал для лінійної парної функції регресії із заданою надійністю γ, а саме: .
. 
 , тобто ймовірність того, що статистичний критерій потрапляє в критичну область
, тобто ймовірність того, що статистичний критерій потрапляє в критичну область  , дорівнює малій імовірності a. Якщо ж виявиться, що
, дорівнює малій імовірності a. Якщо ж виявиться, що  а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу. Пропонується такий алгоритм перевірки правильності Н0:
а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу. Пропонується такий алгоритм перевірки правильності Н0: , тоді, якщо
, тоді, якщо , то вибирається правобічна критична область, якщо
, то вибирається правобічна критична область, якщо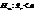 , то вибирається лівобічна критична область і коли
, то вибирається лівобічна критична область і коли , то вибирається двобічна критична область.
, то вибирається двобічна критична область. .
. , а це є малоймовірною випадковою подією,
, а це є малоймовірною випадковою подією,  і, незважаючи на це, вона відбулася, то в цьому разі Н0 відхиляється: для лівобічної критичної області
і, незважаючи на це, вона відбулася, то в цьому разі Н0 відхиляється: для лівобічної критичної області  ; для правобічної критичної області
; для правобічної критичної області 

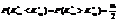 , ураховуючи ту обставину, що критичні точки
, ураховуючи ту обставину, що критичні точки  і
і  симетрично розташовані відносно нуля.
симетрично розташовані відносно нуля. , який визначається за формулою
, який визначається за формулою  і має k = q – m – 1 ступенів свободи, де q — число часткових інтервалів інтервального статистичного розподілу вибірки; m — число параметрів, якими визначається закон розподілу ймовірностей генеральної сукупності згідно з нульовою гіпотезою. Так, наприклад, для закону Пуассона, який характеризується одним параметром l, m = 1, для нормального закону m = 2, оскільки цей закон визначається двома параметрами
і має k = q – m – 1 ступенів свободи, де q — число часткових інтервалів інтервального статистичного розподілу вибірки; m — число параметрів, якими визначається закон розподілу ймовірностей генеральної сукупності згідно з нульовою гіпотезою. Так, наприклад, для закону Пуассона, який характеризується одним параметром l, m = 1, для нормального закону m = 2, оскільки цей закон визначається двома параметрами  i s. Якщо
i s. Якщо  (усі емпіричні частоти збігаються з теоретичними), то
(усі емпіричні частоти збігаються з теоретичними), то  , у противному разі
, у противному разі  . Визначивши при заданому рівні значущості a і числу ступенів свободи критичну точку
. Визначивши при заданому рівні значущості a і числу ступенів свободи критичну точку  , за таблицею (додаток 8) будується правобічна критична область. Якщо виявиться, що спостережуване значення критерію
, за таблицею (додаток 8) будується правобічна критична область. Якщо виявиться, що спостережуване значення критерію 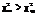 , то Н0 про закон розподілу ознаки генеральної сукупності відхиляється. У противному разі
, то Н0 про закон розподілу ознаки генеральної сукупності відхиляється. У противному разі  Н0 приймається.
Н0 приймається.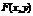 системи двох випадкових величин визначає ймовірність спільного настання двох подій:
системи двох випадкових величин визначає ймовірність спільного настання двох подій: 
 Геометрично функцію розподілу можна інтерпретувати як імовірність потрапляння випадкової точки в нескінченний прямокутник із вершиною
Геометрично функцію розподілу можна інтерпретувати як імовірність потрапляння випадкової точки в нескінченний прямокутник із вершиною  обмежений згори і праворуч
обмежений згори і праворуч




 визначають закони розподілу для випадкових величин
визначають закони розподілу для випадкових величин  які входять до системи.
які входять до системи.

 При цьому
При цьому  має такі властивості:
має такі властивості:

 у довільну область D подається формулою:
у довільну область D подається формулою:

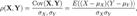
 — коваріація величин Х та ,У
— коваріація величин Х та ,У
 , тоді і лише тоді, коли
, тоді і лише тоді, коли  , де a та b — сталі.
, де a та b — сталі. ;
;  ;
; 