
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Математичне сподівання ДВВ та його властивості. довести (на вибір) 3 з нихМатематичним сподіванням, або середнім значенням, МХ випадкової величини, називається ряд 1) 2) 3) 4) Дисперсія ДВВ та її властивості. Довести (на вибір) 3 з них. Середнє квадратичне відхилення Дисперсія (позначається через
Основні властивості дисперсії: 1) 2) 3) Середнє квадратичне відхилення (позначається літерою s) є квадратним коренем із дисперсії. Якщо від випадкової величини віднімемо її математичне сподівання, то дістанемо центровану випадкову величину, математичне сподівання якої дорівнює нулю. Ділення випадкової величини на її середнє квадратичне відхилення називається нормуванням цієї випадкової величини. Випадкова величина 8. Незалежні повторні випробування -НВП. НВП як випробування, проведені за схемою "повернених куль". Виведення формул для математичного сподівання, дисперсії та середнього квадратичного відхилення частоти та відносної частоти в схемі незалежних повторних випробувань Математичним сподіванням, або середнім значенням, МХ випадкової величини, називається ряд 5) 6) 7)  Дисперсія (позначається через
Основні властивості дисперсії: 4) 5) 6) Середнє квадратичне відхилення (позначається літерою s) є квадратним коренем із дисперсії. Якщо від випадкової величини віднімемо її математичне сподівання, то дістанемо центровану випадкову величину, математичне сподівання якої дорівнює нулю. Ділення випадкової величини на її середнє квадратичне відхилення називається нормуванням цієї випадкової величини. Випадкова величина Формула Бернуллі. Біноміальний закон розподілу ймовірностей (закон Бернуллі). найімовірніша частота (мода) настання події. Локальна теорема Лапласа. Формула Пуассона. Закон рідкісних подій (закон Пуассона) Формула Бернуллі.Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так: |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 183. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (для дискретних випадкових величин) і інтеграл
(для дискретних випадкових величин) і інтеграл  (для неперервних випадкових величин), якщо вони абсолютно збіжні. Математичне сподівання має такі властивості:
(для неперервних випадкових величин), якщо вони абсолютно збіжні. Математичне сподівання має такі властивості: (С — стала);
(С — стала);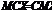 ;
;
 якщо Х і Y — незалежні випадкові величини.
якщо Х і Y — незалежні випадкові величини. ) випадкової величини Х визначається за формулою:
) випадкової величини Х визначається за формулою:


 якщо випадкові величини незалежні.
якщо випадкові величини незалежні. має нульове математичне сподівання й одиничну дисперсію.
має нульове математичне сподівання й одиничну дисперсію. Формула застосовується, якщо
Формула застосовується, якщо 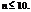 Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так:
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так:  Закон Бернуллі.Імовірності в цьому законі визначаються за формулою
Закон Бернуллі.Імовірності в цьому законі визначаються за формулою 
 m = 0,1,2, …, n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р. Частота настання події А має біноміальний закон розподілу. Імовірнісна твірна:
m = 0,1,2, …, n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р. Частота настання події А має біноміальний закон розподілу. Імовірнісна твірна:  Мода дискретної величини (МО) — це таке її значення, імовірність якого найбільша.Локальна теорема Лапласа. Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:
Мода дискретної величини (МО) — це таке її значення, імовірність якого найбільша.Локальна теорема Лапласа. Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю: 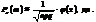
 Локальна теорема Лапласа дає змогу обчислювати ймовірності
Локальна теорема Лапласа дає змогу обчислювати ймовірності  , якщо n > 10 i p > 0,1.Формула Пуассона малоймовірних випадкових подій.
, якщо n > 10 i p > 0,1.Формула Пуассона малоймовірних випадкових подій.  Точність асимптотичних формул для великих значень n- числа повторних незалежних експериментів за схемою Бернуллі – знижується з наближенням p- до нуля .Тому при n → R,p- 0 за умови np=a=const імовірність появи випадкової події m раз (0<=m <=n),обчислюється за такою асимптотичною формулою: Якщо в кожному з n незалежних повторних випробувань
Точність асимптотичних формул для великих значень n- числа повторних незалежних експериментів за схемою Бернуллі – знижується з наближенням p- до нуля .Тому при n → R,p- 0 за умови np=a=const імовірність появи випадкової події m раз (0<=m <=n),обчислюється за такою асимптотичною формулою: Якщо в кожному з n незалежних повторних випробувань  , а n велике, то
, а n велике, то  Закон розподілу ПуассонаДискретна випадкова величина має розподіл Пуассона, якщо вона набуває зліченної множини значень
Закон розподілу ПуассонаДискретна випадкова величина має розподіл Пуассона, якщо вона набуває зліченної множини значень  з імовірностями
з імовірностями  Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. У таблицях для відповідних значень а наведено ймовірності
Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. У таблицях для відповідних значень а наведено ймовірності  Якщо у схемі незалежних повторних випробувань n велике і р або 1 – р прямують до нуля, то біноміальний розподіл апроксимується розподілом Пуассона, коли
Якщо у схемі незалежних повторних випробувань n велике і р або 1 – р прямують до нуля, то біноміальний розподіл апроксимується розподілом Пуассона, коли  Ймовірна твірна
Ймовірна твірна 