
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
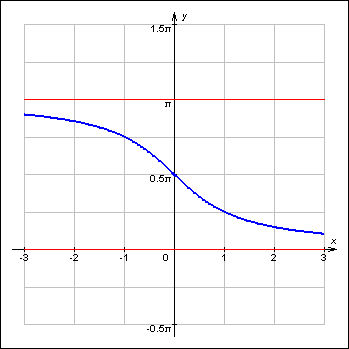
Обратные тригонометрические функции, графики, свойстваФункция Арксинусомчисла х, где 2. Функция Арккосинусомчисла х, где 3. Функция 4. Функция Функции Некоторые важные тождества:
Метрические соотношения в окружности. Свойства хорд. Свойства секущих и касательных к окружности. Измерение углов, связанных с окружностью Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки, называемой центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом окружности.  Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется ее диаметром. Диаметр равен двум радиусам, а радиус равен половине диаметра. Если на окружности взять две точки, то они разобьют окружность на две части, каждая из которых называется дугой окружности, а данные точки — концами этих дуг. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности. Часть плоскости, ограниченная окружностью, называется кругом. Кругом с центром О и радиусом R называется фигура, которая состоит из всех точек плоскости, удаленных от точки О не больше, чем на расстояние R. Свойства хорд
Дано: CD — диаметр окружности О, АВ — хорда окружности О, М = AB∩CD, CD ┴ АВ. Доказать: AM = MB. Доказательство. Треугольник АОВ равнобедренный (OA = OB) и ОМ — его высота, а значит, ОМ — медиана, т. е. AM= MB. n
Опр..Угол, вершина которого лежитв центре окружности, называется центральным углом. Если две хорды АВ и KL пересекаются в точке М, то справедливо равенство: АМ*МВ=КМ*ML
Д-во: Равенство углов АОВ и COD следует из равенства треугольников АОВ и COD (по трем сторонам).Эта теорема может быть сформулирована и таким образом: равные хорды видны из центра окружности под равными углами, и наоборот, под равными углами из центра окружности видны равные хорды.n Опр. Градусной мерой дуги окружности называется градусная мера центрального угла, который соответствует этой дуге. Две дуги одной окружности наз. равными, если их градусные меры равны. Т4. Вписанный угол измеряется половиной дуги, на которую он опирается. Следствие. Вписанные углы, опирающиеся на одну и ту же дугу, равны. Следствие. Вписанный угол, опирающийся на полуокружность (т.е. на диаметр), прямой. Опр. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Опр. Всякая прямая, имеющая с окружностью две общие тонки, называется секущей этой окружности.
Т6. (признак касательной). Прямая, проходящая через точку окружности и перпендикулярная ее радиусу, проведенному в эту точку, касается окружности. Опр. Пусть из точки А проведены две касательные р и т к окружности с центром в точке О, которые касаются окружности в точках Р и М соответственно (см. рис.).
(OA — общая). Таким образом, АР = AM и Т8. Дуги, заключенные между параллельными хордами окружности, равны. Док-во: Равенство дуг АС и BD непосредственно следует из равенства углов ABC и BCD. (см. рис. Справа ------>------>------>------>------>------>------>) n
Эту теорему можно сформулировать еще и так: если касательная параллельна хорде, то точка касания делит дугу, стягиваемую хордой, пополам.n
Т11. Угол, вершина которого лежит вне круга и стороны пересекают окружность, измеряется полуразностью дуг, отсекаемых сторонами угла и заключенных внутри него. Т12. Угол, образованный двумя касательными к окружности, равен полуразности большей и меньшей дуг, на которые окружность разбивается точками касания. |
||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 696. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
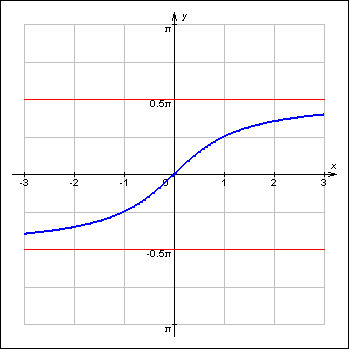
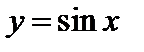 на отрезке
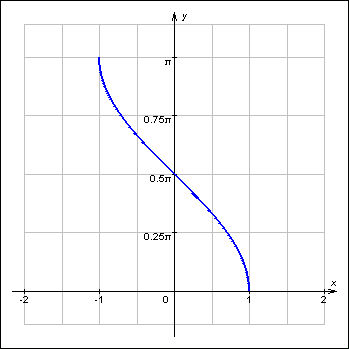
на отрезке 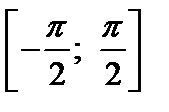 имеет обратную функцию, которая называется арксинусом
имеет обратную функцию, которая называется арксинусом называется такое число у,
называется такое число у, 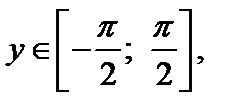 синус которого равен числу х. Обозначают:
синус которого равен числу х. Обозначают: 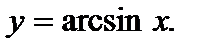 Таким образом,
Таким образом, 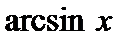 – это угол у, измеренный в радианах, такой, что
– это угол у, измеренный в радианах, такой, что  Для любого
Для любого 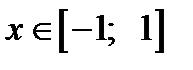 имеем
имеем 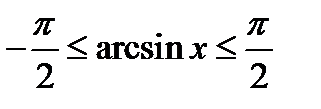 ,
, 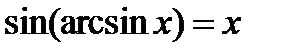 .
.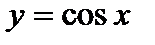 на отрезке
на отрезке 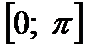 имеет обратную функцию, которая называется арккосинусом.
имеет обратную функцию, которая называется арккосинусом.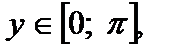 косинус которого равен числу х. Обозначают:
косинус которого равен числу х. Обозначают: 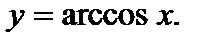 Таким образом,
Таким образом,  – это угол у, измеренный в радианах, такой, что
– это угол у, измеренный в радианах, такой, что 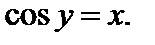 Для любого
Для любого 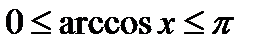 ,
,  .
.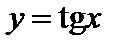 на промежутке
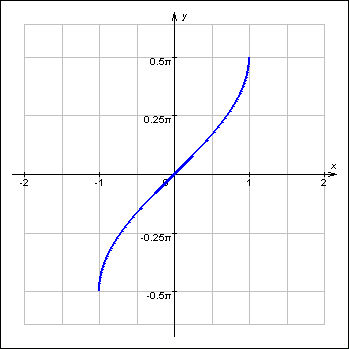
на промежутке 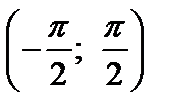 имеет обратную функцию, которая называется арктангенсом. Арктангенсомчисла х,
имеет обратную функцию, которая называется арктангенсом. Арктангенсомчисла х,  называется такое число у,
называется такое число у, 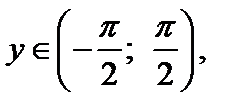 тангенс которого равен числу х. Обозначают:
тангенс которого равен числу х. Обозначают: 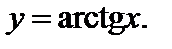 Таким образом,
Таким образом, 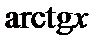 – это угол у, измеренный в радианах, такой, что
– это угол у, измеренный в радианах, такой, что 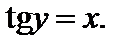 Для любого
Для любого 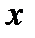 имеем
имеем 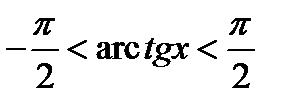 ,
, 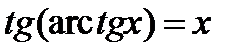 .
. на промежутке
на промежутке 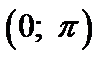 имеет обратную функцию, которая называется арккотангенсом. Арккотангенсомчисла х,
имеет обратную функцию, которая называется арккотангенсом. Арккотангенсомчисла х,  называется число у,
называется число у, 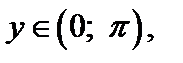 котангенс которого равен числу х. Обозначается:
котангенс которого равен числу х. Обозначается: 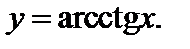 Таким образом,
Таким образом,  – это угол у, измеренный в радианах, такой, что
– это угол у, измеренный в радианах, такой, что 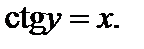 Для любого
Для любого 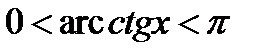 ,
, 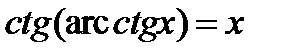 .
.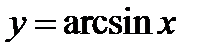 ,
, 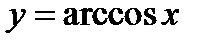 ,
, 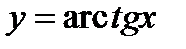 ,
, 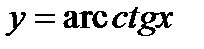 называют обратными тригонометрическими функциями или аркфункциями.
называют обратными тригонометрическими функциями или аркфункциями.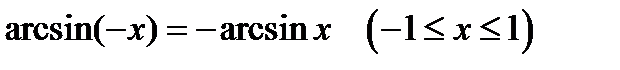 ,
,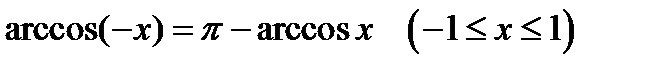
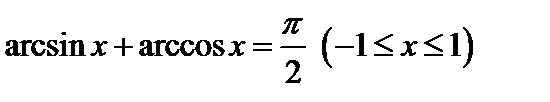 ,
,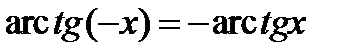 ,
, 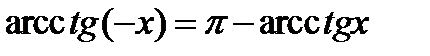 ,
,  .
.

 OND =
OND = 
 Т5. (свойство касательной). Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Т5. (свойство касательной). Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Т9. Дуги, заключенные между касательной к окружности и параллельной ей хордой и этой окружности, равны. Доказательство. ОМ ┴т , т.к. т — касательная к окр. О в точке М. Значит, ОМ ┴АВ, так как т || АВ.
Т9. Дуги, заключенные между касательной к окружности и параллельной ей хордой и этой окружности, равны. Доказательство. ОМ ┴т , т.к. т — касательная к окр. О в точке М. Значит, ОМ ┴АВ, так как т || АВ. Тогда в равнобедренном треугольнике АОВ ON— биссектриса, где N = ОМ ∩АВ, т. е.
Тогда в равнобедренном треугольнике АОВ ON— биссектриса, где N = ОМ ∩АВ, т. е.  AM =
AM = 
 Т10. Угол между двумя пересекающимися хордами измеряется полусуммой дуг этой окружности, одна из которых заключена между его сторонами, а другая — между их продолжениями.
Т10. Угол между двумя пересекающимися хордами измеряется полусуммой дуг этой окружности, одна из которых заключена между его сторонами, а другая — между их продолжениями.