
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон Ома для неоднородного участка цепи . ⇐ ПредыдущаяСтр 7 из 7
Сопротивление проводников. Электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь поперечного сечения проводника:
2. Закон полного тока. Закон полного тока это закон, связывающий циркуляцию вектора напряженности магнитного поля и ток. Циркуляция вектора напряженности магнитного поля по контуру равна алгебраической сумме токов, охватываемых этим контуром.
Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток протоивоположного направления считается отрицательным.
Применение закона для расчета магнитного поля тороида.
где
Если R >>Rвитка, то R ≈r и H = n?. Билет 20. 1. Работа по перемещению проводника с током в магнитном поле.
На проводник с током в МП действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки), то под действием  1. Для определения этой работы рассмотрим проводник длиной lс током I (он может свободно перемещаться), помещенный в однородное м.п. перпендикулярное к плоскости контура. Направление силы определяется по правилу левой руки, а значение – по закону Ампера Под действием этой силы проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая МП равна:
– площадь, пересекаемая проводником при его перемещении в магнитном поле. Поток вектора магнитной индукции, пронизывающей эту площадь равен:
Таким образом, работа по перемещению проводника с током в МП, равна произведению силы тока на магнитный поток, пересеченный движущимся проводником:
Полученная формула справедлива и для произвольного направления вектора 2. Вычислим работу по перемещению замкнутого контура с постоянным током в м.п. (произвольное движение). Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение
Контур М мысленно разобьем на два соединенных своими концами проводника: АВС и СDА. Работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура в м.п., равна алгебраической сумме работ по перемещению проводников АВС и СDА (dA1 и dA2), то есть:
Силы приложенные к участку CDA контура образуют с направлением перемещения острые углы, поэтому совершаемая ими работа dA2>0. Эта работа, согласно формулам равна:
где dФ0 – поток, который пересекает проводник CDA при движении; dФ2 – поток, пронизывающий контур в его конечном положении. Силы, действующие на участок АВС контура, образуют с направлением перемещения тупые углы, следовательно dA1 <0. Проводник АВС пересекает при своем движении поток dФ0 сквозь поверхность и dФ1 – поток, пронизывающий контур в начальном положении. Следовательно:
Подставляя выражения для dA1 и dA2 в формулу (37.5), получим выражение для элементарной работы:
– изменение магнитного потока сквозь площадь, ограниченную контуром с током. Таким образом,
Проинтегрировав это выражение, определим работу, совершаемую силами Ампера при конечном произвольном перемещении контура в м.п.:
2. Энергия и плотность энергии магнитного поля. Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна где Sl = V — объем соленоида. |
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 298. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 - знаки "+" или "-" выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем.
- знаки "+" или "-" выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем.

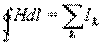


 Тороид – тор, с намотанными на него витками проволоки. В отличие от соленоида, у которого магнитное поле имеется как внутри, так и снаружи, у тороида магнитное поле полностью сосредоточено внутри витков, т.е. нет рассеивания энергии магнитного поля.
Тороид – тор, с намотанными на него витками проволоки. В отличие от соленоида, у которого магнитное поле имеется как внутри, так и снаружи, у тороида магнитное поле полностью сосредоточено внутри витков, т.е. нет рассеивания энергии магнитного поля.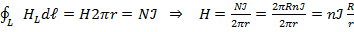 ,
,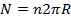 .
. – магнитное поле тороида.
– магнитное поле тороида.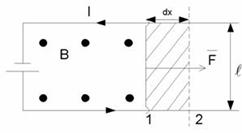
 он будет в МП перемещаться. Следовательно, МП совершает работу по перемещению проводника с током.
он будет в МП перемещаться. Следовательно, МП совершает работу по перемещению проводника с током. .
. ,
,
 ,
,
 .
.
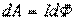 .
.
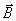 .
. . Направление тока в контуре – по часовой стрелке и м.п. перпендикулярно плоскости чертежа.
. Направление тока в контуре – по часовой стрелке и м.п. перпендикулярно плоскости чертежа.
 .
.
 ,
,
 .
.
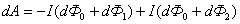 ,
,
 ,
,
 ,
,
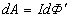 .
.
 .
.
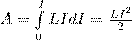
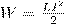 (1)
(1)  Так как I=Bl/(μ0μN) и В=μ0μH , то
Так как I=Bl/(μ0μN) и В=μ0μH , то  (2)
(2)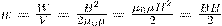 (3)
(3)