
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Правило сложение скоростей.Рассмотрим движение материальной точки в системе Кʹ, которая движется относительно К со скоростью V. Определим скорость это же точки в системе К Vx=dx/dt Vxʹ= dxʹ/dt Vy=dy/dt Vyʹ=dyʹ/dt Vz=dz/dt Vzʹ=dzʹ/dt Согласно преобразованиям Лоренца: dx= dt= Проведя соответствующие преобразования, получаем релятивистский закон сложения скоростей в СТО K→Kʹ Kʹ→K Vxʹ= Vyʹ= Vzʹ= Вопрос 2. Поток вектора электрического смещения. Электрическое смещение-векторная величина, равная сумме вектора напряженности электрического поля и вектора поляризации Единица элемента смещения- кулон на метр в квадрате(Кл/м2)
Теорема Гаусса для электрического поля в диэлектрике. Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов.
Где Dn-проекция вектора D на нормаль n к площади dS
Билет 14. Вопрос 1 Преобразования Лоренца. Рассмотрим две инерциальные системы отсчета: K(x,y,z) и Kʹ(xʹ,yʹ,zʹ), движущуюся относительно К (вдоль оси х) со скоростью v = const Пусть в начальный момент времени t = t' = 0, когда начала координат О и О' совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одна и та же и равна с. Поэтому если за время t в системе K сигнал дойдет до некоторой точки А (см. рис. 61), пройдя расстояние x=ct, то в системе К' координата светового импульса в момент достижения точки А  Так как х'≠х (система К' перемещается по отношению к системе К), то tʹʹ≠t, т. е. отсчет времени в системах К и К' различен — отсчет времени имеет относительный характер
K Kʹ
x xʹ
z zʹ Переход из одной инерциальной системы отсчета к другой: К→Кʹ Kʹ→K xʹ=x-Vt x=xʹ yʹ=y y=yʹ zʹ=z z=zʹ tʹ=t t=tʹ преобразования Лоренца: K→Kʹ Kʹ→K xʹ= yʹ=y y=yʹ где β= zʹ=z z=zʹ tʹ= Следствия из преобразований Лоренца 1)Одновременность событий в разных системах отсчета. Если события в системе К происходят в одной точке {х1 = х2) и являются одновременными (t1 = t2), то эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета. 2)Длительность событий в разных системах отсчета. τʹ= Длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся. 3)Длина тел в разных системах отсчета. Длина стержня, измеренная в системе относительности, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой стержень покоится. l0ʹ= Cокращение длины тем больше, чем больше скорость движения. Линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится. Вопрос 2. Магнитное поле в веществе. Магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Можно записать, что вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля B0 и поля микротоков В' где, Намагниченность. Намагниченность-векторная величина, характеризующая магнитное состояние макроскопического физического тела.
Где Связь векторов J, B и H. Вектор магнитной индукции для соленоида из одного витка N=1 B=µ0 Если
B=µ0
Билет № 15 1)Релятивистская механика - раздел частной теории относительности, посвященный изучению движения материальных тел под действием приложенных к ним сил. При изучении движения элементарных частиц было замечено, что обычные классические формулы динамики и законы сохранения энергии и импульса не выполняются в случае движения частиц с околосветовыми скоростями. Вместо классического импульса p=mv записывается в виде Масса m, входящая в выражение для импульса, есть фундаментальная характеристика частицы, не зависящая от выбора инерциальной системы отсчета, а, следовательно, и от скорости ее движения. Основной закон релятивистской динамики материальной точки записывается так же, как и второй закон Ньютона: Следовательно,
Полная энергия и импульс частицы определяются соотношениями E = mc2γ, p = γmv = vE/c2. Полная энергия импульс и масса связаны соотношением E2 - p2c2 = m2c4. 2) Закон Био́ - Савáра - Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Элемент тока длины dl создает поле с магнитной индукцией или в векторной форме: Это и есть закон Био–Савара–Лапласа, полученный экспериментально. Как видно из рисунка, вектор магнитной индукции направлен перпендикулярно плоскости, проходящей через и точку, в которой вычисляется поле. Здесь I – ток; – вектор, совпадающий с элементарным участком тока и направленный в ту сторону, куда течет ток; – радиус-вектор, проведенный от элемента тока в точку, в которой мы определяем ; r – модуль радиус-вектора; k – коэффициент пропорциональности, зависящий от системы единиц. Направление связано с направлением «правилом буравчика»: направление вращения головки винта дает направление , поступательное движение винта соответствует направлению тока в элементе. Таким образом, закон Био–Савара–Лапласа устанавливает величину и направление вектора в произвольной точке магнитного поля, созданного проводником с током I. Модуль вектора определяется соотношением: где α – угол между и ; k – коэффициент пропорциональности, зависящий от системы единиц. Физика. Билет 16 1)В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов. Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой: Для параллельного соединения конденсаторов будет справедлива следующая формула: Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и -q, то согласно формуле напряжение между обкладками конденсатора равно В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0. Среднее значение напряжения в процессе разрядки равно Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь: Следовательно, потенциальная энергия Wp конденсатора электроемкостью С, заряженного до напряжения U, равна Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. 2) Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная: Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб). Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю: Это теорема Остроградского-Гаусса для магнитного поля. Она свидетельствует о том, что в природе не существует магнитных зарядов – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции. Билет 17 1) Постоянный электрический ток- ток, который с течением времени не изменяется по величине и заряда I=q/t
А мы знаем, что
это запись закона Ома в дифференциальной форме.
Билет 18 1) постоянный электрический ток(17 билет)
Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности
где S - поперечное сечение проводника,
с учетом закона Ома в дифференциальной форме Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля. Билет 19. Электродвижущая сила. ЭДС — энергетическая характеристика источника. Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду: Измеряется в вольтах (В).
|
||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 309. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 dy=dyʹ dz=dzʹ
dy=dyʹ dz=dzʹ
 Vx=
Vx= 
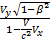 Vy=
Vy= 
 Vz=
Vz= 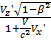

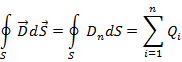
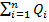 -алгебраическая сумма свободных зарядов, охватываемых замкнутой поверхностью S
-алгебраическая сумма свободных зарядов, охватываемых замкнутой поверхностью S
 y yʹ
y yʹ




 O Oʹ V A
O Oʹ V A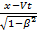 x=
x= 

 t=
t= 
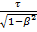
 β=V/c
β=V/c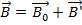
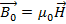 (H-вектор напряженности, µ0-магнитная постоянная)
(H-вектор напряженности, µ0-магнитная постоянная)
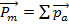 - магнитный момент магнетика, представляющий собой векторную величину суммы магнитного момента отдельных молекул.
- магнитный момент магнетика, представляющий собой векторную величину суммы магнитного момента отдельных молекул. , где Iʹ-сила молекулярного тока, l-длина цилиндра
, где Iʹ-сила молекулярного тока, l-длина цилиндра магнитный момент магнетика объема V, то намагниченность магнетика:
магнитный момент магнетика объема V, то намагниченность магнетика:

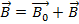

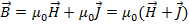


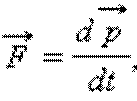

 .
. .
.

 .
. .
.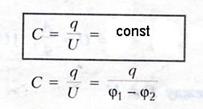 .
.

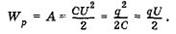 .
. .
.
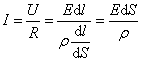
 или
или  . Отсюда можно записать
. Отсюда можно записать


 , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника
, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника
 - его длина. Используя (1.13) и соотношение
- его длина. Используя (1.13) и соотношение  , получим
, получим
 - плотность тока, а
- плотность тока, а 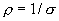 , тогда
, тогда 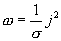
 , окончательно получаем
, окончательно получаем  (17.14)
(17.14)