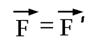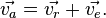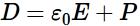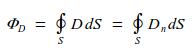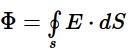Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вопрос 2. Энергия и плотность энергии магнитного поля.Энергия магнитного ноля, связанного с контуром W= Плотность энергии (энергия единицы объема) вычисляют как Билет 6 Принцип относительности Галилея. Во всех системах координат, движущихся равномерно и прямолинейно относительно системы неподвижных звезд и друг относительно друга, все механические явления протекают, совершено одинаково. Такие системы координат называются инерциальными. В настоящее время принцип относительности Галилея с большой точностью экспериментально доказан для механических и электромагнитных явлений. Преобразования Галилея. Пусть система идвижутся со скоростью. Отсчет времениt начинаем с момента совпадения начала координат. Тогда координаты произвольной точки Р в этих системах:
t – время перемещения. В Ньютоновской механике предполагаем, что время во всех системах отсчета течет одинаково. Таким образом, в перемещающейся системе вдоль y характер движения может быть произвольным. Совокупность четырех уравнений – преобразования Галилея. Продифференцируем первое уравнение по времени, учтя, что
Следовательно:
Дифференцируем 2 и 3 уравнения:
то есть
то есть
Иначе: Это уравнение – формула преобразования скорости частицы от системы Дифференцирование по времени последнего уравнения:
Ускорение частицы относительно систем К и
Законы механики одинаковы во всех инерциальных системах отсчета – Принцип относительности Галилея. Величины, которые имеют одно и то же числовое значение, во всех системах отсчета, называются инвариантными: промежуток времени, масса, ускорение, сила, длина предмета.  Эйнштейн вводит в физику принцип постоянства скорости света. Скорость света в вакууме не зависит от движения источников света и, следовательно, одинакова во всех инерциальных системах отсчета. Впервые скорость света была измерена в 1676г. 300000км\с. Справедливость постоянной c=const была доказана Майкельсоном и Морли в 1887 году. Итак, с инварианта во всех инерциальных системах координат , считается так же на данном этапе исследований Вселенной, что с = max. Существование предельной скорости приводит к тому, что понятие одновременности становится относительным. Например, в середине поезда зажигается световой сигнал. Если наблюдатель находится в центре поезда, то он отметит одновременное достижение света хвоста и головы поезда. Дежурный на станции отметит, что сигнал достиг хвоста раньше, чем головы. Скорость передачи информации – скорость света – конечна, поэтому путь, проделанный световым сигналом от конца поезда до дежурного меньше пути, проделанного световым сигналом от головы до дежурного, поэтому и время будет различно, хотя очень незначительно. Значительность этого эффекта будет проявляться при скоростях движения объектов, близких к скорости света. Значит, время течет по-разному в различных системах отсчета, но почувствовать это реально можно только при движении объектов со скоростями, близких к С. 1)3) Теорема о сложении скоростей В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей: 2)1) Вектор электрического смещения. Электрическое смещение — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации (Кл/м2).
Поток вектора D сквозь поверхность:
Теорема Остроградского − Гаусса: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 324. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
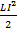
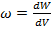 или для однородного поля
или для однородного поля 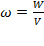
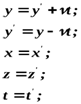
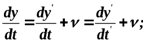
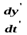 - проекция скорости частицы
- проекция скорости частицы  в системе
в системе 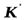 на ось
на ось 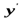 .
.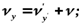
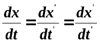 ;
;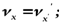
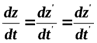 ;
;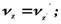
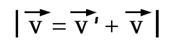
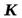 к
к 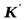 .
.
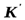 одинаковы.
одинаковы.