
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнение Бернулли для потока реальной жидкости
Пусть поток реальной жидкости, обладающей вязкостью, движется в русле, ограниченном неподвижными стенками. При этом вследствие трения между слоями жидкости существенно возрастает неравномерность распределения скоростей по сечению потока (рисунок 3.5), а также возникают потери энергии на трение при перемещении жидкости от одного сечения к другому. Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием, что тоже требует затрат энергии. Поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоления сопротивлений, и, следовательно, уменьшается вдоль потока. Получим уравнение Бернулли для потока реальной жидкости, основываясь на том, что оно является законом сохранения энергии для движущейся жидкости. Вывод этого уравнения проведем в два этапа. На первом этапе учтем неравномерность распределения скоростей по сечению потока, а на втором учтем и потери энергии. При выводе будем считать, что в пределах выбранных сечений гидростатический напор остается постоянным:
На первом этапе определим формулу для вычисления мощности N потока реальной жидкости в его сечении. Вычисление этого параметра затруднено тем, что из-за перераспределения скоростей (см. рисунок 3.5),разные слои жидкости несут различное количество энергии. Для определения мощности N в сечении (например, в сечении 1— 1 на рисунке 3.5) выберем струйку жидкости бесконечно малой поперечной площади dS, в пределах которой скорость жидкости будем считать постоянной, равной υ. Тогда полный напор (или полная удельная энергия) в сечении струйки 
Мощность струйки dN всечении площадью dS равнапроизведению удельной энергии Н и веса жидкости, которую проносит поток через это сечение в единицу времени, т.е. элементарного весового расхода dQG. Тогда с учетом (3.6) и (3.1) получим математическую зависимость для мощности струйки:
Мощность всего потока в сечении найдем, просуммировав мощности всех элементарных струек, т. е. вычислив интеграл по площади S от выражения (3.9):
После математических преобразований зависимость для мощности потока реальной жидкости принимает следующий вид:
где α – безразмерный коэффициент, определяемый по формуле
Этот коэффициент, называемый коэффициентом Кориолиса, учитывает неравномерность распределения скорости жидкости в сечении реального потока. Если числитель и знаменатель в формуле (3.11) умножить на ρ/2, то станет очевидно, что коэффициент α есть отношение действительной кинетической энергии реального потока в данном сечении к кинетической энергии того же потока в том же сечении, но посчитанной по средней скорости жидкости в данном сечении. В этом заключается физический смысл коэффициента Кориолиса. Алгебраическое выражение, ограниченное скобками в (3.10), принято называть средним значением полного напора в сечении реального потока, т.е.
Средний напор Нср широко используется в практических расчетах, так как является важнейшим параметром, характеризующим механическую энергию (или мощность) потока реальной жидкости. Для подтверждения этого решим уравнение (3.10) относительно Hср с учетом (3.12). Тогда получим
Из анализа зависимости (3.13) следует, что при постоянном расходе Q средний напор Hср пропорционален мощности N и в пределах данного потока однозначно определяет эту мощность. Поэтому средний напор Hср, вычисляемый с учетом неравномерности распределения скоростей в сечении по формуле (3.12), в дальнейшем будем использовать в качестве основного параметра, характеризующего механическую энергию потока реальной жидкости. Учтем теперь потери энергии, возникающие при движении жидкости. В реальных потоках из-за этих потерь среднее значение полного напора в конечном сечении всегда меньше, чем в начальном сечении, т.е. H ср1 > H ср2. Поэтому при записи уравнения баланса энергий (средних напоров) в его правую часть добавляют слагаемое
или с учетом (3.12)
Уравнение (3.14) носит название уравнения Бернулли для потока реальной жидкости. Сравним уравнение Бернулли для струйки идеальной жидкости (3.6) и уравнение для потока реальной жидкости (3.14). Из этого сравнения следует, что в последнем уравнении дополнительно присутствуют α и При равномерном распределении скоростей по сечению потока α = 1(поток идеальной жидкости). В потоках реальной жидкости коэффициент Кориолиса в большинстве случаев лежит в пределах 1 < α < 2. Суммарная потеря полного напора Местные потери hм - это потери в так называемых местных гидравлических сопротивлениях, к которым относятся поворот, сужение или расширение потока, а также различные гидравлические устройства (вентили, жиклеры и т.д.). Потери в большинстве этих сопротивлений вызваны вихреобразованием. Как показывает практика, они пропорциональны квадрату скорости жидкости, а для оценки их величины используется формула Вейсбаха
где ζ — безразмерный коэффициент, определяющий потери в данном местном сопротивлении; υср — средняя скорость в трубопроводе, в котором установлено местное сопротивление. Второй вид гидравлических потерь - потери на трение по длине hтр — это потери, которые имеют место в длинных прямых трубах постоянного сечения. Потери на трение по длине вызваны как внутренним трением в жидкости, так и трением о стенки трубы. Эти потери пропорциональны длине трубы l и обратно пропорциональны ее диаметру d. Они имеют достаточно сложную зависимость от средней скорости жидкости (это будет рассмотрено позднее), но во всех случаях для их оценки может быть использована универсальная для гидравлики формула Дарси
где λ — безразмерный коэффициент потерь на трение по длине, который принято называть коэффициентом Дарси. Следует отметить, что определение потерь энергии при расчете гидравлических систем является одной из наиболее важных проблем гидравлики.
6. Примеры использования уравнения Бернулли в технике
Уравнение Бернулли широко применяется в технике, как для выполнения гидравлических расчетов, так и для решения ряда практических задач. Одной из таких задач является измерение скорости и расхода жидкости. Рассмотрим некоторые устройства для измерения расхода и скорости жидкости.
Запишем для сечений 1—1 и 2—2 потока уравнение Бернулли и уравнение расхода (считая распределение скоростей равномерным):
где hм — потеря напора между сечениями 1-1 и 2-2. Учитывая, что
найдем из этой системы уравнений одну из скоростей, например
отсюда объемный расход
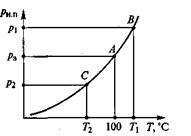
или где С – величина, постоянная для данного расходомера. Зная величину С и наблюдая за показанием пьезометра, можно найти расход в трубопроводе для любого момента временя по формуле (3.18). Константу С можно определить теоретически, но точнее ее можно найти экспериментально, т. е. в результате градуирования расходомера. Связь между ΔН и Q получается параболической, а если по оси абсцисс откладывать расход во второй степени, то график этой зависимости будет представлять собой прямую. Очень часто вместо пары пьезометров для измерения перепада давления в расходомере применяют дифференциальный ртутный манометр. Учитывая, что над ртутью в трубках находится та же жидкость плотностью ρ, можно записать
 Трубка полного напора (или трубка Пито) служит для измерения скорости, например, в трубе (рисунок 3.7). Если установить в этом потоке трубку, изогнутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость υ частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке. Трубка полного напора (или трубка Пито) служит для измерения скорости, например, в трубе (рисунок 3.7). Если установить в этом потоке трубку, изогнутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость υ частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.
На этом же принципе основано измерение скорости полета самолета. На рисунке 3.7 показана схема самолетной скоростной трубки (насадка) для измерения малых по сравнению со скоростью запуска скоростей полета. Запишем уравнение Бернулли для струйки, которая набегает на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где υ = 0), получаем
Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р2 ≈ р0, следовательно из предыдущего имеем
Другим важным случаем практического использования уравнения Бернулли является создание топливно-воздушной смеси для двигателей внутреннего сгорания с помощью карбюратора и эжектора. Карбюраторпоршневых двигателей внутреннего сгорания служит для подсоса бензина и смешения его с потоком воздуха (рисунок 3.9). Поток воздуха; засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха. Найдем соотношение между массовыми расходами бензина Qб и воздуха Qв при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2-2) ζв и жиклера ζж (сопротивлением бензотрубки пренебрегаем).
откуда
Учитывая, что массовые расходы
Таким образом обеспечивается постоянство соотношения расходов бензина и воздуха. Однако следует иметь в виду приближенный характер данного решения
|
||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 394. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
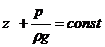 .
.  Это справедливо для сечений с параллельно струйным течением жидкости, т. е. когда эти сечения являются плоскими. Поэтому уравнение, которое будет получено ниже, может использоваться только для плоских или близких к ним сечений.
Это справедливо для сечений с параллельно струйным течением жидкости, т. е. когда эти сечения являются плоскими. Поэтому уравнение, которое будет получено ниже, может использоваться только для плоских или близких к ним сечений. .
.  .
. 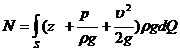 .
.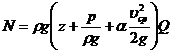 ,
,  .
. 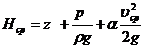 .
.  .
.  , учитывающее потери удельной энергии. Тогда уравнение баланса принимает вид
, учитывающее потери удельной энергии. Тогда уравнение баланса принимает вид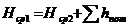 ,
, ,
,  ,
,  ,
, 
 Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока - дросселирование (рисунок 3.6). Расходомер состоит из двух участков - плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в суженном месте возрастает, а давление падает. Возникает разность (перепад) давлений, которая измеряется двумя пьезометрами или дифференциальным U-образным манометром и определенным образом связана с расходом. Найдем эту связь. Допустим в сечении 1-1 потока непосредственно перед сужением скорость потопа равна υ1, давление р1, площадь сечении S1, а в сечении 2-2, т. е. в самом узком месте потока, соответственно υ2, р2, S2. Разность показаний пьезометров, присоединенных к указанным сечениям ΔН.
Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока - дросселирование (рисунок 3.6). Расходомер состоит из двух участков - плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в суженном месте возрастает, а давление падает. Возникает разность (перепад) давлений, которая измеряется двумя пьезометрами или дифференциальным U-образным манометром и определенным образом связана с расходом. Найдем эту связь. Допустим в сечении 1-1 потока непосредственно перед сужением скорость потопа равна υ1, давление р1, площадь сечении S1, а в сечении 2-2, т. е. в самом узком месте потока, соответственно υ2, р2, S2. Разность показаний пьезометров, присоединенных к указанным сечениям ΔН.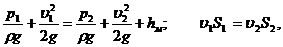
 и
и 
 ,
,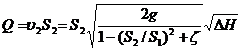
 ,
, 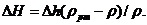

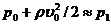
 .
. Записав уравнение Бернулли для потока воздуха (сечение 0-0 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z1 = z2 и α = 1):
Записав уравнение Бернулли для потока воздуха (сечение 0-0 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z1 = z2 и α = 1):

 и
и  , получим
, получим
 Струйный насос (эжектор) состоит из плавно сходящегося насадка А (рисунок 3.10), осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В. Вследствие увеличения скорости потока давление в струе на выходе из насадка и по всей камере В и значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно, в камере В давление обычно меньше атмосферного, т.е. возникает разрешение (вакуум). Под действием разрежения жидкость из нижнего резервуары всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков.
Струйный насос (эжектор) состоит из плавно сходящегося насадка А (рисунок 3.10), осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В. Вследствие увеличения скорости потока давление в струе на выходе из насадка и по всей камере В и значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно, в камере В давление обычно меньше атмосферного, т.е. возникает разрешение (вакуум). Под действием разрежения жидкость из нижнего резервуары всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков.