
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сила давления на плоскую стенку
При определении силы, действующей со стороны жидкости на плоскую стенку, рассмотрим общий случай, когда стенка наклонена к горизонту под углом α, а на свободную поверхность жидкости действует давление р0 (рисунок 2.5). Вычислим силу давления F, действующую на некоторый участок рассматриваемой стенки площадью S. Ось Ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось Оу — перпендикулярно к этой линии в плоскости стенки. Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS: dF = p dS = (pо + ρ gh) dS = pо dS + ρ g h d S, где ро — давление на свободной поверхности; h — глубина расположения площадки dS. Для определения полной силы F проинтегрируем полученное выражение по всей площади S:
где у — координата площадки dS. Последний интеграл представляет собой статический момент площади S относительно оси Ох и равсн произведению этой площади на координату ее центра тяжести (точка С), то есть
Следовательно
здесь hс — глубина расположения центра тяжести площади S. Или окончательно получим
т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление рС в центре тяжести этой площади. В частном случае, когда давление ро является атмосферным и действует также с другой стороны стенки, сила F избыточного давления жидкости на плоскую стенку равна лишь силе Fж давления от веса жидкости, т. е. 
В общем случае давление ро может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку будем рассматривать как сумму двух сил: Fо от внешнего давления pо и силы Fж от веса жидкости, то есть F = F0 + Fж = (pо + рС) S. Найдем точки приложения этих сил, называемых центрами давления. Так как внешнее давление ро передается всем точкам площади S одинаково, то его равнодействующая Fо будет приложена в центре тяжести площади S. Для нахождения точки приложения силы давления Fж от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющих сил, т. е. где yD — координата точки приложения силы Fж Выражая Fж и dFж через уС и у и определяя yD, получаем
где Учитывая, что где Jxо — момент инерции площади S относительно центральной оси, параллельной Ох, находим
Таким образом, точка приложения силы Fж расположена ниже центра тяжести площади стенки; расстояние между ними
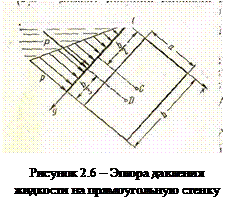
Если давление ро равно атмосферному, то точка D и будет центром давления. При ро выше атмосферного центр давления находят по правилам механики как точку приложения равнодействующей двух сил: Fо и Fж, чем больше первая сила по сравнению со второй, тем, очевидно, центр давления ближе к центру тяжести площади S. В частном случае, когда стенка имеет форму прямоугольника размерами ахb (рисунок 2.6) и одна из его сторон а лежит на свободной поверхности с атмосферным давлением, центр давления D находится на расстоянии b/3 от нижней стороны.
Сила давления на криволинейные стенки. Плавание тел
Рассмотрим силу, действующую на криволинейную цилиндрическую стенку, которая погружена в жидкость так, что ее образующие параллельны свободной поверхности жидкости (рисунок 2.7). Такие стенки распространены на практике. В этом случае задача может быть сведена к определению равнодействующей силы, лежащей в вертикальной плоскости, перпендикулярной образующим цилиндрической поверхности. Определение этой силы сводится к определению ее вертикальной и горизонтальной составляющих.
Для определения силы F в первом случае (см. рисунок 2.7, а) выделим объем жидкости, ограниченный поверхностью АВ и вертикальными плоскостями, проходящими через границы выбранного участка. На рисунке 2.7, а эти плоскости отображены линиями AL и ВК. Рассмотрим условия равновесия выделенного объема в вертикальном и горизонтальном направлениях, из которых найдем вертикальную FB и горизонтальную FГ составляющие силы F. Навыделенный объем жидкости в вертикальном направлении, кроме силы FB, действуют его вес G и сила давления на свободную поверхность, равная произведению давления р0 на площадь горизонтальной проекции поверхности АВ, обозначаемую Sr. Тогда из условия равновесия найдем вертикальную составляющую FВ = po S Г + G. При рассмотрении условия равновесия в горизонтальном направлении будем считать, что силы, действующие на поверхности ЕК и AL, взаимно уравновешены. Следовательно, на выделенный объем жидкости в горизонтальном направлении, кроме искомой силы F1, действует только сила давления на площадь вертикальной проекции поверхности АВ, обозначаемую SB. Ее найдем по формуле (2.4): FГ = pC SB = (p0+hc ρ g) SВ, где hc - глубина погружения центра тяжести поверхности АВ, SB — площадь поверхности BE. Определив по формулам (2.7) и (2.8) вертикальную FB и горизонтальную FГ составляющие силы F, найдем ее численное значение по зависимости
Зависимости (2.7) - (2.9) получены для случая с расположением жидкости над криволинейной поверхностью. Очевидно, что при расположении жидкости снизу относительно стенки (см. рисунок 2.7, б) давления в соответствующих точках будут точно такими, как и в первом случае. Поэтому и силы, действующие на стенку (полная сила и ее вертикальная и горизонтальная составляющие), будут такими же по значению. Но направления этих сил будут противоположными, так как жидкость действует на стенку с обратной стороны. Таким образом, формулы будут справедливы и для этого случая. При этом в формулу (2.7) входит та же величина G, т.е. вес жидкости, которая заняла бы объем ABKL (выделен на рис. 2.7, б). Полученные зависимости справедливы для цилиндрической поверхности, которая погружена в жидкость так, что ее образующие параллельны свободной поверхности. Аналогичным образом могут быть получены формулы для произвольной криволинейной поверхности. Их отличие будет в том, что полная сила F будет равна векторной сумме не двух составляющих сил (как в предыдущем случае), а трех. Причем одна из этих составляющих будет вертикальной, а две — горизонтальными и взаимно-перпендикулярными. Определение положения точки приложения силы F, действующей на криволинейную стенку, является весьма сложной задачей, которая решается с использованием графических или численных (компьютерных) методов. Определение положения точки приложения силы F, действующей на поверхность вращения (например, цилиндрическую), упрощается, так как в этом случае линия действия силы F проходит через ось вращения поверхности.
При рассмотрении сил, действующих на тело, условно разделим его замкнутой линией MNOR на две части: верхнюю и нижнюю. Причем линия разделения MNOR проведена так, что ее проекция и проекция тела на свободную поверхность жидкости (т. е. вертикально вверх) полностью совпадают. Обозначим вес жидкости, расположенной над телом, G0 (на рисунке 2.8, а выделена штриховкой), а вес жидкости, вытесненной телом, — G, т.е. это вес жидкости, которая заняла бы объем погруженного тела (на рис. 2.8, а выделен затемнением). Вертикальную силу (см. рисунок 2.8, а),действующую на нижнюю поверхность тела, определим с использованием формулы (2.7): FB1 = p0 SГ + G0 + G, где SГ — площадь горизонтальной проекции тела на свободную поверхность жидкости. Таким же образом найдем вертикальную силу (см. рисунок 2.8, а), действующую на верхнюю часть тела: FB2 = p0 SГ + G0 . Их равнодействующая сила Fa, направленная вверх, будет равна алгебраической сумме этих сил и с учетом (2.10) и (2.11) определяется по формуле
Силу Fa принято называть архимедовой силой, а полученную для ее определения зависимость — законом Архимеда, согласно которому на тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу жидкости, вытесненной телом. Точкой приложения этой силы является геометрический центр тела, который называется центром водоизмещения. Он может не совпадать с центром тяжести тела. Эти центры совпадают, если тело состоит из однородного и равномерно распределенного вещества. Плавающее тело будет находиться в устойчивом равновесии, когда центр водоизмещения располагается выше центра тяжести тела, и они лежат на одной вертикальной прямой (см. рисунок 2.8, б).
Относительный покой жидкости
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью. Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляется новая — сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках. Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются. Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения tga = а/g.
p = p0 + l ρ j. Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
где z0 — высота расположения точки свободной поверхности относительно дна сосуда; h0 — высота жидкости на оси вращения. Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
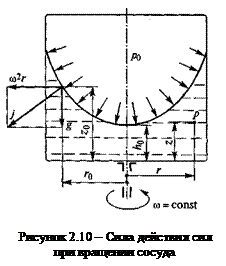
На практике часто встречается другой частный случай — вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве. 4 КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ
|
||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 389. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 До сих пор рассматривались давления, действующие в жидкости. Однако более важное практическое значение имеют силы, возникающие от действия жидкости на различные стенки.
До сих пор рассматривались давления, действующие в жидкости. Однако более важное практическое значение имеют силы, возникающие от действия жидкости на различные стенки.
 ,
,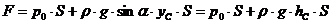 ,
,
 .
. ,
, ,
, — момент инерции площади S относительно оси Ох.
— момент инерции площади S относительно оси Ох. ,
, .
. 
 .
. В пределах цилиндрической поверхности (см. рисунок 2.7) выделим участок АВ и найдем силу F, действующую на этот участок при условии, что на свободной поверхности жидкости существует давление р0. Причем определим эту силу для двух случаев: жидкость расположена над цилиндрической поверхностью (см. рисунок 2.7, а) и под ней (см. рис. 2.7, б). При определении силы, действующей на стенку, будем учитывать, что со стороны стенки на жидкость действует такая же сила, но в противоположном направлении.
В пределах цилиндрической поверхности (см. рисунок 2.7) выделим участок АВ и найдем силу F, действующую на этот участок при условии, что на свободной поверхности жидкости существует давление р0. Причем определим эту силу для двух случаев: жидкость расположена над цилиндрической поверхностью (см. рисунок 2.7, а) и под ней (см. рис. 2.7, б). При определении силы, действующей на стенку, будем учитывать, что со стороны стенки на жидкость действует такая же сила, но в противоположном направлении.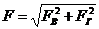 .
.  Важной задачей при решении некоторых практических вопросов является определение силы, выталкивающей тело, погруженное в жидкость. На рисунке 2.8, а изображено тело произвольной формы, погруженное в жидкость. Рассмотрим силы, действующие на это тело в вертикальном направлении.
Важной задачей при решении некоторых практических вопросов является определение силы, выталкивающей тело, погруженное в жидкость. На рисунке 2.8, а изображено тело произвольной формы, погруженное в жидкость. Рассмотрим силы, действующие на это тело в вертикальном направлении.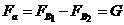 .
.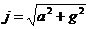
 Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость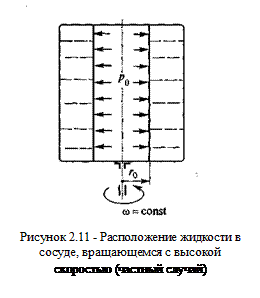

 ,
, .
.  .
.