
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Статистические характеристики выборки при количественной изменчивости признакаК количественным относят признаки, которые могут быть охарактеризованы количественно: урожай с делянки, число, высота и масса растений, содержание белка и клейковины в зерне, т. е. все, что имеет массу, размер, объем и т. п. Различают два вида количественной изменчивости: непрерывную и прерывистую или дискретную. В первом случае значения признака выражены мерами объема, длины, массы и т. д., во втором различия между единицами наблюдения выражаются целыми числами, между которыми нет, и не может быть переходов, например, число зерен в колосе и число завязей, семян, листьев, побегов на растениях, число самих растений и т. д. Ход анализа вариационных рядов количественной изменчивости зависит от объема выборки – малого или большого. Как для малых, так и для больших выборок вычисляют следующие основные статистические характеристики: среднюю арифметическую ( Средняя арифметическая (
где Х – отдельные значения признака в выборке; n –объем выборки.
Дисперсия (S2).Дисперсии характеризуют величину изменения вариационных рядов и специфику варьирования. Дисперсию вычисляют по формуле:
Стандартное отклонение (S).Как и дисперсия,стандартное отклонение выражается в тех же единицах измерения, что и характеризуемый им признак, и служит основной мерой вариации, рассеяния изучаемого признака. Чем сильнее варьирует показатель, тем больше числовое значение стандартного отклонения. В расчетах оно является более удобной характеристикой, чем дисперсия. Стандартное отклонение представляет собой корень квадратный из дисперсии, и вычисляют его по формуле: 
Коэффициент вариации (V). Дисперсия и стандартное отклонение не-пригодны, когда в опытах сравнивают изменчивость признаков, выраженных разными единицами измерения (масса урожая, т; число плодов, шт.; длина побегов, см; площадь листьев, см2; и др.). В этих случаях пользуются коэффициентом вариации. Коэффициент вариации V– это отношение стандартного отклонения (S) к средней арифметической (Х), выраженное в процентах:
Принято считать варьирование незначительным, если коэффициент вариации находится в пределах 10 %, средним, если он равен 10-20 %, и значительным, если он превышает 20 % Ошибка выборочной средней (
Относительная ошибка выборочной средней (
Чем меньше относительная ошибка, тем выше точность средней арифметической. Точность принято считать высокой при S Х % <3 % , средней – при S Х % = 3-6 % и низкой – при S Х % > 6-7 %.
Доверительный интервал средней арифметической определяется с95 % уровнем вероятности. Теоретическое значение t (табличное значение) для 5 % уровня значимости (t05) при степени свободы n-1 (7):
где
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 446. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
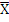 ), дисперсию (S2), стандартное отклонение (S), ошибку средней арифметической (
), дисперсию (S2), стандартное отклонение (S), ошибку средней арифметической ( 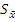 ), коэффициент вариации (V), относительную ошибку средней арифметической (
), коэффициент вариации (V), относительную ошибку средней арифметической ( 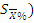 . В конце анализа дают интервальную оценку средней арифметической.
. В конце анализа дают интервальную оценку средней арифметической.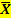 ). Средняя арифметическая является основной статистической характеристикой вариационного ряда, все остальные лишь объясняют ее. Среднюю арифметическую вычисляют по формуле:
). Средняя арифметическая является основной статистической характеристикой вариационного ряда, все остальные лишь объясняют ее. Среднюю арифметическую вычисляют по формуле: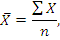
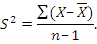
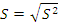
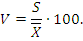
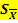 ).Средние арифметические имею ошибки, которые возникают в результате неполной представительности выборки. Эти ошибки свойственны только выборочному методу исследования, их числовое значение зависит как от степени изменчивости изучаемого признака, так и от объема выборки. Ошибку выборочной средней вычисляют по формуле:
).Средние арифметические имею ошибки, которые возникают в результате неполной представительности выборки. Эти ошибки свойственны только выборочному методу исследования, их числовое значение зависит как от степени изменчивости изучаемого признака, так и от объема выборки. Ошибку выборочной средней вычисляют по формуле: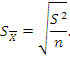
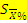 )–это отношение ошибки выборочной средней к соответствующей средней арифметической, выраженное в процентах (6):
)–это отношение ошибки выборочной средней к соответствующей средней арифметической, выраженное в процентах (6):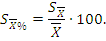
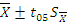
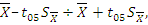
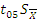 – доверительная граница.
– доверительная граница.