
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение систем линейных уравненийСистема линейных алгебраических уравнений
представима в матричной форме Ax = b, (9) где A – матрица коэффициентов при неизвестных системы (матрица левой части системы),
b – столбец свободных слагаемых,
Известно, что система линейных алгебраических уравнений имеет решение, если ее определитель отличен от 0, т. е. если Умножим обе части матричного уравнения Ax = b на обратную матрицу коэффициентов при неизвестных системы A-1 слева: С учетом того, что вектор-столбец решений системы принимает вид: Реализация данного алгоритма в Mathcad включает: · формирование матрицы A коэффициентов при неизвестных и вектора-столбца b свободных слагаемых системы уравнений; · нахождение решения системы по формуле · вывод (отображение в документе) значений вектора решений системы уравнений Кроме того, Mathcad имеет встроенную функцию lsolve(A, b), возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы уравнений и столбец свободных слагаемых. Порядок решения аналогичен рассмотренному, но вместо вычисления по формуле  Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы. Решение системы линейных уравнений можно найти с помощью блоков Given…Find, Given…Minerr. Пример 8. Решить систему линейных уравнений Сделать проверку полученного решения. Решение. 1 Использование блока Given…Find. Задайте всем неизвестным, входящим в систему уравнений, начальные приближения, например,
Наберите ключевое слово Given и уравнения системы, разделяя левую и правую часть каждого из них логическим знаком равенства =, который вводится нажатием комбинации клавишCtrl =. Завершите вычислительный блок вводом оператора присваивания X := Find(x, y, z) (15) Mathcad-код и результаты решения системы уравнений в виде вектора, состоящего из трех элементов, представлены в следующем фрагменте документа Mathcad:
Сделайте проверку результатов решения системы уравнений, подставив полученные значения неизвестных в выражения для левых частей уравнений системы и завершив набор каждого такого выражения нажатием клавиши =: Видно, что полученные значения выражений левых частей уравнений системы совпадают c константами их правых частей, т. е. найденные значения неизвестных действительно являются решением системы уравнений. В данном примере системная переменная ORIGIN = 1. 2 Использование блока Given…Minerr. Порядок решения системы этим способом аналогичен порядку использования блока Given…Find. Результаты решения вместе с результатами проверки представлены в следующем фрагменте документа:
3 Решение системы линейных уравнений матричным способом. Создайте матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого наберите A := и вызовите диалоговое окно создания массивов (Ctrl M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполните шаблон матрицы как показано ниже:
Задайте вектор b правых частей системы уравнений, введя сначала b :=, затем вставив шаблон матрицы (Ctrl M) с количеством строк (Rows) и столбцов (Columns) равным 3 и 1 соответственно и заполнив его поля ввода необходимыми числами:
Представьте расчетную формулу матричного метода оператором присваивания и выведите найденные значения вектора-решения:
Найдите решение системы уравнений с помощью функции lsolve:
Получите решение системы уравнений посредством функции rref:
Полученная путем объединения матрицы при неизвестных системы и столбца правых частей уравнений матрица AR называется расширенной матрицей системы уравнений. Проверка правильности решения системы уравнений X, полученного матричным способом, заключается в вычислении произведения
с вектором-столбцом b. |
|||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 347. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 ;
; .
. . (10)
. (10) . (11)
. (11) , (12)
, (12) . (13)
. (13) ;
; .
. .
. (14)
(14)






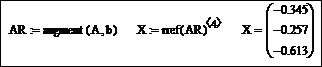
 и сравнении найденного вектора
и сравнении найденного вектора