
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема о взаимности возможных работСтр 1 из 13Следующая ⇒ Лекция пятнадцатая Теоремы взаимности строительной механики 15.1. Теорема о взаимности возможных работ 15.2. Теорема о взаимности перемещений 15.3. Теорема о взаимности реакций 15.4. Теорема о взаимности реакций и перемещений 15.5. Вопросы для самопроверки 15.6. Рекомендуемая литература Теорема о взаимности возможных работ Рассмотрим два состояния какого-либо сооружения, например балки на двух опорах (рис. 15.1,а). В состоянии i на эту балку действует обобщённая сила Fi, а состоянии j – обобщённая сила Fj. Обобщённые силы Fi и Fj в упомянутых состояниях прикладываются статическим способом. На рис. 15.1,а показаны действительные (Dii, Djj) и возможные (Dij, Dji) перемещения по направлению обобщённых сил (о статическом способе приложения нагрузки и о смысле понятий "действительное перемещение", "возможное перемещение" см. в п. 10.2 десятой лекции второй части "Лекций по строительной механике стержневых систем").
Вычислим работу обобщённых сил Fi и Fj от их совместного воздействия. Сначала статическим способом приложим обобщённую силу Fi, которая на перемещении Dii будет совершать действительную работу Wext,ii (рис. 15.1,б). После окончательного формирования обобщённой силы Fi статическим способом приложим обобщённую силу Fj. Балка получит дополнительные деформации и перемещения: Dij – возможное перемещение в направлении обобщённой силы Fi от действия обобщённой силы Fj, Djj – действительное перемещение в направлении обобщённой силы Fj от её же воздействия (рис. 15.1,б внизу). Постоянная по величине обобщённая сила Fi совершает возможную работу Wext,ij на перемещении Dij, а статически приложенная сила Fj – действительную работу Wext,jj на перемещении Djj. Суммарная работа 
В п. 10.2 десятой лекции получены зависимости для вычисления действительной и возможной работы внешних обобщённых сил Fi и Fj:
Таким образом, выражение суммарной работы от совместного действия обобщённых сил Fi и Fj в случае, когда первой прикладывается сила Fi, а второй Fj, примет вид:
Рассмотрим обратный порядок приложения обобщённых сил: первой приложим статическим способом обобщённую силу Fj, а затем, после её окончательного формирования, – обобщённую силу Fi (рис. 15.1,в). Суммарная работа внешних обобщённых сил Fi и Fj
Учитывая, что Wext,ji = FjDji, получим:
Значение суммарной работы внешних обобщённых сил Fi и Fj не зависит от последовательности их приложения, т.е.
Приняв во внимание соотношения (15.1) и (15.2) окончательно будем иметь: FiDij = FjDjj , или Wext,ij = Wext,ji . (15.3) Выражение (15.3) и составляет содержание теоремы о взаимности возможных работ внешних сил: возможная работа i-й обобщённой силы (внешних сил i-го состояния) на перемещениях, вызванных j-й обобщённой силой (внешними силами j-го состояния), равна возможной работе j-й обобщённой силы (внешних сил j-го состояния) на перемещениях, вызванных i-й обобщённой силой (внешними силами i-го состояния). В строительной механике эта теорема носит имя итальянского учёного Энрико Бетти (1823–1892). Без доказательства отметим справедливость теоремы Бетти для внутренних сил Wint,ij = Wint,ji, т.е. возможная работа внутренних сил i-го состояния на деформациях j-го состояния равна возможной работе внутренних сил j-го состояния на деформациях i-го состояния. Из теоремы Бетти, как частный случай, вытекают другие теоремы взаимности строительной механики, широко используемые в расчётах сооружений. |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 423. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 внешних обобщённых сил будет равна
внешних обобщённых сил будет равна .
. ,
, ,
, .
. . (15.1)
. (15.1) в этом случае запишется:
в этом случае запишется: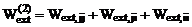 .
. . (15.2)
. (15.2)